Description
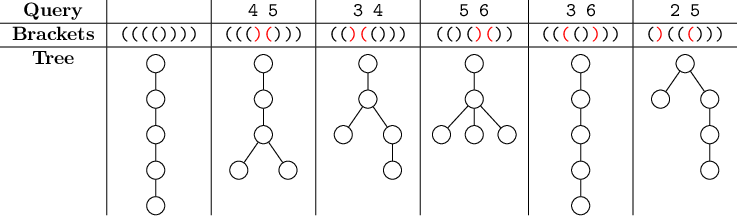
给一个由左右括号组成的正确括号序列(保证一个左括号一定对应右边的一个右括号)。
通过这个括号序列,我们可以构建一棵树:左括号表示进入子树,右括号表示从当前子树返回。括号相当于描述了一棵树先序遍历的出入栈过程。
现在,我们有q次操作。每次操作会交换括号序列中的两个的括号位置,该操作保证括号序列的正确性。每次操作后,都能得到一颗新的树。要求输出最开始和每次操作后树的直径(树上某两点距离的最大值)。
序列代表的树有$n$个节点,操作共$q$次。$3 \leq n \leq 100 000, q \leq100 000$
输出$n+1$棵树的直径
Sample Input & Output
5 5
(((())))
4 5
3 4
5 6
3 6
2 5
4
3
3
2
4
4
Solution
首先考虑到树的子树具有子结构性质。每一步操作都没有完全改变整棵树,有很多子结构的信息是相同的。
那么可以这样思考,在括号序列的任意一个位置开始往后走,我都可以得到一颗与这个位置前面的节点独立的一颗树。这棵树不一定是子树,因为从任意一个位置开始的括号序列可能会多出几个右括号,这种情况下这棵树会往回生长。
再从题目的问题入手,题目要我们求出每颗树的直径来。路径长可以看成两个树的深度减去两倍他们lca的深度。即:设点$u$的深度为$d(u)$,那么$u$到$v$的路径长$l(u, v)=d(u)+d(v)-2\times d(lca(u,v))$。而直径就是所有路径长的最大值。也就是说,如果能得知每个点的深度,并设法维护最大的路径长,就能得到答案。通过括号序列得到每个点每个时刻的深度是很容易的,现在我们就要设法维护路径长,得知路径长又必须知道点对的lca是谁。
恰好,题目给的是树的一个dfs序。任意两点的lca,都是在左边节点之后,右边节点之前访问。那我们也不用管lca是谁了,随便拿$u,v$点中间的一个点$w$,使得$d(u)+d(v)-2\times d(w)$最大的$w$就是它们的lca。即:$l(u, v)=max \{ d(u)+d(v)-2\times d(w) | t_u \leq t_w \leq t_v \}$ ,其中 $t$ 为括号序列中访问节点的时间(也可以说是序列中的下标)。
那问题就变得更简单了。只要是满足 $t_a \leq t_b \leq t_c$ 的三元组 $a,b,c$ ,$d(a) + d(c) - 2 * d(b)$ 就可能是一条路径长。维护最大的这个值,就可以得到直径。
如果只是算一次的话,一边维护当前深度,一边记录下最大的$d(a)$,最小的$d(b)$等值很容易就可以地$O(n)$维护当前直径。但问题是,题目有q次操作。这就得回到开始的分析了——每次操作过后,还有很多子结构的信息保留了下来。
我们需要的是子结构的哪些信息呢?注意到我们计算答案只用到了深度,在每一个子结构代表的树中,我们也必须得维护一些用于计算最大的 $d(a)+d(c)-2\times d(b)$ 的一些深度信息。我们可以把某个子结构开始位置当作相对深度,并记录在这个相对深度下,深度的最大最小值,路径左半边(左边的点到lca距离)的最大值和路径右半边的最大值。同时,还要记录这个子结构的总深度,以得到它和后面一个子结构的相对深度。通过以上信息,就可以维护子结构中最大的 $d(a)+d(c)-2\times d(b)$了。
这种用子结构来解决问题的思想和分治是类似的。分治的每一个结果都可以存在线段树中。虽然第一次求解的复杂度是$O(nlogn)$,但对于每次修改,都能在$O(logn)$的时间里得到新的答案。
总的时间复杂度$O((n + q)logn)$
Review
这道题实际上算法并没有很难,写起来也很容易,但比较考验思维,需要把问题进行巧妙地转换。我一直没有想出解法,是看完官方题解才写出这道题的。虽然我没有自己想出来,但在回味题目巧妙的解法时,还是学到了很多东西的。
在每次操作中,一定是有一些子结构没有改变的。这一点我一直都很清楚,一直都想找出这个子结构。但我一直都拘泥于树的结构,希望先把括号序列转变成树,再找出交换括号是对应树上的把哪一个子树移到哪个地方的操作。这样想下去的话,是怎么也找不出正解的。
想出这道题的关键,应该是想出lca可以用深度表示,而括号序列保证了lca在两点之间。这样的话,求直径就变成了维护几个最大最小值再做计算的问题。这里可以反映出我对树上的一些计算的表达形式还不够熟悉,没有第一时间把求直径的方法转换。而且,我对dfs序的性质不够敏感,没有利用好这个性质。
这样想出了用最大最小值维护答案,怎么建线段树,要维护哪些变量稍微想一想就能想出来。而其中能用线段树维护答案是这道题可以在时限内被解出来的关键。能够用线段树维护子结构,是因为每个路径包含的$a,b,c$三个值的时间是在一个连续区间里的,即$t_a \leq t_b \leq t_c$。这一个序列上的连续性使得问题能够通过线段树来维护。
这也给了我一些启示:线段树不是只能做那些给一个$[l,r]$区间,做一些修改操作的题目的。线段树维护的是连续区间上的性质。如果一个题目中看到了子结构性质,且这些结构构成了连续区间,就可以考虑用线段树来维护。或者换一种想法,如果一个问题可以用连续区间的分治来解决,那么分治的每一步结果就可以用线段树来保存。