我总算找到了博客的正确用法:给自己增加做事情的动力。
寒假回家后,我整个人变得很懒,这个学期最后一门课程的大作业也迟迟没有做完。恰好我发现,自从我把博客链接放到了社交媒体上后,有同学看了我的博客。让别人看到自己“作品”的感觉还是很好的。我打算用写博客的方式来更好地完成作业。
本文按照作业的要求,分为论文概要、代码模块分析、实验结果(使用自己的数据)三个部分。当然,由于我在博客里写东西比较随意,我提交的作业报告肯定会在这篇博客的基础上有所修改。
论文概要
问题定义
本文解决的是一个非常经典的问题:如何恢复一张被模糊和添加噪声的图片。即假设模糊矩阵是$K$,原图像是$u$,噪声是$N$,模糊图像是$g$。那么$g = Ku+N$。现在我们只知道$g$,如何得到$u$。
更具体地,本文介绍的是盲去模糊,即不知道模糊卷积核的情况下,应该如何恢复模糊图像。我上次写的第二个小作业解决的是类似的去模糊问题,但那次问题是一个非盲去模糊,即卷积核已知。
文章贡献
求未知模糊卷积核的问题可以被转换成一个优化问题,即求解某一个损失函数的最小值。文章主要的贡献是提出了一种在损失函数中添加正则化的方法,并且围绕这种方法提供了一套完整的去模糊算法。
方法思想
求解模糊卷积核的优化问题有很多的局部最优解。为了获取一个更好的解,需要加入一些正则化项。正则化项似乎可以用在所有的优化问题里,来避免一些局部最优解。但正则化项的原理我一直都不是很理解,感觉这就是一个被人工设置出来的东西,没有比较清晰的理论依据。把一个参数的正则化项加入优化的损失函数,其直观意义就是让参数不能过大。
在去模糊问题中优化问题中,一般使用的是复原图像的高频图像(后面会详细介绍这个是什么东西)的第一范式(每个分量的和)做为正则化项,加入到需要最小化的损失函数中。该文章发现,噪声增加能让第一范式项也增加,但是模糊却能减少第一范式项。如果单纯地把这一项放进优化目标里,可能得不到好的去模糊效果。文章发现,如果把第一范式和第二范式(每个分量平方和的平方根)的比值做为正则化项的话,无论是模糊增加还是噪声增加,都会让这一项增加。那么,最小化这一项,就能达到同时减少模糊和噪声的效果了。
简而言之,这种新的正则化项较以往的方法,能更好地同时减少噪声和模糊。
算法流程
整体上来看,算法分两步:第一步使用新的优化函数估计出模糊卷积核,这样盲去模糊问题就变成了一个非盲去模糊问题;第二步使用以往的非盲去模糊方法得到去模糊结果。
模糊卷积核估计
卷积核估计是在图像的高频图像进行的。所谓高频图像,就是对图像求x方向的一阶导数和y方向的一阶导数得到的图像。用$y$来表示模糊图像的高频图像,$x$表示修复图像的高频图像,那么优化目标可以写成:
其中$k$是模糊卷积核,$\lambda,\phi$用来调节对应两项的权重。
解决这一优化问题的方法是对两个优化参数$x,k$进行轮流优化。即优化$x$时,假设$k$是一个常量;反之亦然。
更新$x$
此时,优化目标被简化成以下形式:
但这个函数依然是一个没有极点,比较难优化的一个函数。文章中发现,如果第二范式的值固定,即求解
$min_{x} \lambda||Kx-y||_2^2+{||x||_1}$这样一个优化目标的最小值的话,是有一个比较快的iterative shrinkage-thresholding algorithm(ISTA)算法的。
因此,更新$x$又可以分成两层:先在固定第二范式的分母的情况下,使用ISTA更新几次$x$;之后重新计算第二范式,这个大的过程又重复进行几次。
更新$k$
此时,优化目标被简化成以下形式:
这个问题也有现成的算法可以解决。文中用的是无约束的iterative re-weighted least squares (IRLS)算法。
文章中也指出,在实际运用的算法的时候,每次计算出卷积核后要把其中值较小的数直接设为0,以更好应对噪声。
多级卷积核更新优化
由于实际情况中,模糊卷积核可能很大。为了保证卷积核在较大时也能得到一个比较好的解,文章中使用了一种优化方法。该方法从粗到精地计算卷积核,即先假设卷积核很小,使用之前提到的算法计算出卷积核后,再把卷积核细分变大。
在实现时,文章把最开始的卷积核设为3X3,每次以$\sqrt{2}$ 的比例扩大卷积核。对每一层卷积核的更新,$x$和$k$都进行200次交替更新。新一层卷积核使用上一层卷积核的双线性插值得到。
图像恢复
图像恢复用的是Fast image deconvolution using hyper-laplacian priors这篇论文的非盲去模糊方法。该方法大致思想是最小化复原图像做模糊卷积的结果图像和退化图像之间的均方误差。由于非盲去模糊的非适定性较小,不需要再用这篇文章开始提到的第一范数和第二范数的比值做为正则化项。
方法拓展
之前的描述都假设模糊操作是通过一个卷积核来完成的。如果图像因为旋转而扭曲,也可以用类似的方法,只需要修改优化目标中的卷积那一项就行了,大致思想不变。
实验结果与评估
文章首先对Understanding and evaluating blind deconvolution algorithms中提出的4幅用8个大小不同的模糊卷积核得到的32个模糊图片进行去模糊操作,并且用这篇文章中提出的方式来评估去模糊的效果。具体来说,评估的方法是比较还原结果图像与真实图像的均方误差与以已知卷积核还原图像与真实图像的均方误差的比值。这个比值肯定是大于1的,反映的是模糊卷积核复原的效果。文章统计了错误比值的分布(图片错误比值为1、2、3…所占所有图片的百分比)。
文章把新提出的算法与之前的某两个算法进行了比较。
同时,文章还使用了一些现实中的模糊图片实例来进行去模糊。文章还对一些经过旋转扭曲的图像进行复原。这些复原的结果没有经过数据上的评估,但经肉眼观察,这些图像复原的效果还是很好的。
代码模块分析
整体层次
代码的模块调用层次如下:
test_blind_deconv_params(执行算法的函数版本)test_blind_deconv(执行算法的脚本版本)ms_blind_deconv(多级盲去模糊,主函数)ss_blind_deconv(单级估计卷积核、原图像)pcg_kernel_irls_conv(IRLS算法)pcg_kernel_core_irls_conv(IRLS算法中计算一个公式中的值的函数)
fast_deconv_bregman(非盲去模糊算法)solve_image_bregman(解决非盲去模糊中的优化问题的算法)
center_kernel_separate(把卷积核位置调整为居中)
算法接口test_blind_deconv
test_blind_deconv提供了一个对示例图片去模糊的脚本,而test_blind_deconv_params提供了一个接收文件名、模糊卷积核大小的去模糊函数。这两个文件里的内容相同。
算法接口仅仅调用了主去模糊函数ms_blind_deconv,并且默认了一些可调的参数(文件名或模糊图像矩阵,$\lambda$等参数,优化算法循环次数、非盲去模糊的参数等)。
多级盲去模糊主函数ms_blind_deconv
该函数接收文件名和参数结构,返回原图像、模糊图像、模糊卷积核、参数结构。
该函数描述整个算法的主要流程,在调用具体优化算法前对输入图像进行了繁琐的预处理,并最后把去模糊结果显示出来。
和论文中的描述算法流程一样,该函数先对数据预处理,再分级估计卷积核,每一级里先循环更新$x$,再调用IRLS算法更新$k$,求得最终估计模糊卷积核后使用非盲去模糊算法计算复原图像。
预处理部分大致干了以下事情:
- 从文件或参数中读取图像矩阵
- 更改图片的大小
- gamma校正
- RGB转灰度图
- 计算各级卷积核大小
在每一级估计卷积核前,函数还获取初始化卷积核、图像(从上一级插值得来)、计算高频图像。
之后函数调用单级卷积核估计函数ss_blind_deconv。每次卷积核被计算出来后使用center_kernel_separate函数居中卷积核。
最后一级的卷积核被估计出来后,这个卷积核会被存下来。该卷积核用于调用非盲去模糊算法fast_deconv_bregman,最终可以得到去模糊的图像。
单级估计卷积核、原图像ss_blind_deconv
该函数接受模糊图像、初始化复原图像、初始化卷积核、优化函数参数、循环次数,输出复原图像核估计卷积核。
该函数先初始化变量,之后按照论文中的方法,在固定第二范式项的情况下使用ISTA来更新几次$x$,之后更新第二范式项。更新$x$后调用IRLS算法更新$k$。
pcg_kernel_irls_conv函数是IRLS算法。算法中又调用了pcg_kernel_core_irls_conv来计算公式中的一个值。
非盲去模糊算法fast_deconv_bregman
该算法在Fast image deconvolution using hyper-laplacian priors中被提出。算法把最小化损失函数中的可变参数加入x方向的高频图像和y方向的高频图像,在每一轮迭代中使用solve_image_bregman来计算可变参数的更新值。
实验结果
现有数据
使用自带的fishes.jpg
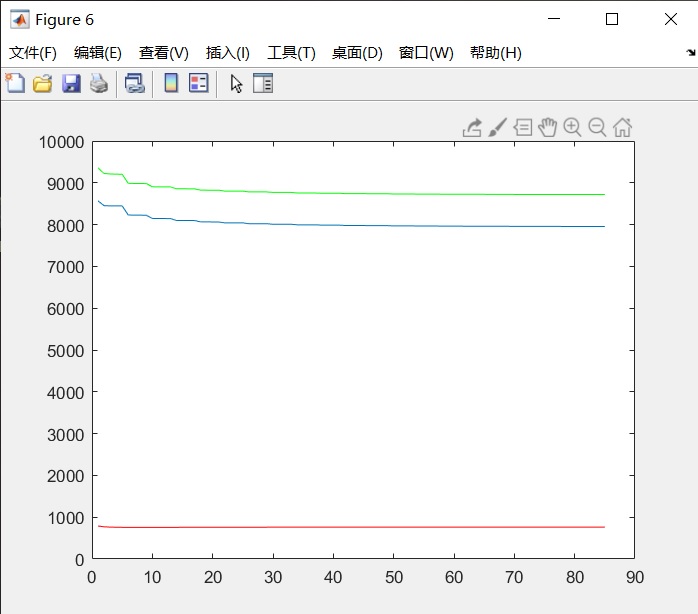
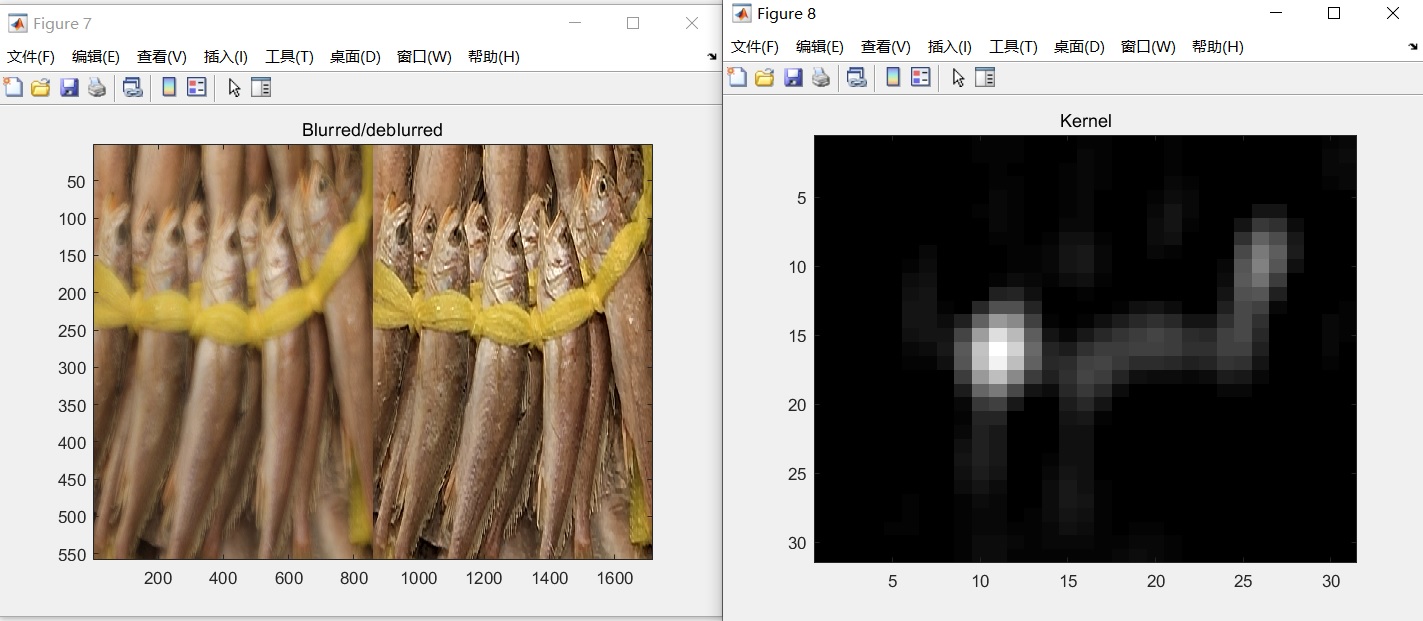
新数据
我使用第二次小作业的模糊图像作为输入,用test_blind_deconv_params("I_n.jpg",9)命令来执行算法。
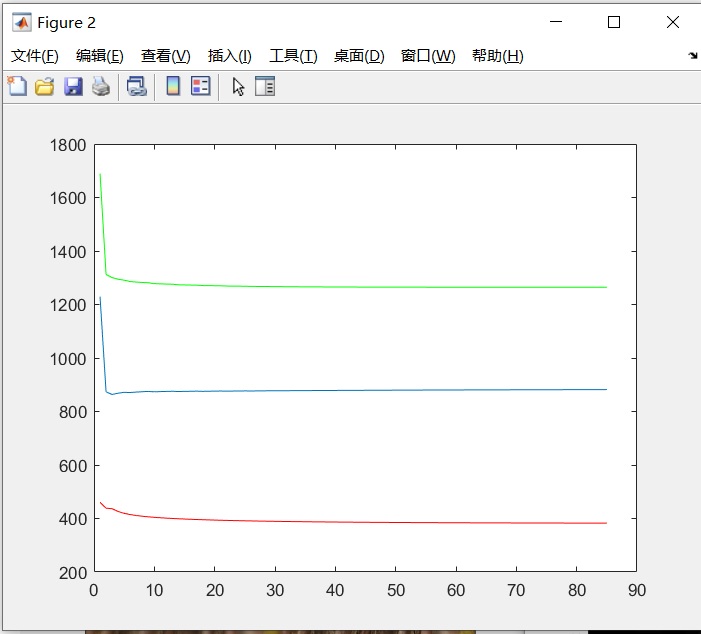
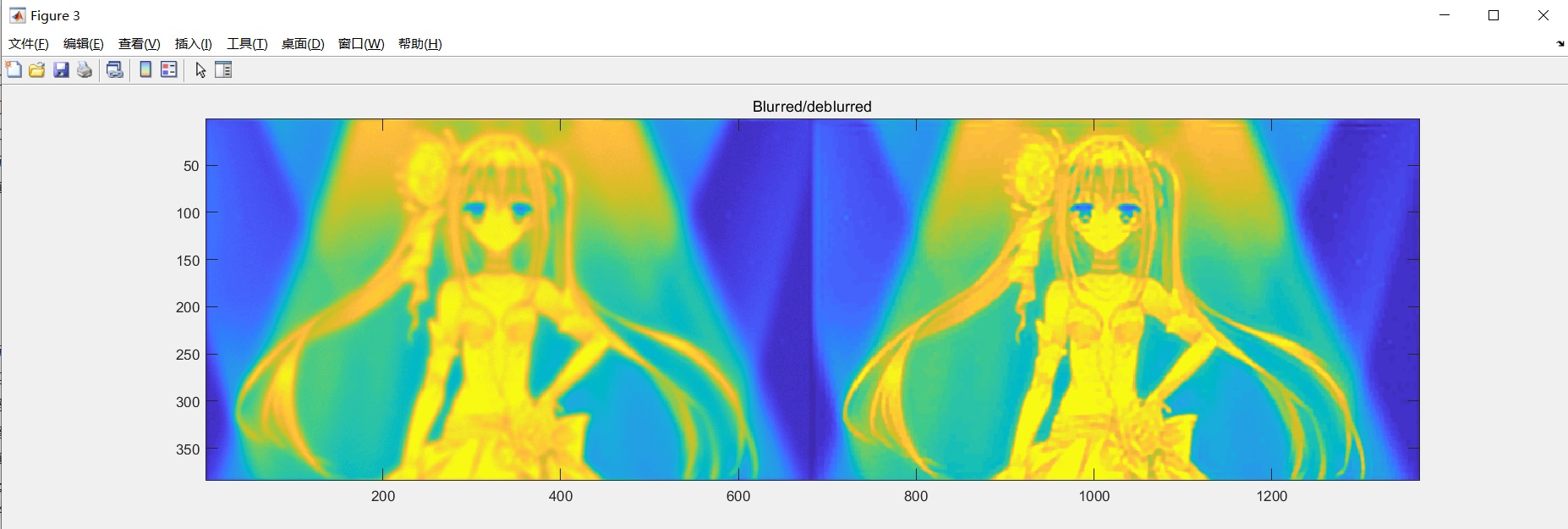
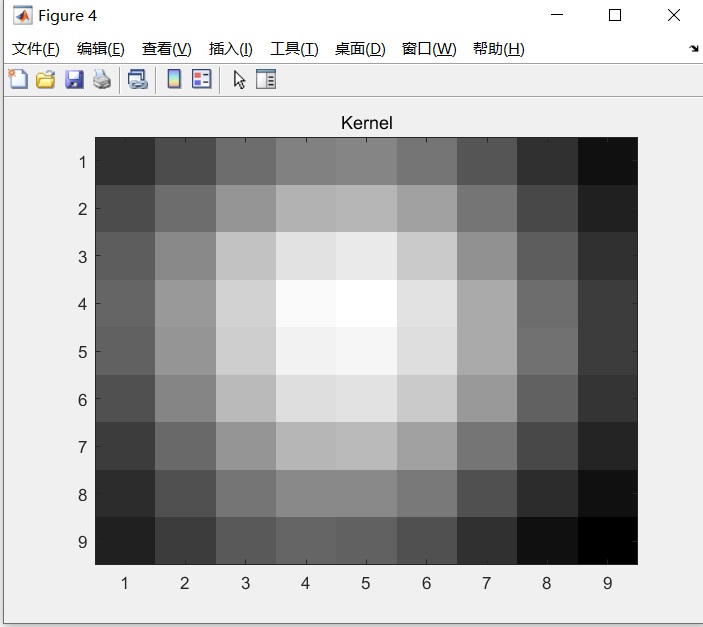
实际的模糊卷积核是一个高斯模糊卷积核。估计的卷积核与真实的卷积核十分接近。