吴恩达《深度学习专项》笔记+代码实战（四）：深层神经网络

体验完了“浅度”神经网络后，我们终于等到了这门课的正题——深度神经网络了。

其实这节课并没有引入太多新的知识，只是把上节课的2层网络拓展成了L层网络。对于编程能力强的同学（或者认真研究了我上节课的编程实战代码的同学，嘿嘿嘿），学完了上节课的内容后，就已经有能力完成这节课的作业了。

课堂笔记

深度神经网络概述与符号标记

所谓深度神经网络，只是神经网络的隐藏层数量比较多而已，它的本质结构和前两课中的神经网络是一样的。让我们再复习一下神经网络中的标记：

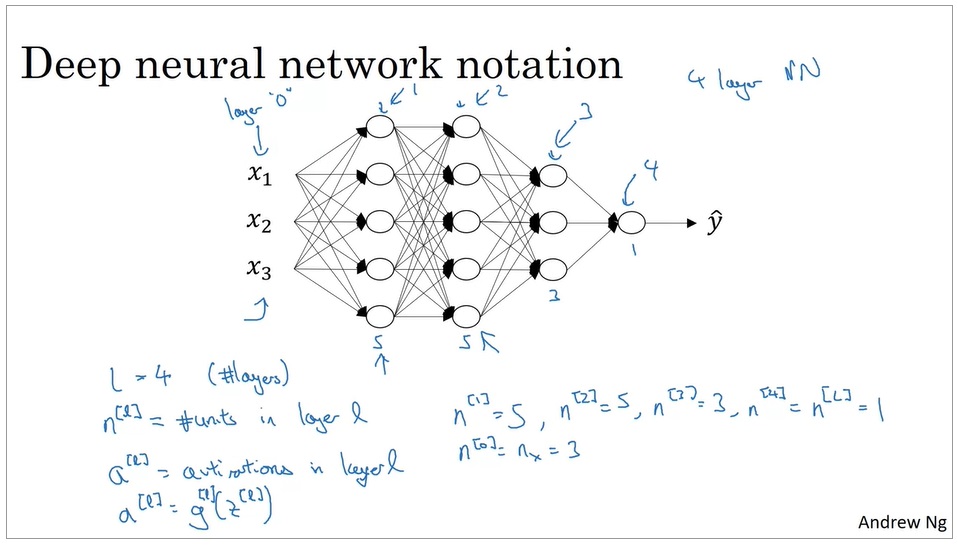
$L$表示网络的层数。

在这个网络中，$L=4$。（注意：输入层并不计入层数，但可以用第“0”层称呼输入层）

上标中括号的标号$l (l \in [0, L])$表示和第$l$层相关的数据。比如, $n^{[l]}$是神经网络第$l$层的神经元数（即每层输出向量的长度）。

这幅图里 $n^{[1]}=5$, $n^{[3]}=3$，以此类推。值得注意的是，$n^{[0]}=n_x=3$。回想第二课的知识，$n_x$是输入向量的长度。

再比如，$a^{[l]}$是第$l$层的输出向量。$a^{[l]}=g^{[l]}(z^{[l]})$，其中$g^{[l]}$是第$l$层的激活函数，$z^{[l]}$是第$l$层的中间运算结果。$W[l], b[l]$是第$l$层的参数。

和上节课的单隐层神经网络类似，对于$L$层的网络，我们如下方法对单样本做前向传播（推理）：

$$\begin{align*} a^{[l]} & \gets g^{[l]}(W^{[l]}a^{[l - 1]}+b^{[l]}) \\ for \ l & \in [1, 2, ... L] \end{align*}$$

其中，输入输出分别为：$x=a^{[0]}, \hat{y}=a^{[L]}$。

当我们考虑全体样本$X, Y$时，上面的算式可以写成：

$$\begin{align*} A^{[l]} & \gets g^{[l]}(W^{[l]}A^{[l - 1]}+b^{[l]}) \\ for \ l & \in [1, 2, ... L] \end{align*}$$

其中，输入输出分别为：$X=A^{[0]}, \hat{Y}=A^{[L]}$。

从公式上看，使用向量化计算全体样本只是把小写字母换成了大写字母而已。用代码实现时，我们甚至也只需要照搬上述公式就行。但我们要记住，全体样本是把每个样本以列向量的形式横向堆叠起来，堆成了一个矩阵。我们心中对$X, Y$的矩阵形状要有数。

在实现深度神经网络时，我们不可避免地引入了一个新的for循环：循环遍历网络的每一层。这个for循环是无法消除的。要记住，我们要消除的for循环，只有向量化计算中的for循环。它们之所以能被消除，是因为向量化计算可以使用并行加速，而不是for循环本身有问题。我们甚至可以把“向量化加法”、“向量化乘法”这些运算视为最小的运算单元。而在写其他代码时，不用刻意去规避for循环。

参数矩阵的形状是：$W^{[l]}: (n^{[l]} , n^{[l-1]}), b^{[l]} : (n^{[l]} , 1)$

每一层的输入输出矩阵形状是：$A^{[l]} : (n^{[l]} , m)$

如果忘了$W$的形状，就拿矩阵乘法形状规则$(a , b) \cdot (b , c)=(a , c)$推一下。

某张量的梯度张量与其形状相同。比如$dW$的形状也是$(n^{[l]} , n^{[l-1]})$。

为什么用更深的网络

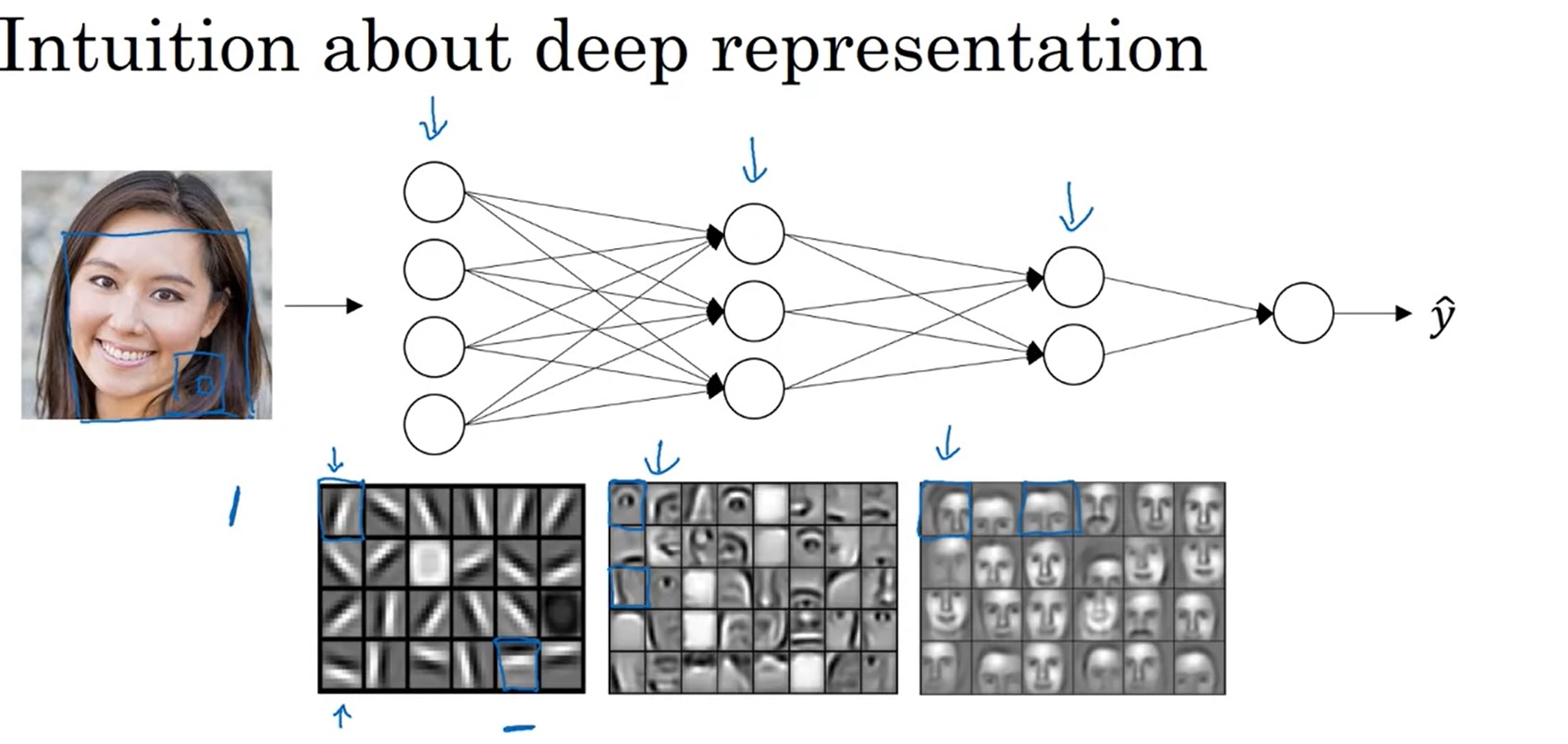
这里给出一种不严谨、出于直觉的解释：网络中越靠前的层，捕捉的信息越初级；越深的层，捕捉的信息越高级。比如对于上图所示的人脸检测网络，网络的第一层可能识别的是图片的边缘，第二层识别的是人的五官，第三层识别的是整个人脸。更深的网络有助于捕捉更高层次的特征。

另外，从计算复杂度的角度来看，用更深的网络，而不是在同一层网络里叠加更多神经元，往往能更轻易地拟合出一个函数。比如要拟合函数a+b+c+d，我们可以先算(a+b)和(c+d)，再算(a+b)+(c+d)。这只需要2“层”计算。如果把上面4个数相加变成$n$个数相加，我们只需要构造$logn$层网络。但如果用单层网络拟合$n$个数相加，网络可能要尝试尝试$a, b, a+b, c, a+b+c, …$这一共$O(2^n)$种公式，需要在1层里放$O(2^n)$个神经元。

这一章反正不是严谨的科学证明，内容听听就好。深度神经网络好不好用，究竟用多少层的网络，这些决定都取决于实际的问题。只不过大多数任务用深度神经网络实现都能生效。

深度神经网络的训练流程

前两节课，我们的网络只有1层或2层。我们或许可以直接写出它们的训练步骤。现在，对于$L$层的网络，我们必须系统化地写出它们的训练流程。

首先是前向传播；

$$\begin{align*} A^{[0]} & = X \\ A^{[1]} & \gets g^{[1]}(Z^{[1]})=g^{[1]}(W^{[1]}A^{[0]}+b^{[1]}) \\ ... & \\ A^{[l]} & \gets g^{[l]}(Z^{[l]})=g^{[l]}(W^{[l]}A^{[l - 1]}+b^{[l]}) \end{align*}$$

在前向传播时，我们要缓存(cache)一些临时变量，以辅助反向传播：

$$\begin{align*} A^{[0]} & = X \\ A^{[1]} & \gets g^{[1]}(Z^{[1]}) \ cache \ A^{[1]}, Z^{[1]},W^{[1]}, b^{[1]} \\ ... & \\ A^{[l]} & \gets g^{[l]}(Z^{[l]}) \ cache \ A^{[l]}, Z^{[l]},W^{[l]}, b^{[l]} \end{align*}$$

反向传播则按下面的步骤计算（注意观察被缓存的变量是怎么使用的）：

$$\begin{align*} dA^{[L]} & = -\frac{y}{a} + \frac{1 - y}{1 - a} \\ ... & \\ dZ^{[l]} & \gets dA^{[l]} \ast g^{[l]'}(Z^{[l]}) &use \ Z^{[l]} \\ dW^{[l]} & \gets \frac{1}{m}dZ^{[l]} A^{[l-1]T} &use \ A^{[l]} \\ db^{[l]} & \gets np.mean(dZ^{[l]}, axis=1, keepdims=True) \\ update & \ W^{[l]}, b^{[l]} &use \ W^{[l]}, b^{[l]}\\ dA^{[l-1]} & \gets W^{[l]T}dZ^{[l]} &use \ W^{[l]} \\ ... \end{align*}$$

上面的公式里，默认损失函数$L(a, y) = -(y loga + (1-y) log(1-a))$

记不住公式没关系，编程的时候对着翻译就行。

从算法的角度来看，梯度下降法只需要用反向传播算法。我们这里之所以做一遍正向传播，是因为反向传播要用到正向传播的中间运算结果。从逻辑关系来看，是反向传播函数调用了正向传播函数，而不是“先正向传播，再反向传播”的并列关系，虽然编程时是用后者来表达。

参数与超参数

之前，我们在不经意间就已经接触了“超参数”这个词，但一直没有对它下一个定义。现在，我们来正式介绍超参数这个概念，以及它和参数的关系。

对于我们之前的神经网络，参数包括：

• $W$
• $b$

这些参数和数学里的参数意义一样，表示函数的参数。

而超参数则包括：

• 学习率 $\alpha$
• 训练迭代次数
• 网络层数 $L$

我们直接从超参数的作用来给超参数下定义。超参数的取值会决定参数$W, b$的取值，它们往往只参与训练，而不参与最后的推理计算。可以说，除了网络中要学习的参数外，网络中剩下的可以变动的数值，都是超参数。

一个简单区别超参数的方法是：超参数一般是我们手动调的。我们常说“调参”，说的是超参数。

吴恩达老师鼓励我们多尝试调参，对于不同的问题可以尝试不同的超参数。

神经网络与大脑

生物的神经由“树突”，“轴突”等部分组成。生物信号会通过这些部分在神经里传播。神经网络的工作原理和生物神经的原理有那么一点类似。

但迄今为止，生物神经的原理还没有被破解。我们把神经网络当成一个$x \to y$的映射就好了。

总结

这一课主要是介绍编程实现的思路，没有过多的知识点：

• 实现任意层数的神经网络
  • 前向传播
  • 反向传播
  • 缓存信息
• 为什么用更深的网络
• 分辨超参数与参数

如果大家对神经网络的前向传播或反向传播还有问题，欢迎去回顾上一篇笔记：https://zhouyifan.net/2022/05/23/DLS-note-3/。

代码实战

说实话，这堂课的编程作业只能称为“体验写代码的感觉”，不能堂堂正正地称为“写程序”。整个框架都搭好了，每行输入输出的变量都给好了，只要填一填函数调用就行了。这样编程实在是不好玩，没有难度，学不到东西。

所以，是时候自己动手写代码了！

两周前，使用逻辑回归做小猫分类并不成功。看看这周换了“深度”神经网络后，我们能不能在小猫分类上取得更好的成绩。

通用分类器类

class BaseRegressionModel(metaclass=abc.ABCMeta):

    def __init__(self):
        pass

    @abc.abstractmethod
    def forward(self, X: np.ndarray, train_mode=True) -> np.ndarray:
        pass

    @abc.abstractmethod
    def backward(self, Y: np.ndarray) -> np.ndarray:
        pass

    @abc.abstractmethod
    def gradient_descent(self, learning_rate: float) -> np.ndarray:
        pass

    @abc.abstractmethod
    def save(self, filename: str):
        pass

    @abc.abstractmethod
    def load(self, filename: str):
        pass

    def loss(self, Y: np.ndarray, Y_hat: np.ndarray) -> np.ndarray:
        return np.mean(-(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)))

    def evaluate(self, X: np.ndarray, Y: np.ndarray, return_loss=False):
        Y_hat = self.forward(X, train_mode=False)
        Y_hat_predict = np.where(Y_hat > 0.5, 1, 0)
        accuracy = np.mean(np.where(Y_hat_predict == Y, 1, 0))
        if return_loss:
            loss = self.loss(Y, Y_hat)
            return accuracy, loss
        else:
            return accuracy

这次我们还是用基于这个通用分类器类编写代码。相比上篇笔记中的代码，这个类有以下改动：

• 由于这次模型要训练很久，我给模型加入了save,load用于保存和读取模型。
• evaluate 不再直接输出结果，而是返回一些评测结果，供调用其的函数使用。注意，这次我们不仅算了测试集上的准确率，还算了测试集上的损失函数。

def train(model: BaseRegressionModel,
          X,
          Y,
          step,
          learning_rate,
          print_interval=100,
          test_X=None,
          test_Y=None):
    for s in range(step):
        Y_hat = model.forward(X)
        model.backward(Y)
        model.gradient_descent(learning_rate)
        if s % print_interval == 0:
            loss = model.loss(Y, Y_hat)
            print(f"Step: {s}")
            print(f"Train loss: {loss}")
            if test_X is not None and test_Y is not None:
                accuracy, loss = model.evaluate(test_X,
                                                test_Y,
                                                return_loss=True)
                print(f"Test loss: {loss}")
                print(f"Test accuracy: {accuracy}")

模型训练的代码和上篇笔记中的也几乎完全相同，只是多输出了一点调试信息。

工具函数

这次我们希望能够更灵活地使用激活函数。因此，我编写了两个根据字符串获取激活函数、激活函数梯度的函数。

def get_activation_func(name):
    if name == 'sigmoid':
        return sigmoid
    elif name == 'relu':
        return relu
    else:
        raise KeyError(f'No such activavtion function {name}')


def get_activation_de_func(name):
    if name == 'sigmoid':
        return sigmoid_de
    elif name == 'relu':
        return relu_de
    else:
        raise KeyError(f'No such activavtion function {name}')

实现任意层数的神经网络

上篇笔记中，我们实现了一个单隐层的神经网络。而这周，我们要实现一个更加通用的神经网络。这个神经网络的层数、每层的神经元数、激活函数都可以修改。还是照着上次的思路，让我们看看这个子类的每个方法是怎么实现的。

class DeepNetwork(BaseRegressionModel):

模型初始化

def __init__(self, neuron_cnt: List[int], activation_func: List[str]):
    assert len(neuron_cnt) - 1 == len(activation_func)
    self.num_layer = len(neuron_cnt) - 1
    self.neuron_cnt = neuron_cnt
    self.activation_func = activation_func
    self.W: List[np.ndarray] = []
    self.b: List[np.ndarray] = []
    for i in range(self.num_layer):
        self.W.append(
            np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) * 0.2)
        self.b.append(np.zeros((neuron_cnt[i + 1], 1)))

我们要在模型初始化时确定模型的结构，因此我们需要刚刚提到的神经网络的层数、每层的神经元数、激活函数这三个信息。在初始化函数中，我们只需要传入每层神经元数的列表、激活函数名的列表即可，神经网络的层数可以通过列表长度来获取。

注意，在构建神经网络时，我们不仅要设置每一层的神经元数，还需要设置输入层的向量长度（回忆一下，输入层虽然不计入网络的层数，但我们还需要根据输入的向量长度设置参数矩阵W的形状）。因此，神经元数列表比激活函数名列表多了一个元素：

assert len(neuron_cnt) - 1 == len(activation_func)

获取了构建模型所需信息（超参数）后，我们按照公式，根据这些信息初始化模型的参数：

for i in range(self.num_layer):
    self.W.append(
        np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) * 0.2)
    self.b.append(np.zeros((neuron_cnt[i + 1], 1)))

别忘了，我们要随机初始化W，且令W为一个较小的值。这里我随便取了个0.2。后面的课程会介绍这个值该怎么设置。

此外，我们还要先准备好缓存的列表：

self.Z_cache = [None] * self.num_layer
self.A_cache = [None] * (self.num_layer + 1)
self.dW_cache = [None] * self.num_layer
self.db_cache = [None] * self.num_layer

由于输入层(A0)的信息也要保留，因此A_cache的长度要多1。

前向传播

回忆这节课提到的前向传播公式：

$$A^{[l]} \gets g^{[l]}(Z^{[l]})=g^{[l]}(W^{[l]}A^{[l - 1]}+b^{[l]}) \\ \ cache \ A^{[l]}, Z^{[l]},W^{[l]}, b^{[l]}$$

我们只需要按照公式做运算并缓存变量即可（下标和公式不完全对应）：

def forward(self, X, train_mode=True):
    if train_mode:
        self.m = X.shape[1]
    A = X
    self.A_cache[0] = A
    for i in range(self.num_layer):
        Z = np.dot(self.W[i], A) + self.b[i]
        A = get_activation_func(self.activation_func[i])(Z)
        if train_mode:
            self.Z_cache[i] = Z
            self.A_cache[i + 1] = A
    return A

注意，虽然公式里写了要缓存模型参数W, b，但实际上在代码实现时，模型参数本来就是类的成员属性，不需要额外去缓存它们。

反向传播

同样，按照公式翻译反向传播即可：

$$\begin{align*} dA^{[L]} & = -\frac{y}{a} + \frac{1 - y}{1 - a} \\ ... & \\ dZ^{[l]} & \gets dA^{[l]} \ast g^{[l]'}(Z^{[l]}) &use \ Z^{[l]} \\ dW^{[l]} & \gets \frac{1}{m}dZ^{[l]} A^{[l-1]T} &use \ A^{[l]} \\ db^{[l]} & \gets np.mean(dZ^{[l]}, axis=1, keepdims=True) \\ dA^{[l-1]} & \gets W^{[l]T}dZ^{[l]} &use \ W^{[l]} \\ ... \end{align*}$$

def backward(self, Y):
    dA = -Y / self.A_cache[-1] + (1 - Y) / (1 - self.A_cache[-1])
    assert (self.m == Y.shape[1])

    for i in range(self.num_layer - 1, -1, -1):
        dZ = dA * get_activation_de_func(self.activation_func[i])(
            self.Z_cache[i])
        dW = np.dot(dZ, self.A_cache[i].T) / self.m
        db = np.mean(dZ, axis=1, keepdims=True)
        dA = np.dot(self.W[i].T, dZ)
        self.dW_cache[i] = dW
        self.db_cache[i] = db

这里除了第一个dA要由误差函数的导数单独算出来外，其他的梯度直接照着公式算就可以了。由于我们把反向传播和更新参数分成了两步，这里额外缓存了dW, db的值。

梯度下降

这次，梯度下降需要循环对所有参数进行：

def gradient_descent(self, learning_rate):
    for i in range(self.num_layer):
        self.W[i] -= learning_rate * self.dW_cache[i]
        self.b[i] -= learning_rate * self.db_cache[i]

存取模型

在介绍存取模型的函数之前，我们要认识两个新的numpy API。

第一个API是np.savez(filename, a_name=a, b_name=b, ...)。它可以把ndarray类型的数据a, b, ...以键值对的形式记录进一个.npz文件中，其中键值对的键是数据的名称，值是数据的值。

第二个API是np.load(filename)。它可以从.npz里读取出一个词典。词典中存储的键值对就是我们刚刚保存的键值对。

比如，我们可以用如下方法存取W, b两个ndarray：

W = np.zeros((1, 1))
b = np.zeros((1, 1))
np.savez('a.npz', W=W, b=b)
params = np.load('a.npz')
assert W == params['W']
assert b == params['b']

学会了这两个API的用法后，我们来看看该怎么存取神经网络的参数：

def save(self, filename: str):
    save_dict = {}
    for i in range(len(self.W)):
        save_dict['W' + str(i)] = self.W[i]
    for i in range(len(self.b)):
        save_dict['b' + str(i)] = self.b[i]
    np.savez(filename, **save_dict)

def load(self, filename: str):
    params = np.load(filename)
    for i in range(len(self.W)):
        self.W[i] = params['W' + str(i)]
    for i in range(len(self.b)):
        self.b[i] = params['b' + str(i)]

和刚刚介绍的用法一样，这里我们要给神经网络中每一个参数取一个独一无二的名字，再把所有名字和值合并成键值对。保存和读取，就是对键值对的写和读。

这里我使用了**save_dict这种传参方式。在Python中，func(**dict)的作用是把一个词典的值当作函数的键值对参数。比如我要写func(a=a, b=b)，我可以定义一个词典d={'a':a, 'b':b}，再用func(**d)把词典传入函数的键值对参数。

小猫分类器

这次，我们还是使用和第二篇笔记中相同的猫狗数据集，作为这次任务的训练集和测试集：

def main():
    train_X, train_Y, test_X, test_Y = get_cat_set(
        'dldemos/LogisticRegression/data/archive/dataset', train_size=1500)
    # train_X: [n_x, m]
    # train_Y: [1, m]

这次我直接在get_cat_set函数里把输入数据的形状调好了，总算不用在main函数看乱糟糟的代码了。

之后，我们根据输入的向量长度，初始化一个较深的神经网络：

n_x = train_X.shape[0]
model = DeepNetwork([n_x, 30, 30, 20, 20, 1],
                    ['relu', 'relu', 'relu', 'relu', 'sigmoid'])

如这段代码所示，我创建了一个有4个隐藏层的神经网络，其中隐藏层的通道数分别为30, 30, 20, 20。除了最后一层用sigmoid以外，每一层都用relu作为激活函数。

初始化完模型后，我们可以开始训练模型了：

model.load('work_dirs/model.npz')
train(model,
      train_X,
      train_Y,
      500,
      learning_rate=0.01,
      print_interval=10,
      test_X=test_X,
      test_Y=test_Y)
model.save('work_dirs/model.npz')

其中，模型是否要读取和保存是可以“灵活地”注释掉的。只需要简单地调用train函数，我们的模型就可以训起来了。

实验结果

本来，写完了代码，讨论实验结果，是一件令人心情愉悦的事情：忙了大半天，总算能看一看自己的成果了。但是，在深度学习项目中，实验其实是最烦人的部分。

如第一课所述，深度学习是一个以实验为主的研究方向，深度学习项目是建立在“实验-开发”这一循环上的。一旦实验效果不佳，你就得去重新调代码。普通的编程项目，你能预计程序有怎样的输出，出了问题你能顺藤摸瓜找到bug。而对于深度学习项目，模型效果不佳，可能是代码有bug，也可能是模型不行。哪怕是知道是模型不行，你也很难确切地知道应该怎么去提升模型。因此，对于深度学习项目，开始实验，仅仅是麻烦的开始。

这不，在开启这周的小猫分类任务实验时，我是满怀期待的：上次用的逻辑回归确实太烂了。这周换了一个这么强大的模型，应该没问题了吧。

结果呢，模型跑了半天，精度还比不过逻辑回归。

我也不好去直接debug啊。我只好对着屏幕大眼瞪小眼，硬生生地用我的人脑编译器去调试代码。

我看了很久，屏幕都快被我眼睛发出的射线射穿了，我还是找不到bug。

我只好断定：这不是代码的问题，是模型或数据的问题。

调了半天超参数后，开始训练。模型用蜗牛般的速度训练了一个小时后，总算达到了 60.5% 的准确率。还好，这个模型没有太丢人，总算比之前逻辑回归的 57.5% 要高上一点点了。

可又过了半小时，这模型的准确率又只有 58.5% 了，准确度就再也上不去了。

这个结果实在是太气人了。相比逻辑回归，这么深的网络竟然只有这么小的提升。

消气后，我冷静地分析了下为什么这个“深度”神经网络的提升这么小：

1. 上次逻辑回归使用的测试集太小，结果不准确。模型可能碰巧多猜对了几次。
2. 还有很多训练优化的手段我没有用上。

还有一些其他方面的原因。现在所有运算都是在CPU上运行的，速度特别慢。如果放到GPU上运算，模型的训练会快上很多。实验速度快了，就有更多的机会去调试模型的超参数，得到更优的模型。

其实，我已经学完了后面几周的课程，知道该怎么优化神经网络的训练；我也知道该怎么在GPU上训练模型。但是，出于教学的考虑，为了让使用的知识尽可能少，我没有提前去使用一些更高级的优化方法和编程手段。我大概只发挥了一成的模型优化水平，使用GPU后实验速度保守估计提升10倍。这样算来，我现在展示的实力，最多只有真实实力的1%。一旦我稍稍拿出5成实力，这个模型的性能就会有显著提升；一旦我释放所有能量，再去多看几篇论文，使用更加优秀的分类模型，那我的模型在这个数据集上的分类精度就可以登顶全球了。只是这样太张扬了不太好。

这样一想，我也没有必要为这个模型的垃圾性能而生气。后面还有的是改进的机会。希望在后面的编程实战中，我们能一点一点见证这个分类模型的提升。

代码链接：https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/DeepNetwork