经过前四周的学习，我们已经学完了《深度学习专项》的第一门课程《神经网络与深度学习》。让我们总结一下这几周学的知识，查缺补漏。

《神经网络与深度学习》知识回顾

概览

在有监督统计机器学习中，我们会得到一个训练集。训练集中的每一条训练样本由输入和输出组成。我们希望构建一个数学模型，使得该模型在学习了训练集中的规律后，能够建立起输入到输出的映射。

在深度学习中，使用的数学模型是深度神经网络。

神经网络一般可以由如下的计算图表示：

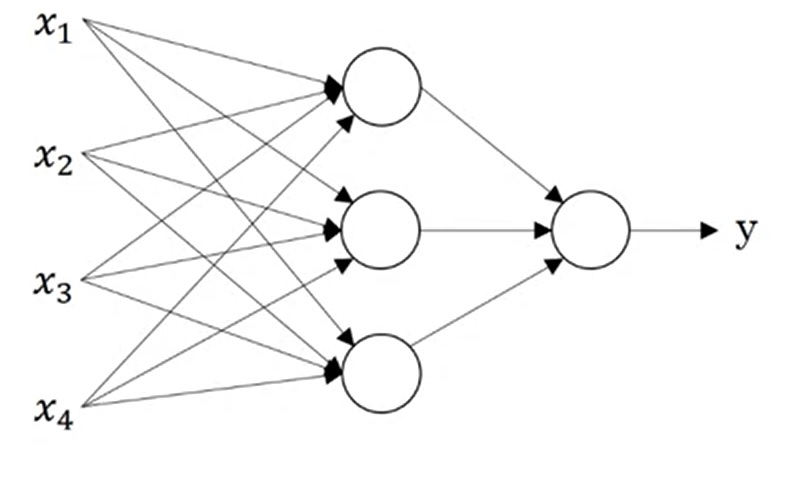
其中，每一个圆形的计算单元（又称神经元）一般表示$g(WX+b)$这一组计算。$W, b$是线性运算的参数，$g$是激活函数。

为了使神经网络学习到输入和正确输出的映射，我们要定义一个描述网络输出和正确输出之间差距的损失函数（即每个样本的网络输出与正确输出的误差函数的平均值），并最小化这个损失函数。这样，网络的“学习”就成为了一个优化问题。

为了对这个优化问题求解，通常的方法是梯度下降法，即通过求导，使每一个参数都沿着让损失函数减少最快的方向移动。

神经网络的结构

神经网络由输入层，隐藏层，输出层组成。计算神经网络的层数$L$时，我们只考虑隐藏层与输出层。

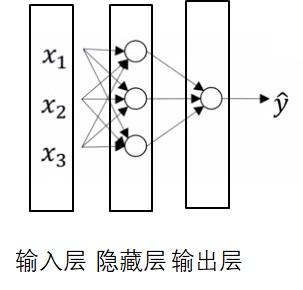
令$x^{(i)[j]}_k$表示某向量在第$i$个样本第$j$层的第$k$个分量。

若每层的神经元个数为$n^{[l]}$，特别地，令输入的通道数$n_x=n^{[0]}$，则每层参数的形状满足$W^{[l]}:(n^{[l]}, n^{[l-1]})$，$b^{[l]}:(n^{[l]}, 1)$。

常见的激活函数有sigmoid, tanh, relu, leaky_relu。一般隐藏层的激活函数$g^{[l]}(l < L)$用relu。对于二分类问题（输出为0或1），输出层的激活函数$g^{[L]}$应用sigmoid。

神经网络的训练

初始化参数：随机初始化$W$并使其绝对值较小，用零初始化$b$。

重复执行以下步骤：

前向传播：直接运行神经网络，并缓存中间计算结果$A, Z$。
反向传播：倒着“运行”神经网络，根据求导链式法则，由网络输出求得每一个参数的导数。
梯度下降：对于每个参数$p = w^{[l]} or b^{[l]}$，用$p := p-\alpha dp$更新参数。其中$\alpha$叫学习率，表示参数更新的速度。

用numpy实现神经网络

把输入图片进行“压平”操作：

1	images = np.reshape(images, (-1))

初始化参数

1 2	W = np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) * 0.01 b = np.zeros((neuron_cnt[i + 1], 1))

前向传播

self.A_cache[0] = A
for i in range(self.num_layer):
    Z = np.dot(self.W[i], A) + self.b[i]
    A = get_activation_func(self.activation_func[i])(Z)
    if train_mode:
        self.Z_cache[i] = Z
        self.A_cache[i + 1] = A

反向传播

for i in range(self.num_layer - 1, -1, -1):
    dZ = dA * get_activation_de_func(self.activation_func[i])(
        self.Z_cache[i])
    dW = np.dot(dZ, self.A_cache[i].T) / self.m
    db = np.mean(dZ, axis=1, keepdims=True)
    dA = np.dot(self.W[i].T, dZ)
    self.dW_cache[i] = dW
    self.db_cache[i] = db

梯度下降

1
2
3

for i in range(self.num_layer):
    self.W[i] -= learning_rate * self.dW_cache[i]
    self.b[i] -= learning_rate * self.db_cache[i]

第一阶段学习情况自评

学了几周，大家可能不太清楚自己现在的水平怎么样了。这里，我给大家提供了一个用于自我评价的标准，大家可以看看自己现在身处第几层。

Level 1 能谈论深度学习的程度

知道深度学习能解决计算机视觉、自然语言处理等问题。
能够说出“训练集”、“神经网络”等专有名词

Level 2 能调用深度学习框架的程度

知道正向传播、反向传播、梯度下降的意义。
虽然现在不会用代码实现学习算法，但通过后面的学习，能够用深度学习框架编写学习算法。

Level 3 掌握所有知识细节的程度

反向传播的流程。
为什么必须使用激活函数。
为什么要随机初始化参数。
正向传播时为什么要缓存，缓存的变量在反向传播时是怎么使用的。

Level 4 能从零开始实现一个分类器的程度

升级语音：别说是用numpy，就算是用纯C++，我也能造一个神经网络！

掌握 numpy 的基本操作。
能用 Python 编写一个神经网络框架。
能用 numpy 实现神经网络的计算细节。
能用 Python 实现读取数据集、输出精度等繁杂的操作。

第二阶段知识预览

《深度学习专项》第二门课的标题是《改进深度神经网络：调整超参数、正则化和优化》。从标题中也能看出，这门课会介绍广泛的改进深度神经网络性能的技术。具体来说，在三周的时间里，我们会学习：

第一周：深度学习的实践层面
- 训练集/开发集/测试集的划分
- 偏差与方差
- 机器学习的基础改进流程
- 正则化
- 输入归一化
- 梯度问题与加权初始化
- 梯度检查
第二周：优化算法
- 分批梯度下降
- 更高级的梯度下降算法
- 学习率衰减
第三周：调整超参数、批归一化和编程框架
- 调参策略
- 批归一化
- 多分类问题
- 深度学习框架 TensorFlow

目录还是比较凌乱的，让我们具体看一下每项主要知识点的介绍：

训练集/开发集/测试集的划分
- 之前我们只把数据集划分成训练集和测试集两个部分。但实际上，我们还需要一个用于调试的“开发集”。
偏差与方差
- 机器学习模型的性能不够好，体现在高偏差和高方差两个方面。前者表示模型的描述能力不足，后者表示模型在训练集上过拟合。
- 为了解决过拟合问题，我们要使用添加正则项、dropout等正则化方法。
梯度问题
- 在较深的神经网络中，数值运算结果可能会过大或过小，这会导致梯度爆炸或者梯度弥散。
- 加权初始化可以解决这一问题。我们即将认识多种初始化参数的方法。
优化梯度下降
- 使用mini-batch：处理完部分训练数据后就执行梯度下降，而不用等处理完整个训练数据集。
- 使用更高级的梯度下降算法，比如让梯度更平滑的momentum优化器，以及结合了多种算法的adam优化器。
- 在训练一段时间后，减少学习率也能提高网络的收敛速度。
调参策略
- 在调试神经网络的超参数时，有一些超参数的优先级更高。我们应该按照优先级从高到低的顺序调参。
- 在调参时，一种技巧是多次随机选取超参数，观察哪些配置下网络的表现最好。
归一化
- 对输入做归一化能够加速梯度下降。
- 除了对输入做归一化外，我们还可以对每一层的输出做批归一化，这项技术能够让我们的网络更加健壮。
多分类问题
- 前几周我们一直关注的是二分类问题。我们将学习如何用类似的公式，把二分类问题推广到多分类问题。
编程框架
- 深度学习编程框架往往带有自动求导的功能，能够极大提升我们的开发效率。学完第二门课后，我们将一直使用TensorFlow来编程。
- 我会顺便介绍所有编程任务的 PyTorch 等价实现。

可以看出，第二门课包含的内容非常多。甚至很多知识都只会在课堂上提一两句，得通过阅读原论文才能彻底学会这些知识。但是，这门课的知识都非常重要。学完了第二门课后，我们对于深度学习的理解能提升整整一个台阶。让我们做好准备，迎接下周的学习。

关注我社交媒体的人，肯定质疑我最近的行为：你最近怎么发文章只注意数量不注意质量啊？怎么一篇文章可以拆开来发好几遍啊？

这你就不懂了。我最近想看看，这些社交平台究竟有多捞：我提供了这么优质的文字内容，我看你们会不会去认真推广，会不会发掘优质内容。结果，我发现这些平台确实都很捞，根本不去好好推送的。没办法，我只好先写一批质量中等的文章，增加发文的次数。我倒要看看这些平台什么时候能给我符合我文章质量的关注量。文章看的人多，我才有继续创作更优质内容的动力。

周弈帆的博客

吴恩达《深度学习专项》第一阶段总结与第二阶段预览