吴恩达《深度学习专项》笔记+代码实战（六）：改进梯度下降算法

学习提示

一直以来，我们都用梯度下降法作为神经网络的优化算法。但是，这个优化算法还有很多的改进空间。这周，我们将学习一些更高级的优化技术，希望能够从各个方面改进普通的梯度下降算法。

我们要学习的改进技术有三大项：分批梯度下降、高级更新方法、学习率衰减。这三项是平行的，可以同时使用。

分批梯度下降是从数据集的角度改进梯度下降。我们没必要等遍历完了整个数据集后再进行参数更新，而是可以遍历完一小批数据后就进行更新。

高级更新方法指不使用参数的梯度值，而是使用一些和梯度相关的中间结果来更新参数。通过使用这些更高级的优化算法，我们能够令参数的更新更加平滑，更加容易收敛到最优值。这些高级的算法包括gradient descent with momentum, RMSProp, Adam。其中Adam是前两种算法的结合版，这是目前最流行的优化器之一。

学习率衰减指的是随着训练的进行，我们可以想办法减小学习率的值，从而减少参数的震荡，令参数更快地靠近最优值。

在这周的课里，我们要更关注每种优化算法的单独、组合使用方法，以及应该在什么场合用什么算法，最后再去关注算法的实现原理。对于多数技术，“会用”一般要优先于“会写”。

课堂笔记

分批梯度下降

这项技术的英文名称取得极其糟糕。之前我们使用的方法被称为”batch gradient descent”, 改进后的方法被称为”mini-batch gradient descent”。但是，这两种方法的本质区别是是否把整个数据集分成多个子集。因此，我们认为我的中文翻译“分批梯度下降”、“整批梯度下降”比原来的英文名词或者“小批量梯度下降”等中文翻译要更贴切名词本身的意思。

使用mini-batch

在之前的学习中，我们都是用整个训练集的平均梯度来更新模型参数的。而如果训练集特别大的话，遍历整个数据集要花很长时间，梯度下降的速度将十分缓慢。

其实，我们不一定要等遍历完了整个数据集再做梯度下降。相较于每次遍历完所有$m$个训练样本再更新，我们可以遍历完一小批次(mini-batch)的样本就更新。让我们来看课件里的一个例子：

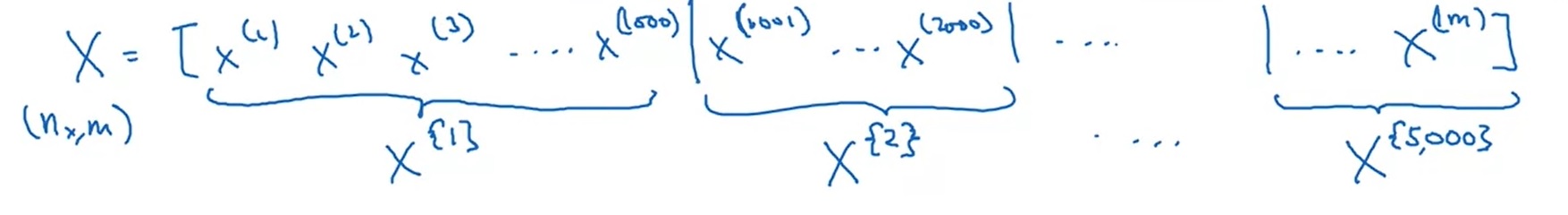
假设整个数据集大小$m=5,000,000$。我们可以把数据集划分成5000个mini-batch，其中每一个batch包含1000个数据。做梯度下降时，我们每跑完一个batch里的1000个数据，就用它们的平均梯度去更新参数，再去跑下一个batch。

这里要介绍一个新的标记。设整个数据集$X$的形状是$(n_x, m)(m=5,000,000)$，则第$i$个数据集的标记为 $X^{\lbrace i \rbrace}$ ,形状为$(n_x, 1000)$。

再次总结一下标记：$x^{(i)[j]\lbrace k\rbrace}$中的上标分别表示和第i个样本相关、和第j层相关、和第k个批次的样本集相关。实际上这三个标记几乎不会同时出现。

使用了分批梯度下降后，算法的写法由

for i in range(m):
    update parameters

变成

for i in range(m / batch_size)
  for j in range(batch_size):
      update parameters

。现在的梯度下降法每进行一次内层循环，就更新一次参数。我们还是把一次内层循环称为一个”step（步）”。此外，我们把一次外层循环称为一个”epoch(直译为’时代’，简称‘代’)”，因为每完成一次外层循环就意味着训练集被遍历了一次。

mini-batch 的损失函数变化趋势

使用分批梯度下降后，损失函数的变化趋势会有所不同:

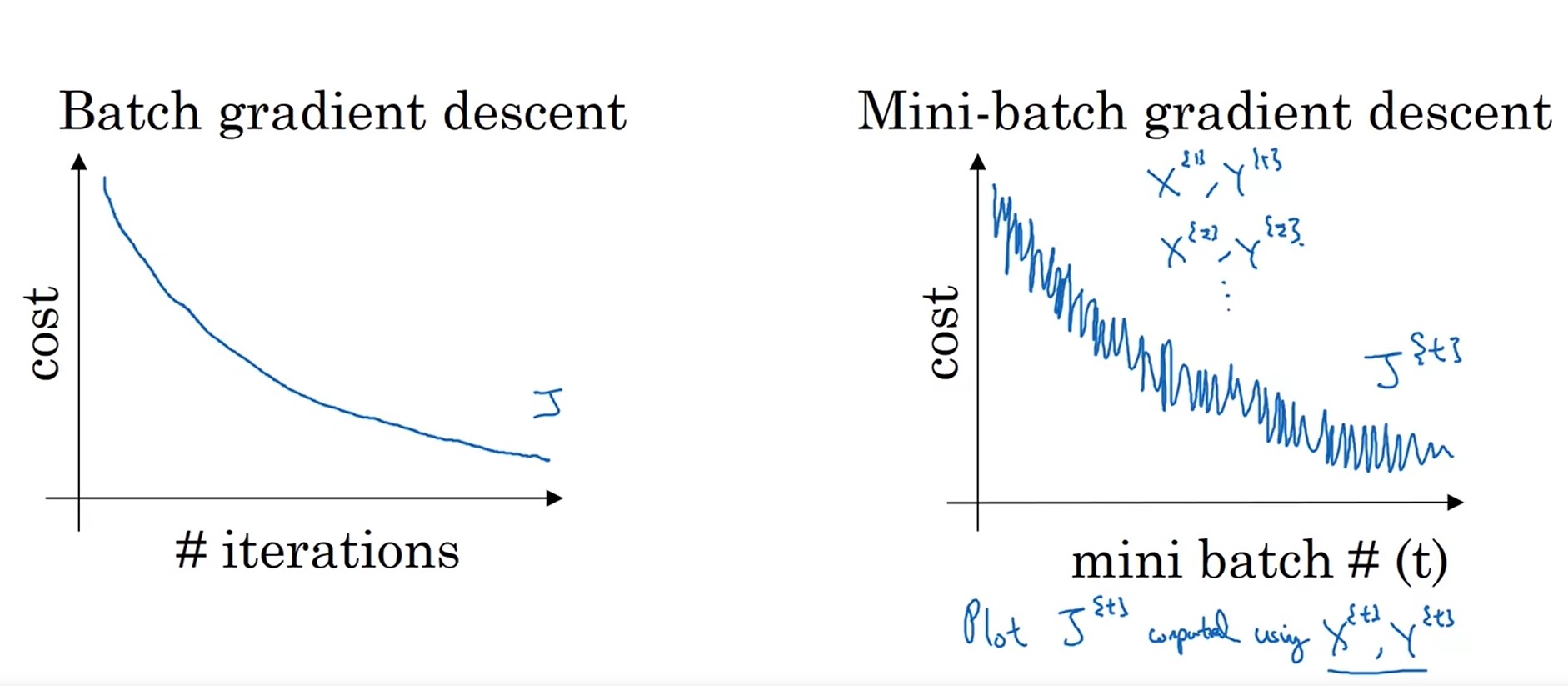
如图所示，如果是使用整批梯度下降，则损失函数会一直下降。但是，使用分批梯度下降后，损失函数可能会时升时降，但总体趋势保持下降。

这种现象主要是因为之前我们计算的是整个训练集的损失函数，而现在计算的是每个mini-batch的损失函数。每个mini-batch的损失函数时高时低，可以理解为：某批数据比较简单，损失函数较低；另一批数据难度较大，损失函数较大。

选择批次大小

批次大小(batch size)对训练速度有很大的影响。

如果批次过大，甚至极端情况下batch_size=m，那么这等价于整批梯度下降。我们刚刚也学过了，如果数据集过大，整批梯度下降是很慢的。

如果批次过小，甚至小到batch_size=1（这种梯度下降法有一个特别的名字：随机梯度下降（Stochastic Gradient Descent）），那么这种计算方法又会失去向量化计算带来的加速效果。

回想一下第二周的内容：向量化计算指的是一次对多个数据做加法、乘法等运算。这种计算方式比用循环对每个数据做计算要快。

出于折中的考虑，我们一般会选用一个介于1-m之间的数作为批次大小。

如果数据集过小(m<2000)，那就没必要使用分批梯度下降，直接拿整个数据集做整批梯度下降即可。

如果数据集再大一点，就可以考虑使用64, 128, 256, 512这些数作为batch_size。这几个数都是2的次幂。由于电脑的硬件容量经常和2的次幂相关，把batch_size恰好设成2的次幂往往能提速。

当然，刚刚也讲了，使用较大batch_size的一个目的是充分利用向量化计算。而向量化计算要求参与运算的数据全部在CPU/GPU内存上。如果设备的内存不够，则设过大的batch_size也没有意义。

一段数据的平均值

在课堂上，这段内容是从数学的角度切入介绍的。我认为这种介绍方式比较突兀。我将从计算机科学的角度切入，用更好理解的方式介绍“指数加权移动平均”。

背景

假设我们绘制了某年每日气温的散点图：

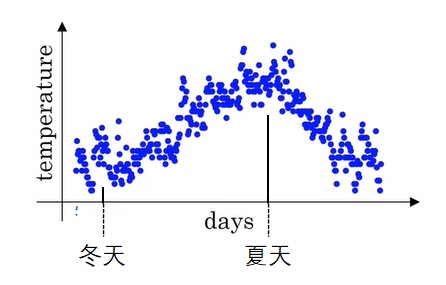
假如让你来描述全年气温的趋势，你会怎么描述呢？

作为人类，我们肯定会说：“这一年里，冬天的气温较低。随后气温逐渐升高，在夏天来到最高值。夏天过后，气温又逐渐下降，直至冬天的最低值。”

但是，要让计算机看懂天气的变化趋势，应该怎么办呢？直接拿相邻的天气的差作为趋势可不行。冬天也会出现第二天气温突然升高的情况，夏天也会出现第二天气温突然降低的情况。我们需要一个能够概括一段时间内气温情况的指标。

移动平均数

一段时间里的值，其实就是几天内多个值的总体情况。多个值的总体情况，可以用平均数表示。严谨地来说，假如这一年有365天，我们用$t$表示这一年每天的天气，那么：

$$t_i=\left\{ \begin{aligned} &第i天的天气 &(1 \leq i \leq 365) \\ &0 &(i取其他值) \end{aligned} \right.$$

我们可以定义一种叫做移动平均数(Moving Averages) 的指标，表示某天及其前几天温度的平均值。比如对于5天移动平均数$ma$，其定义如下：

$$ma_i=\frac{t_i+t_{i-1}+t_{i-2}+t_{i-3}+t_{i-4}}{5} (1 \leq i \leq 365)$$

假如要让计算机依次输出每天的移动平均数，该怎么编写算法呢？我们来看几个移动平均数的例子：

$$\begin{aligned} ma_5=(t_5+t_4+t_3+t_2+t_1)/5 \\ ma_6=(t_6+t_5+t_4+t_3+t_2)/5 \\ ma_7=(t_7+t_6+t_5+t_4+t_3)/5 \end{aligned}$$

通过观察，我们可以发现$ma_6=ma_5+(t_6-t_1)/5$，$ma_7=ma_6+(t_7-t_2)/5$。

也就是说，在算n天里的m天移动平均数（我们刚刚计算的是5天移动平均数）时，我们不用在n次的外层循环里再写一个m次的循环，只需要根据前一天的移动平均数，减一个值加一个值即可。这种依次输出移动平均数的算法如下：

input temperature[0:n]
input m

def get_temperature(i):
    return temperature[i] if i >= 0 and i < n else 0

ma = 0
for i in range(n):
    ma += (get_temperature(i) - get_temperature(i - m)) / m
    ma_i = ma
    output ma_i

这种求移动平均数的方法确实很高效。但是，我们上面这个算法是基于所有温度值一次性给出的情况。假如我们正在算今年每天温度的移动平均数，每天的温度是一天一天给出的，而不是一次性给出的，上面的算法应该怎么修改呢？让我们来看修改后的算法：

input m
temp_i_day_ago = zeros((m))

def update_temperature(t):
    for i in range(m - 1):
        temp_i_day_ago[i+1] = temp_i_day_ago[i]
    temp_i_day_ago[0] = t

ma = 0
for i in range(n):
    input t_i
    update_temperature(t_i)
    ma += (temp_i_day_ago[0] - temp_i_day_ago[m]) / m
    ma_i = ma
    output ma_i

由于我们不能提前知道每天的天气，我们需要一个大小为m的数组temp_i_day_ago记录前几天的天气，以计算m天移动平均数。

上述代码的时间复杂度还是有优化空间的。可以用更好的写法去掉update_temperature里的循环，把计算每天移动平均数的时间复杂度变为$O(1)$。但是，这份代码的空间复杂度是无法优化的。为了算m天移动平均数，我们必须要维护一个长度为m的数组，空间复杂度一定是$O(m)$。

对于一个变量的m移动平均数，$O(m)$的空间复杂度还算不大。但假如我们要同时维护l个变量的m移动平均数，整个算法的空间复杂度就是$O(ml)$。在l很大的情况下，m对空间的影响是很大的。哪怕m取5这种很小的数，也意味着要多花4倍的空间去存储额外的数据。空间复杂度里这多出来的这个$m$是不能接受的。

指数加权移动平均

作为移动平均数的替代，人们提出了指数加权移动平均数（Exponential Weighted Moving Average） 这种表示一段时期内数据平均值的指标。其计算公式为：

$$v_i=\beta v_{i-1} + (1 - \beta)t_i$$

这个公式直观上的意义为：一段时间内的平均温度，等于上一段时间的平均温度与当日温度的加权和。

相比普通的移动平均数，指数平均数最大的好处就是减小了空间复杂度。在迭代更新这个新的移动平均数时，我们只需要维护一个当前平均数$v_i$，一个当前的温度$t_i$即可，空间复杂度为$O(1)$。

让我们进一步理解公式中的参数$\beta$。把公式展开可得：

$$\begin{aligned} v_i&=(1 - \beta)t_i + \beta v_{i-1} \\ v_i&=(1 - \beta)t_i + (1 - \beta)\beta t_{i-1} +\beta^2 v_{i-2} \\ v_i&=(1 - \beta)t_i + (1 - \beta)\beta t_{i-1} + (1 - \beta)\beta ^2t_{i-2}+ \beta^3 v_{i-2} \\ ... \end{aligned}$$

从这个式子可以看出，之前数据的权重都在以$\beta$的速度指数衰减。根据$(1-\epsilon)^{\frac{1}{\epsilon}} \approx \frac{1}{e}$，并且我们可以认为一个数到了$\frac{1}{e}$就小到可以忽视了，那么指数平均数表示的就是$\frac{1}{1-\beta}$天内数据的平均情况。比如$\beta=0.9$表示的是10天内的平均数据，$\beta=0.99$表示的是100天内的平均数据。

偏差矫正

指数平均数存在一个问题。在刚刚初始化时，指数平均数的值可能不太正确，请看：

$$\begin{aligned} v_1 &= (1 - \beta)t_1 \\ v_2 &= (1 - \beta)\beta t_1 +(1 - \beta)t_2 \end{aligned}$$

让我们把每一项前面的权重加起来。对于$v_1$，前面的权重和是$(1-\beta)$；对于$v_2$，前面的权重和是$(1-\beta)(\beta+1)$。显然，这两个权重和都不为1。而计算平均数时，我们希望所有数据的权重和为1，这样才能反映出数据的真实大小情况。这里出现了权重上的“偏差”。

为了矫正这个偏差，我们应该想办法把权重和矫正为1。观察刚才的算式可以发现，第$i$项的权重和如下：

$$w_i = (1-\beta)(1+\beta+\beta^2+...\beta^i)$$

根据等比数列求和公式，上式化简为：

$$\begin{aligned} w_i &= (1-\beta)\frac{(1-\beta^i)}{(1-\beta)} \\ w_i &= 1-\beta^i \end{aligned}$$

为了令权重和为1，我们可以令每一项指数平均数都除以这个和，即用下面的式子计算矫正后的指数平均数$v_i’$:

$$v_i'=\frac{v_i}{1-\beta^i}$$

但是，在实践中，由于这个和$1-\beta^i$收敛得很快，我们不会特地写代码做这个矫正。

Momentum

Gradient Descent with Momentum (使用动量的梯度下降) 是一种利用梯度的指数加权移动平均数更新参数的策略。在每次更新学习率时，我们不用本轮梯度的方向作为梯度下降的方向，而是用梯度的指数加权移动平均数作为梯度下降的方向。即对于每个参数，我们用下式做梯度下降：

$$\begin{aligned} V_{dw}&=\beta V_{dw}+ (1-\beta)dw \\ V_{db}&=\beta V_{db}+ (1-\beta)db \\ w &:= w - \alpha V_{dw} \\ b &:= b - \alpha V_{db} \end{aligned}$$

也就是说，对于每个参数$p$，我们用它的指数平均值$v_{dp}$代替$dp$进行参数的更新。

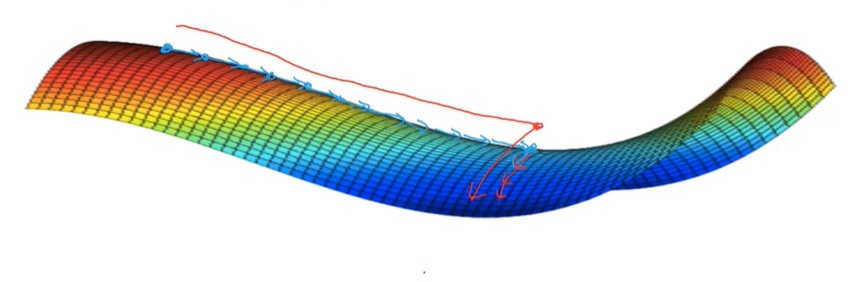
使用梯度的平均值来更新有什么好处呢？让我们来看一个可视化的例子：

不使用 Momentum 的话，每次参数更新的方向可能变化幅度较大，如上图中的蓝线所示。而使用 Momentum 后，每次参数的更新方向都会在之前的方向上稍作修改，每次的更新方向会更加平缓一点，如上图的红线所示。这样，梯度下降算法可以更快地找到最低点。

在实现时，我们不用去使用偏差矫正。$\beta$取0.9在大多数情况下都适用，有余力的话这个参数也可以调一下。

RMSProp 和 Adam

课堂上并没有对RMSProp的原理做过多的介绍，我们只需要记住它的公式就行。我会在其他文章中介绍这几项技术的原理。

在一个神经网络中，不同的参数需要的更新幅度可能不一样。但是，在默认情况下，所有参数的更新幅度都是一样的（即学习率）。为了平衡各个参数的更新幅度，RMSProp(Root Mean Squared Propagation) 在参数更新公式中添加了一个和参数大小相关的权重$S$。与 Momentum 类似，RMSProp使用了某种移动平均值来平滑这个权重的更新。其梯度下降公式如下：

$$\begin{aligned} S_{dw}&=\beta S_{dw}+ (1-\beta)dw^2 \\ S_{db}&=\beta S_{db}+ (1-\beta)db^2 \\ w &:= w - \alpha \frac{dw}{\sqrt{S_{dw}}} \\ b &:= b - \alpha \frac{db}{\sqrt{S_{db}}} \end{aligned}$$

在编程实现时，我们应该给分母加一个极小值$\epsilon$，防止分母出现0。

Adam (Adaptive Moment Estimation) 是 Momentum 与 RMSProp 的结合版。为了使用Adam，我们要先计算 Momentum 和 RMSProp 的中间变量：

$$\begin{aligned} V_{dw}&=\beta_1 V_{dw}+ (1-\beta_1)dw \\ V_{db}&=\beta_1 V_{db}+ (1-\beta_1)db \\ S_{dw}&=\beta_2 S_{dw}+ (1-\beta_2)dw^2 \\ S_{db}&=\beta_2 S_{db}+ (1-\beta_2)db^2 \end{aligned}$$

之后，根据前面的偏差矫正，获得这几个变量的矫正值：

如前文所述，在实现时添加偏差矫正意义不大。估计这里加上偏差矫正是因为原论文加了。

$$\begin{aligned} V_{dw}'&=\frac{V_{dw}}{1-\beta_1^t} \\ V_{db}'&=\frac{V_{db}}{1-\beta_1^t} \\ S_{dw}'&=\frac{S_{dw}}{1-\beta_2^t} \\ S_{db}'&=\frac{S_{db}}{1-\beta_2^t} \\ \end{aligned}$$

最后，进行参数的更新：

$$\begin{aligned} w &:= w - \alpha \frac{V_{dw}'}{\sqrt{S_{dw}'}+\epsilon} \\ b &:= b - \alpha \frac{V_{db}'}{\sqrt{S_{db}'}+\epsilon} \end{aligned}$$

和之前一样，这里的$\epsilon$是一个极小值。在编程时添加$\epsilon$，一般都是为了防止分母中出现0。

Adam是目前非常流行的优化算法，它的表现通常都很优秀。为了用好这个优化算法，我们要知道它的超参数该怎么调。在原论文中，这个算法的超参数取值如下：

$$\begin{aligned} \beta_1 &= 0.9 \\ \beta_2 &= 0.999 \\ \epsilon &= 10^{-8} \end{aligned}$$

绝大多数情况下，我们不用手动调这三个超参数。

学习率衰减

训练时的学习率不应该是一成不变的。在优化刚开始时，参数离最优值还差很远，选较大的学习率能加快学习速度。但是，经过了一段时间的学习后，参数离最优值已经比较近了。这时，较大的学习率可能会让参数错过最优值。因此，在训练一段时间后，减小学习率往往能够加快网络的收敛速度。这种训练一段时间后减小学习率的方法叫做学习率衰减。

其实学习率衰减只是一种比较宏观的训练策略，并没有绝对正确的学习率衰减方法。我们可以设置初始学习率$\alpha_0$，之后按下面的公式进行学习率衰减：

$$\alpha = \frac{1}{1 + DecayRate \ast EpochNum}\alpha_0$$

这个公式非常简单，初始学习率会随着一个衰减率(DecayRate)和训练次数(EpochNum)衰减。

同样，我们还可以使用指数衰减：

$$\alpha = 0.95^{EpochNum}\alpha_0$$

或者其他一些奇奇怪怪的衰减方法(k是超参数）：

$$\alpha = \frac{k}{\sqrt{EpochNum}}\alpha_0$$

甚至我们可以手动调学习率，每训练一段时间就把学习率调整成一个更小的常数。

总之，学习率衰减是一条启发性的规则。我们可以有意识地在训练中后期调小学习率。

局部最优值

在执行梯度下降算法时，局部最优值可能会影响算法的表现：在局部最优值处，各个参数的导数都是0。梯度是0（所有导数为0），意味着梯度下降法将不再更新了。

在待优化参数较少时，陷入局部最优值是一种比较常见的情况。而对于参数量巨大的深度学习项目来说，整个模型陷入局部最优值是一个几乎不可能发生的事情。某参数在梯度为0时，既有可能是局部最优值，也可能是局部最差值。不妨设两种情况的概率都是0.5。如果整个模型都陷入了局部最优值，那么所有参数都得处于局部最优值上。假设我们的深度学习模型有10000个参数，则一个梯度为0的点是局部最优值的概率是$0.5^{10000}$，这是一个几乎不可能发生的事件。

所以，在深度学习中，更常见的梯度为0的点是鞍点（某处梯度为0，但不是局部最值）。在鞍点处，有很多参数都处于局部最差值上，只要稍微对这些参数做一些扰动，参数就会往更小的方向移动。因此，鞍点不会对学习算法产生影响。

在深度学习中，一种会影响学习速度的情况叫做“高原”（plateau）。在高原处，梯度的值一直都很小。只有跨过了这段区域，学习的速度才会快起来。这种情况的可视化结果如下：

总而言之，深度学习问题和简单的优化问题不太一样，不用过多担心局部最优值的问题。而高原现象确实会影响学习的速度。

总结

这周，我们围绕深度学习的优化算法，学习了许多提升梯度下降法性能的技术。让我们来捋一捋。

首先，我们可以在处理完一小批数据后就执行梯度下降，而不必等处理完整个数据集后再执行。这种算法叫分批梯度下降（mini-batch gradient descent)。这是一种对梯度下降法的通用改进方法，即默认情况下，这种算法都可以和其他改进方法同时使用。

之后，我们学习了移动平均的概念，知道移动平均值可以更平滑地反映数据在一段时间内的趋势。基于移动平均值，有 gradient descent with momentum 和 RMSProp 这两种梯度下降的改进方法。而现在非常常用的 Adam 优化算法是Momentum 和 RMSProp 的结合版。

最后，我们学习了学习率衰减的一些常见方法。

学完本课的内容后，我认为我们应该对相关知识达到下面的掌握程度：

• 分批梯度下降
  • 了解原理
  • 掌握如何选取合适的 batch size
• 高级优化算法
  • 了解移动平均数的思想
  • 了解 Adam 的公式
  • 记住 Adam 超参数的常见取值
  • 未来学习了编程框架后，会调用 Momentum，Adam 优化器
• 学习率衰减
  • 掌握“学习率衰减能加速收敛”这一概念
  • 在训练自己的模型时，能够有意识地去调小学习率
• 局部最优值
  • 不用管这个问题

代码实战

这周，官方的编程作业还是点集分类。我觉得这个任务太简单了，还是挑战小猫分类比较有意思。

在这周的代码实战项目中，让我们先回顾一下整个项目的框架，再实现这周学到的技术，包括分批梯度下降(Mini-batch Gradient Descent)、高级梯度下降算法(Mini-batch Gradient Descent)、学习率衰减。

项目链接：
​https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/AdvancedOptimizer

小猫分类项目框架

数据集

和之前一样，我们即将使用一个 kaggle 上的猫狗分类数据集。我已经写好了读取数据的函数，该函数的定义如下：

def get_cat_set(
    data_root: str,
    img_shape: Tuple[int, int] = (224, 224),
    train_size=1000,
    test_size=200,
) -> Tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray]:

填入数据集根目录、图像Reszie后的大小、一半训练集的大小、一半测试集的大小，我们就能得到预处理后的train_X, train_Y, dev_X, dev_Y。其中，X的形状是(n_x, m), Y的形状是(1, m)。n_x是图像的特征数，对于一个大小为(224, 224)的图像，n_x = 224*224*3。m是样本数量，如果train_size=1000，则m=2000。

在之前的实战中，我的模型在训练集上的表现都十分糟糕，还没有用到“测试集”的机会。因此，我们之前那个“测试集”，既可以认为是开发集，也可以认为是测试集。从这周开始，出于严谨性的考虑，我准备把之前的“测试集”正式称作开发集（dev set）。

模型类

和之前一样，我们用BaseRegressionModel来表示一个最后一层使用sigmoid，loss用交叉熵的二分类模型基类。这个基类的定义如下：

class BaseRegressionModel(metaclass=abc.ABCMeta):

    def __init__(self):
        pass

    @abc.abstractmethod
    def forward(self, X: np.ndarray, train_mode=True) -> np.ndarray:
        pass

    @abc.abstractmethod
    def backward(self, Y: np.ndarray) -> np.ndarray:
        pass

    @abc.abstractmethod
    def get_grad_dict(self) -> Dict[str, np.ndarray]:
        pass

    @abc.abstractmethod
    def save(self) -> Dict[str, np.ndarray]:
        pass

    @abc.abstractmethod
    def load(self, state_dict: Dict[str, np.ndarray]):
        pass

    def loss(self, Y: np.ndarray, Y_hat: np.ndarray) -> np.ndarray:
        return np.mean(-(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)))

    def evaluate(self, X: np.ndarray, Y: np.ndarray, return_loss=False):
        Y_hat = self.forward(X, train_mode=False)
        Y_hat_predict = np.where(Y_hat > 0.5, 1, 0)
        accuracy = np.mean(np.where(Y_hat_predict == Y, 1, 0))
        if return_loss:
            loss = self.loss(Y, Y_hat)
            return accuracy, loss
        else:
            return accuracy

在模型类中，和训练有关的主要有forward, backward, get_grad_dict这三个方法，分别表示前向传播、反向传播、梯度获取。

这里要对get_grad_dict做一个说明。之前我们都是直接在模型类里实现梯度下降的，但在这周学了新的优化算法后，这种编程方式就不太方便拓展了。因此，从这周开始，我们应该用一个BaseOptimizer类来表示各种梯度下降算法。模型通过get_grad_dict把梯度传给优化器。

除了和训练相关的方法外，模型类通过save, load来把数据存入/取自一个词典，通过loss, evaluate来获取一些模型评测指标。

BaseRegressionModel只是一个抽象基类。实际上，我在本项目使用的是第四周学习的深层神经网络（任意层数的全连接网络）DeepNetwork。只需要传入每一层神经元个数、每一层的激活函数，我们就能得到一个全连接分类网络：

class DeepNetwork(BaseRegressionModel):

    def __init__(self, neuron_cnt: List[int], activation_func: List[str]):
        ...

在第四周代码的基础上，我修改了一下参数初始化的方法。由于隐藏层的激活函数都用的是ReLU，我打算默认使用 He Initialization:

for i in range(self.num_layer):
    self.W.append(
        np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) *
        np.sqrt(2 / neuron_cnt[i]))

除此之外，我没有在这个模型上添加其他高级功能。我也没有添加正则化。现在网络还处于欠拟合状态，等我有资格解决过拟合问题时再去考虑正则化。

优化器类

看完了模型类，接下来，我们来看一看这周要实现的优化器类。所有的优化器类都继承自基类BaseOptimizer。

class BaseOptimizer(metaclass=abc.ABCMeta):

    def __init__(
            self,
            param_dict: Dict[str, np.ndarray],
            learning_rate: float,
            lr_scheduler: Callable[[float, int], float] = const_lr) -> None:
        self.param_dict = param_dict
        self._epoch = 0
        self._num_step = 0
        self._learning_rate_zero = learning_rate
        self._lr_scheduler = lr_scheduler

    @property
    def epoch(self) -> int:
        return self._epoch

    @property
    def learning_rate(self) -> float:
        return self._lr_scheduler(self._learning_rate_zero, self.epoch)

    def increase_epoch(self):
        self._epoch += 1

    def save(self) -> Dict:
        return {'epoch': self._epoch, 'num_step': self._num_step}

    def load(self, state_dict: Dict):
        self._epoch = state_dict['epoch']
        self._num_step = state_dict['num_step']

    def zero_grad(self):
        for k in self.grad_dict:
            self.grad_dict[k] = 0

    def add_grad(self, grad_dict: Dict[str, np.ndarray]):
        for k in self.grad_dict:
            self.grad_dict[k] += grad_dict[k]

    @abc.abstractmethod
    def step(self):
        pass

这个优化器基类实现了以下功能：

• 维护当前的epoch和step，以辅助其他参数的计算。
• 维护当前的学习率，并通过使用_lr_scheduler的方式支持学习率衰减。
• 定义了从词典中保存/读取优化器的方法save, load。
• 定义了维护的梯度的清空梯度方法zero_grad和新增梯度方法add_grad。
• 允许子类实现step方法，以使用不同策略更新参数。

在后续章节中，我会介绍该如何使用这个基类实现这周学过的优化算法。

模型训练

基于上述的BaseRegressionModel和BaseOptimizer，我们可以写出下面的模型训练函数：

def train(model: BaseRegressionModel,
          optimizer: BaseOptimizer,
          X,
          Y,
          total_epoch,
          batch_size,
          model_name: str = 'model',
          save_dir: str = 'work_dirs',
          recover_from: Optional[str] = None,
          print_interval: int = 100,
          dev_X=None,
          dev_Y=None):
    if recover_from:
        load_state_dict(model, optimizer, recover_from)
    
    # Prepare mini_batch
    ...

    for e in range(total_epoch):
        for mini_batch_X, mini_batch_Y in mini_batch_XYs:
            mini_batch_Y_hat = model.forward(mini_batch_X)
            model.backward(mini_batch_Y)
            optimizer.zero_grad()
            optimizer.add_grad(model.get_grad_dict())
            optimizer.step()

        currrent_epoch = optimizer.epoch

        if currrent_epoch % print_interval == 0:
            # print loss
            ...

        optimizer.increase_epoch()

    save_state_dict(model, optimizer,
                    os.path.join(save_dir, f'{model_name}_latest.npz'))

训练之前，我们可以从模型文件recover_from里读取模型状态和优化器状态。读取数据是通过load_state_dict实现的：

def load_state_dict(model: BaseRegressionModel, optimizer: BaseOptimizer,
                    filename: str):
    state_dict = np.load(filename)
    model.load(state_dict['model'])
    optimizer.load(state_dict['optimizer'])

在得到某一批训练数据X, Y后，我们可以用下面的代码执行一步梯度下降：

Y_hat = model.forward(X)
model.backward(Y)
optimizer.zero_grad()
optimizer.add_grad(model.get_grad_dict())
optimizer.step()

我们会先调用模型的前向传播forward和反向传播backward，令模型存下本轮的梯度。之后，我们重置优化器，把梯度从模型传到优化器，再调用优化器进行更新。

训练代码中，默认使用了mini-batch。我会在后续章节介绍mini-batch的具体实现方法。

完成了梯度的更新后，我们要维护当前的训练代数epoch。训练了几代后，我们可以评测模型在整个训练集和开发集上的性能指标。

currrent_epoch = optimizer.epoch

if currrent_epoch % print_interval == 0:
    # print loss
    ...

optimizer.increase_epoch()

最后，模型训练结束后，我们要保存模型。保存模型是通过save_state_dict实现的：

def save_state_dict(model: BaseRegressionModel, optimizer: BaseOptimizer,
                    filename: str):
    state_dict = {'model': model.save(), 'optimizer': optimizer.save()}
    np.savez(filename, **state_dict)

如果你对np.savez函数不熟，欢迎回顾我在第四周代码实战中对其的介绍。

总之，基于我们定义的BaseRegressionModel和BaseOptimizer，我们可以在初始化完这个两个类的对象后，调用train来完成模型的训练。

使用 Mini-batch

注意 I/O 开销！

重申一下，Mini-batch gradient descent 的本意是加快训练速度。如果实现了 Mini-batch 后，程序在其他地方跑得更慢了，那么使用这个算法就毫无意义了。

在我们这个小型的深度学习项目中，从硬盘上读取数据的开销是极大的。下图是执行包含前后处理在内的一轮训练的时间开销分布：

从图中可以看出，相对于一轮训练，读取数据的开销是极大的。读取数据的时间甚至约等于两轮训练的时间。

在之前的项目中，我一直默认是把训练数据全部读取到内存中，然后再进行训练。这样的好处是网络的训练速度不受硬盘读写速度限制，会加快不少，坏处是训练数据的总量受到电脑内存的限制。

在使用分批梯度下降算法时，为了比较算法在性能上的提升，我们应该继续使用相同的数据管理策略，即把数据放到内存中处理。如果换了算法，还换了数据管理策略，把一次性读取数据改成每次需要数据的时候再去读取，那么我们就无法观察到算法对于性能的提升。

事实上，在大型深度学习项目中，模型执行一轮训练的速度很慢，I/O的开销相对来说会小很多。在这种时候，我们可以仅在需要时再读取数据。不过，在这种情况下，我们依然要保证内存/显存足够支持一轮mini-batch的前向/反向传播。这里要注意一下我们这个小demo和实际深度学习项目的区别。

mini-batch 预处理

在执行一个epoch(代)的训练时，我们应该保证训练数据是打乱的，以避免极端数据分布给训练带来的副作用。

epoch 与 epoch 之间 mini-batch 的划分是否相同到不是那么重要。理论上来说，数据越平均越好，最好能每个 epoch 都重新划分 mini-batch。但是，为了加速训练，同时让使用 mini-batch 的逻辑更加易懂，我打算先预处理出 mini-batch，之后每个 epoch 都使用相同的划分。

为了方便之后的处理，我们把每个mini-batch的X和Y都单独存入数组mini_batch_XYs。这样，在之后的训练循环里，每个mini-batch的数据就可以直接拿来用了。以下是预处理mini-batch的代码：

m = X.shape[1]
indices = np.random.permutation(m)
shuffle_X = X[:, indices]
shuffle_Y = Y[:, indices]
num_mini_batch = math.ceil(m / batch_size)
mini_batch_XYs = []
for i in range(num_mini_batch):
    if i == num_mini_batch - 1:
        mini_batch_X = shuffle_X[:, i * batch_size:]
        mini_batch_Y = shuffle_Y[:, i * batch_size:]
    else:
        mini_batch_X = shuffle_X[:, i * batch_size:(i + 1) * batch_size]
        mini_batch_Y = shuffle_Y[:, i * batch_size:(i + 1) * batch_size]
    mini_batch_XYs.append((mini_batch_X, mini_batch_Y))

在这段代码中，我们首先用第二周编程练习中学过的permutation生成一个随机排列，并根据这个随机排列打乱数据。

之后的代码就是一段常见的数据除法分块逻辑。对于除得尽和除不尽的mini-batch，我们分开处理，提取出每个mini_batch的X和Y。

mini-batch 训练

预处理得当的话，用mini-batch进行训练的代码非常简洁。我们只需要在原来的训练循环里加一个对mini-batch的遍历即可：

for e in range(num_epoch):
    for mini_batch_X, mini_batch_Y in mini_batch_XYs:
        mini_batch_Y_hat = model.forward(mini_batch_X)
        model.backward(mini_batch_Y)
        model.gradient_descent(learning_rate)

mini-batch 的损失函数曲线

和我们在课堂里学的一样，使用mini-batch后，损失函数的曲线可能不像之前那么平滑。这是因为我们画损失函数曲线时用的是每个mini-batch上的损失函数，而不是整个训练集的损失函数。我得到的一个mini-batch损失函数曲线如下：

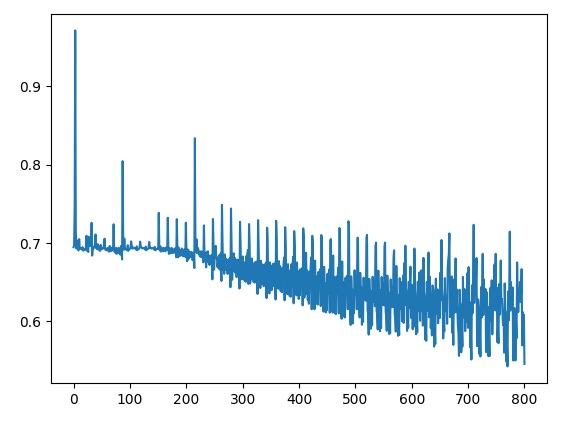
在训练时，我顺手存了一下每个mini-batch的梯度，并在训练结束后对它们进行可视化：

mini_batch_loss_list = []
for e in range(num_epoch):
    for mini_batch_X, mini_batch_Y in mini_batch_XYs:
        ...

        if plot_mini_batch:
            loss = model.loss(mini_batch_Y, mini_batch_Y_hat)
            mini_batch_loss_list.append(loss)
if plot_mini_batch:
    plot_length = len(mini_batch_loss_list)
    plot_x = np.linspace(0, plot_length, plot_length)
    plot_y = np.array(mini_batch_loss_list)
    plt.plot(plot_x, plot_y)
    plt.show()

实现高级优化算法

有了基类BaseOptimizer后，我们只需要实现子类的构造函数和更新函数，就可以实现各种各样的改进梯度下降算法了。让我们看一下这周学习的Momentum, RMSProp, Adam该如何实现。

Momentum

Momentum的主要实现代码如下：

class Momentum(BaseOptimizer):

    def __init__(self,
                 param_dict: Dict[str, np.ndarray],
                 learning_rate: float,
                 beta: float = 0.9,
                 from_scratch=False) -> None:
        super().__init__(param_dict, learning_rate)
        self.beta = beta
        self.grad_dict = deepcopy(self.param_dict)
        if from_scratch:
            self.velocity_dict = deepcopy(self.param_dict)
            for k in self.velocity_dict:
                self.velocity_dict[k] = 0

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.velocity_dict[k] = self.beta * self.velocity_dict[k] + \
                (1 - self.beta) * self.grad_dict[k]
            self.param_dict[k] -= self.learning_rate * self.velocity_dict[k]

在Momentum中，我们主要是维护velocity_dict这个变量。根据课堂里学过的知识，这个变量的值等于梯度的指数移动平均值。因此，我们只需要在step里维护一个指数平均数即可。

为了保存优化器的状态，我们应该在save, load里保存velocity_dict：

def save(self) -> Dict:
    state_dict = super().save()
    state_dict['velocity_dict'] = self.velocity_dict
    return state_dict

def load(self, state_dict: Dict):
    self.velocity_dict = state_dict.get('velocity_dict', None)
    if self.velocity_dict is None:
        self.velocity_dict = deepcopy(self.param_dict)
        for k in self.velocity_dict:
            self.velocity_dict[k] = 0
    super().load(state_dict)

RMSProp

RMSProp的主要实现代码如下：

class RMSProp(BaseOptimizer):

    def __init__(self,
                 param_dict: Dict[str, np.ndarray],
                 learning_rate: float,
                 beta: float = 0.9,
                 eps: float = 1e-6,
                 from_scratch=False,
                 correct_param=True) -> None:
        super().__init__(param_dict, learning_rate)
        self.beta = beta
        self.eps = eps
        self.grad_dict = deepcopy(self.param_dict)
        self.correct_param = correct_param
        if from_scratch:
            self.s_dict = deepcopy(self.param_dict)
            for k in self.s_dict:
                self.s_dict[k] = 0

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.s_dict[k] = self.beta * self.s_dict[k] + \
                (1 - self.beta) * np.square(self.grad_dict[k])
            if self.correct_param:
                s = self.s_dict[k] / (1 - self.beta**self._num_step)
            else:
                s = self.s_dict[k]
            self.param_dict[k] -= self.learning_rate * self.grad_dict[k] / (
                np.sqrt(s + self.eps))

和Momentum类似，我们要维护一个指数平均数权重s_dict，并在更新参数时算上这个权重。由于RMSProp是除法运算，为了防止偶尔出现的除以0现象，我们要在分母里加一个极小值eps。

我在这个优化器中加入了偏差校准功能。如果开启了校准，指数平均数会除以一个(1 - self.beta**self._num_step)。

类似地，RMSProp中也用save, load来保存状态s_dict。

def save(self) -> Dict:
    state_dict = super().save()
    state_dict['s_dict'] = self.s_dict
    return state_dict

def load(self, state_dict: Dict):
    self.s_dict = state_dict.get('s_dict', None)
    if self.s_dict is None:
        self.s_dict = deepcopy(self.param_dict)
        for k in self.s_dict:
            self.s_dict[k] = 0
    super().load(state_dict)

注意，RMSProp实际上是对学习率进行了一个放缩。在把模型的优化算法从Momentum改成RMSProp后，学习率要从头调整。一般来说，RMSProp里的权重s_dict是一个小于1的数。这个数做了分母，等价于放大了学习率。因此，使用RMSProp后，可以先尝试把学习率调小100倍左右，再做进一步的调整。

Adam

Adam 的主要实现代码如下：

class Adam(BaseOptimizer):

    def __init__(self,
                 param_dict: Dict[str, np.ndarray],
                 learning_rate: float,
                 beta1: float = 0.9,
                 beta2: float = 0.999,
                 eps: float = 1e-8,
                 from_scratch=False,
                 correct_param=True) -> None:
        super().__init__(param_dict, learning_rate)
        self.beta1 = beta1
        self.beta2 = beta2
        self.eps = eps
        self.grad_dict = deepcopy(self.param_dict)
        self.correct_param = correct_param
        if from_scratch:
            self.v_dict = deepcopy(self.param_dict)
            self.s_dict = deepcopy(self.param_dict)
            for k in self.v_dict:
                self.v_dict[k] = 0
                self.s_dict[k] = 0

    def step(self):
        self._num_step += 1
        for k in self.param_dict:
            self.v_dict[k] = self.beta1 * self.v_dict[k] + \
                (1 - self.beta1) * self.grad_dict[k]
            self.s_dict[k] = self.beta2 * self.s_dict[k] + \
                (1 - self.beta2) * (self.grad_dict[k] ** 2)
            if self.correct_param:
                v = self.v_dict[k] / (1 - self.beta1**self._num_step)
                s = self.s_dict[k] / (1 - self.beta2**self._num_step)
            else:
                v = self.v_dict[k]
                s = self.s_dict[k]
            self.param_dict[k] -= self.learning_rate * v / (np.sqrt(s) +
                                                            self.eps)

Adam 就是把 Momentum 和 RMSProp 结合一下。在Adam中，我们维护v_dict和s_dict两个变量，并根据公式利用这两个变量更新参数。

这里有一个小细节：在Adam中，eps是写在根号外的，而RMSProp中eps是在根号里面的。这是为了与原论文统一。其实eps写哪都差不多，只要不让分母为0即可。

类似地，Adam要在状态词典里保存两个变量：

def save(self) -> Dict:
    state_dict = super().save()
    state_dict['v_dict'] = self.v_dict
    state_dict['s_dict'] = self.s_dict
    return state_dict

def load(self, state_dict: Dict):
    self.v_dict = state_dict.get('v_dict', None)
    self.s_dict = state_dict.get('s_dict', None)
    if self.v_dict is None:
        self.v_dict = deepcopy(self.param_dict)
        for k in self.v_dict:
            self.v_dict[k] = 0
    if self.s_dict is None:
        self.s_dict = deepcopy(self.param_dict)
        for k in self.s_dict:
            self.s_dict[k] = 0
    super().load(state_dict)

Adam使用的学习率和RMSProp差不多。如果有一个在RMSProp上调好的学习率，可以直接从那个学习率开始调。

学习率衰减

要实现学习率衰减非常容易，我们只需要用一个实时计算学习率的学习率getter来代替静态的学习率即可。在BaseOptimizer中，我们可以这样实现学习率衰减：

class BaseOptimizer(metaclass=abc.ABCMeta):

    def __init__(
            self,
            param_dict: Dict[str, np.ndarray],
            learning_rate: float,
            lr_scheduler: Callable[[float, int], float] = const_lr) -> None:
        self.param_dict = param_dict
        self._epoch = 0
        self._num_step = 0
        self._learning_rate_zero = learning_rate
        self._lr_scheduler = lr_scheduler

    @property
    def learning_rate(self) -> float:
        return self._lr_scheduler(self._learning_rate_zero, self.epoch)

在BaseOptimizer类中，我们用@property装饰器装饰一个learning_rate方法，以实现一个getter函数。这样，我们在获取optimizer.learning_rate这个属性时，实际上是在调用learning_rate这个函数。

在getter中，我们用_lr_scheduler来实时计算一个学习率。_lr_scheduler是一个函数，该函数应该接受初始学习率、当前的epoch这两个变量，返回一个当前学习率。通过修改这个_lr_scheduler，我们就能使用不同的学习率衰减算法。

在代码中，我只实现了两个简单的学习率衰减函数。首先是常数学习率：

def const_lr(learning_rate_zero: float, epoch: int) -> float:
    return learning_rate_zero

之后是课堂上学过的双曲线衰减函数：

def get_hyperbola_func(decay_rate: float) -> Callable[[float, int], float]:

    def scheduler(learning_rate_zero: float, epoch: int):
        return learning_rate_zero / (1 + epoch * decay_rate)

    return scheduler

get_hyperbola_func是一个返回函数的函数。我们可以用get_hyperbola_func(decay_rate)生成一个某衰减率的学习率衰减函数。

实验结果

经实验，高级优化技术确实令训练速度有显著的提升。为了比较不同优化技术的性能，我使用2000个小猫分类样本作为训练集，使用了下图所示的全连接网络，比较了不同batch size、不同优化算法、不同学习率衰减方法下整个数据集的损失函数变化趋势。

以下是实验的结果：

首先，我比较了不同batch size下的mini-batch梯度下降。

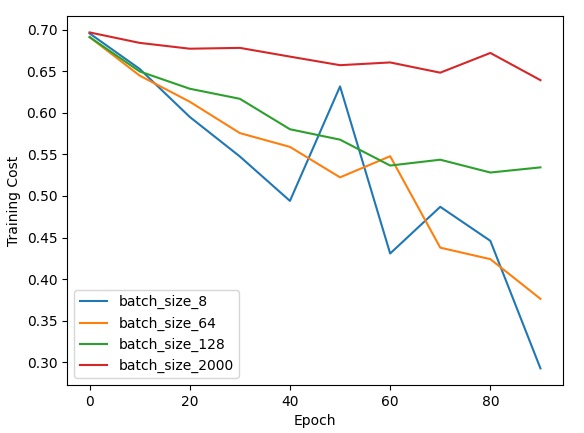
从理论上来看，对于同一个数据集，执行相同的epoch，batch size越小，执行优化的次数越多，优化的效果越好。但是，batch size越小，执行一个epoch花的时间就越多。batch size过小的话，计算单元的向量化计算无法得到充分利用，算法的优化效率（单位时间内的优化量）反而下降了。

上面的实验结果和理论一致。执行相同的epoch，batch size越小，优化的效果越好。同时，batch size越小，误差也更容易出现震荡。虽然看上去batch size越小效果就越好，但由于向量化计算的原因，batch size为64,128,2000时跑一个epoch都差不多快，batch size为8时跑一个epoch就很慢了。我还尝试了batch size为1的随机梯度下降，算法跑一个epoch的速度奇慢无比，程序运行效率极低。最终，我把64作为所有优化算法的batch size。

之后，我比较了普通梯度下降、Momentum、RMSProp、Adam的优化结果。在普通梯度下降和Momentum中，我的学习率为1e-3；在RMSProp和Adam中，我的学习率为1e-5。

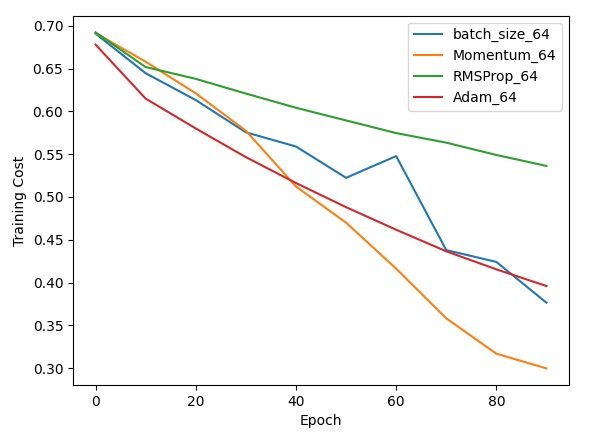
由于不同算法的学习率“尺度”不一样，因此，应该去比较普通梯度下降和Momentum，RMSProp和Adam这两组学习率尺度一样的实验。

对比普通梯度下降和Momentum，可以看出Momentum能够显著地提升梯度下降的性能，并且让误差的变化更加平滑。

对比RMSProp和Adam，可以看出学习率相同且偏小的情况下，Adam优于RMSProp。

感觉Adam的性能还是最优秀的。如果把Adam的学习率再调一调，优化效果应该能够超过其他算法。

最后，我还尝试了三个学习率衰减策略实验。每次实验都使用Adam优化器，初始学习率都是1e-5。第一次实验固定学习率，之后的两次实验分别使用衰减系数0.2，0.005的双曲线衰减公式。以下是实验结果：

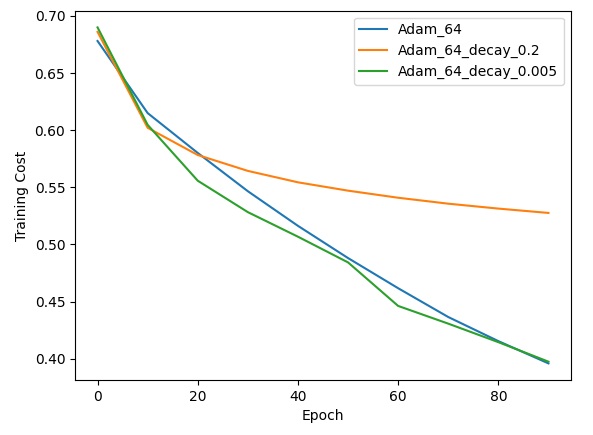
从图中可以看出，由于初始学习率较低，在使用了比较大的衰减系数（=0.2）时，虽然学习的过程很平滑，但是学习速度较慢。而如果使用了恰当的衰减系数，虽然学习率在缓缓降低，但学习的步伐可能更加恰当，学习的速度反而变快了。

不过，RMSProp本身就自带调度学习率的效果。主动使用学习率衰减的效果可能没有那么明显。相比mini-batch和高级优化算法，学习率衰减确实只能算是一种可选的策略。

感想

我的实验还做得不是很充分。理论上可以再调一调学习率，更加公平地比较不同的学习算法。但是，我已经没有动力去进一步优化超参数了——由于目前学习算法的性能过于优秀，模型已经在训练集上过拟合了，训练准确率达到了80%多，远大于58%的开发准确率。因此，根据上一周学的知识，我的下一步任务不是继续降低训练误差，而是应该使用正则化方法或者其他手段，提高模型的泛化能力。在后续的课程中，我们还会接着学习改进深度学习项目的方法，届时我将继续改进这个小猫分类模型。

其实，过拟合对我来说是一件可喜可贺的事情。前两周，仅使用普通梯度下降时，模型的训练准确率和测试准确率都很低，我还在怀疑是不是我的代码写错了。现在看来，这完全是梯度下降算法的锅。朴素的梯度下降算法的性能实在是太差了。稍微使用了mini-batch、高级优化算法等技术后，模型的训练速度就能有一个质的飞跃。在深度学习项目中，mini-batch, Adam优化器应该成为优化算法的默认配置。