吴恩达《深度学习专项》笔记（十三）：CNN应用：人脸识别与风格迁移

在这堂课里，我们要学习两个具体的应用：人脸识别、风格迁移。

相信大家已经在很多地方见识过人脸识别应用了：在火车站，要通过身份证和人脸核实身份；办理业务时，可以用手机完成人脸识别以核实身份；进办公楼时，员工只要刷脸通过就可以打开门禁。通过这节课的学习，我们能够学会如何用CNN完成人脸识别。

神经网络风格迁移是一项有趣的应用。它利用了CNN捕捉图像抽象信息的特点，能够把一幅图像的风格转移到另一幅图像上，从而生成一幅新的图像。这项技术不需要从头训练网络，学完这门课后，我们能快速地用代码实现神经网络风格迁移。

课堂笔记

人脸识别

准确来说，在人脸识别(Face Recognition)任务中，会给定一个有$K$个人的数据库。之后，每一次识别都会输入一张图片，输出这张图片是$K$个人中的哪一个，或者没有检测到相关人士。

有一个与这个相关的任务叫做人脸验证(Face Verification)。这个任务稍微简单一些，输入是一张图片和一个标记身份的数据（比如身份证号），要求输出图片中的人是否符合该身份。

单样本学习

按我们之前学的方法，假如我们在$K$个人的数据库上做识别（分类）任务，应该套用一个CNN模型，并在模型最后接一个$K+1$类的softmax，表示输入图片是K个人中的哪一个，或者都不是。

但是，这样的架构不适合人脸识别任务。以公司的门禁识别为例，这种方法有如下的缺点：

1. 每来一个新同事，模型就要重新训练一次。
2. 每个人都得上传大量的个人照片供网络训练。

理想情况下，我们希望模型能从一张人脸照片中学会分辨这张人脸，这样每个新同事只需要上传一张照片即可。这叫做单样本学习(One-shot Learning)。

为了完成单样本学习，我们可以从另一个角度来建模人脸识别问题：如果输入的人脸和数据库里某张人脸极为相似，我们就说识别出了这张人脸；否则，就说没有识别到有效的人脸。

这样，人脸识别问题就被转换为了一个求两张图片相似度的问题。我们可以让网络学习一个输入是两张图片，输出是二者相似度的一个映射。

孪生网络

在完成和相似度有关的问题时，一种常见的做法是使用孪生网络（Siamese Network)。

假设网络的倒数第二层有128个神经元。在普通分类网络中，这128个神经元输出的长度为128的向量会被输入进最后的softmax层。而在孪生网络中，我们要去掉softmax层，并用这个没有sofrmax的网络$f$分别输出两张图片$x^{(1)}, x^{(2)}$对应的128维向量$f(x^{(1)}), f(x^{(2)})$。这样，每张图片有了唯一对应的一个128维向量，这个向量可以看成是该图片的编码(encoding)。而我们又知道，对向量求相似度是很方便的。我们可以利用两张图片的编码求出相似度。

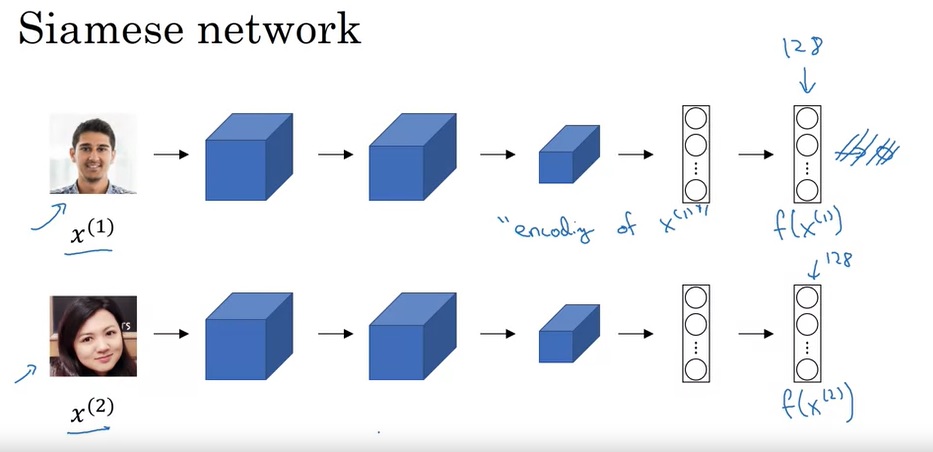
说起向量的相似度，最容易想到是向量间的距离$||v - u||^2$。因此，我们可以i设法让网络学会这样一种关系：

• 若$x^{(i)}, x^{(j)}$是同一人，则$||f(x^{(i)}) - f(x^{(j)})||^2$很小。
• 若$x^{(i)}, x^{(j)}$不是同一人，则$||f(x^{(i)}) - f(x^{(j)})||^2$很大。、

为了达成这个目标，我们来看看应该用怎样的误差来指导网络的优化方向。

三元组误差

在让网络学习基于距离的相似度时，一种常用的误差是三元组误差(Triplet Loss)。

在一轮训练中，我们要用到3张图片：一张基准图(anchor)$A$和与其相对的正负样本$P, N$各一张。设$d(A, B)$为图片$A, B$的编码的距离，则我们希望$d(A, P) \leq d(A, N)$。

左边的人是吴恩达的妻子，这几张图片已经出现了好几次。

移个项，即我们希望：

$$d(A, P) - d(A, N) \leq 0.$$

但这个条件太容易满足了，令$f(x)=0$恒成立的话无论怎样的输入都可以使上式左侧为0了。因此，我们要加一点小小的约束：

$$d(A, P) - d(A, N) + \alpha \leq 0,$$

这个$\alpha$是一个较小的数，比如可以令$\alpha=0.2$。为了达成这个目标，我们可以设置以下的误差函数

$$L(A, P, N)=max(d(A, P) - d(A, N) + \alpha, 0).$$

这里取max的直观解释是：只要满足开始那个不等式，让正样本和负样本能够分清楚就行了。至于两类样本要不要分辨得那么分明，我们并不关心。

为了利用这个误差训练网络，我们要在训练集里为同一个人准备多张照片。比如1000个人，每人100张照片，共100000张照片构成训练集。

在提出此设计的FaceNet中，还有一些小细节：为了加大训练难度，让模型效果更好，每次训练时应该选择较难的三元组$A, P, N$。详情请阅读原论文。

人脸验证与二分类问题

其实，判断两张图片的编码是否相似的问题可以简单地转化成一个二分类问题：把两张图片的编码“拼起来”，输入进一个逻辑回归的单元，让网络输入两张图片是否相似。

这里把两张图片“拼起来”有很多的实现方式。一种简单的方式是求两个编码的绝对值（L1距离）。

另外，在部署时，由于比较的图像的编码是可以预处理的，只需要用神经网络跑一遍输入图片即可。

神经网络风格迁移

我之前写了一篇详细介绍神经网络风格迁移的文章，我认为那篇文章比这堂课更好理解，非常推荐大家阅读。因此，这部分笔记我会写得潦草一些。

什么是神经网络风格迁移？

如上图所示，在神经网络风格迁移中，输入一张表示内容的图(C)和一张表示画家风格的图(S)，我们可以借助神经网络生成一幅融合内容与风格的图片(G)。

接下来实现神经网络风格迁移时，我们会关注CNN浅层和深层提取出来的特征。因此，在具体介绍风格迁移的实现之前，我们先来看看CNN各层网络究竟学到了什么。

深度卷积网络学到了什么？

为了设法可视化神经网络每一层的输出，我们可以考虑把整个训练集喂入网络，找出使某一层某一神经元激活输出最大的几个像素块。

以AlexNet为例，令第一层某几个神经元激活输出最大的像素块是：

可以看出，浅层的神经网络更关注不同方向轮廓信息。

用同样的方式可视化更深的层，可以看出网络关注的信息越来越抽象。

损失函数

和优化一个网络的参数不同，在神经网络风格迁移中，我们要把一幅图像当成可以优化的参数，通过修改图像的像素值来最小化一个损失函数。让我们看看这个损失函数是怎么定义的。

损失函数由两部分构成：生成图像(G)和内容图像(C)的内容损失与和风格图像(S)的风格损失。二者之间的比例靠比例系数$\alpha, \beta$控制。

$$J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S, G).$$

我们来看一个优化这个损失函数的步骤示例：

1. 生成一个随机图像$G: 100 \times 100 \times 3$
2. 使用梯度下降更新$G$，最小化$J(G)$

内容损失

内容损失的计算方式如下：

1. 使用一个预训练的网络（最常用的是VGG）。
2. 选择神经网络中的某一层$l$，这一层相关的数据会用来计算内容损失。$l$越浅，表示越具体的图像；$l$越深，表示越抽象的图像。一般选取适中的$l$。
3. 令$a^{l}, a^{[l][G]}$为图像$C, G$网络第$l$层的激活输出。我们认为，如果这两个值很相似，则两幅图像的内容就很相似。
4. 令$J_{content}(C, G) = ||a^{l} - a^{[l][G]}||^2$

风格损失

看完了内容损失，现在来看风格损失的计算方式。我们刚刚一直在用名词“风格”。这个词放在美术里，可以指画家的绘画风格。而对于神经网络来说，“风格”又是什么意思呢？

和刚刚的内容损失类似，计算风格损失时，我们也要选择CNN的某层$l$，计算这一层卷积激活输出的通道相关量。

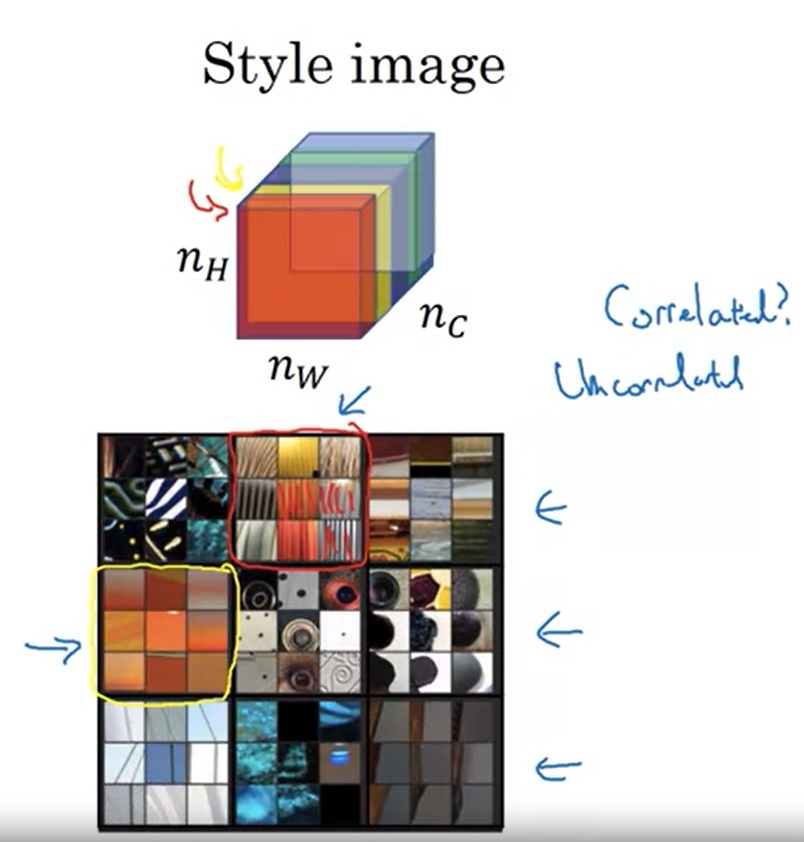
这里“通道相关量”反映的是图像各个通道间两两的相关关系。这句话可能有点拗口，让我们看一个详细的通道相关量示例。

假设一个激活输出有5个通道，我们用颜色“红-黄-紫-绿-蓝”称呼它们。每个通道表示的是一类特征，比如红色的通道表示图像有没有竖着的条纹，黄色通道表示图像有没有橙色的色块。我们想计算红黄通道之间的相关量，其实就是计算图像每个像素处红色通道的值和绿色通道的值之间的相关关系，看看它们是会同时出现，还是一个出现了另一个就不出现。（两个数值的相关量就是它们的乘积，具体的数学表示会在后文中给出）

为什么这样的相关关系能够捕捉到风格信息呢？红色通道和黄色通道的相关关系，就是是不是有竖条纹的地方就有橙色色块。这样一种线条和颜色的关联，就可以代表图片的风格。（下图中红色的框和黄色的框分别圈出了两种特征）

从直觉上认识了风格，现在我们来看一看风格的具体计算方法。在计算两个向量的相关量时，可以直接求两个向量的积。因此，我们要用到一种叫做”风格矩阵“的中间量，它计算了所有通道向量的乘积：

$$G^{[l]}_{kk'}=\Sigma_i^{H} \Sigma_i^{W} a^{[l]}_{i, j, k} a^{[l]}_{i, j, k'}$$

其中，$a^{[l]}_{i, j, k}$是第$i$行$j$列第$k$个通道的激活输出，风格矩阵$G$的形状是$n_c^{[l]} \times n_c^{[l]}$，$G^{[l]}_{kk’}$描述的是第$l$层激活输出中，第$k, k’$个通道间的相关量。

在数学中这个矩阵叫做gram矩阵。

有了风格矩阵，就可以算风格损失了。为了简化表示，我们用$G^{[l]}(S), G^{[l]}(G)$分别表示风格图像S和生成图像G的风格矩阵。和刚刚一样，我们选择一层$l$，并计算风格误差：

$$J^{[l]}_{style}(S, G) = ||G^{[l]}(S)- G^{[l]}(G)||_F^2$$

这是一层上的风格误差。其实，我们还可以指定多个层上的风格误差，以使生成图像能够拟合风格图像在多个卷积层上（抽象程度不同）的风格。多个层的风格误差就是各层风格误差之和。

1D和3D上的卷积

在结束这门课之前，我们来学习最后一项内容——1D和3D数据上的卷积。之前，我们只关注2D的图像数据，当维度不是2时，卷积有怎样的变化呢？

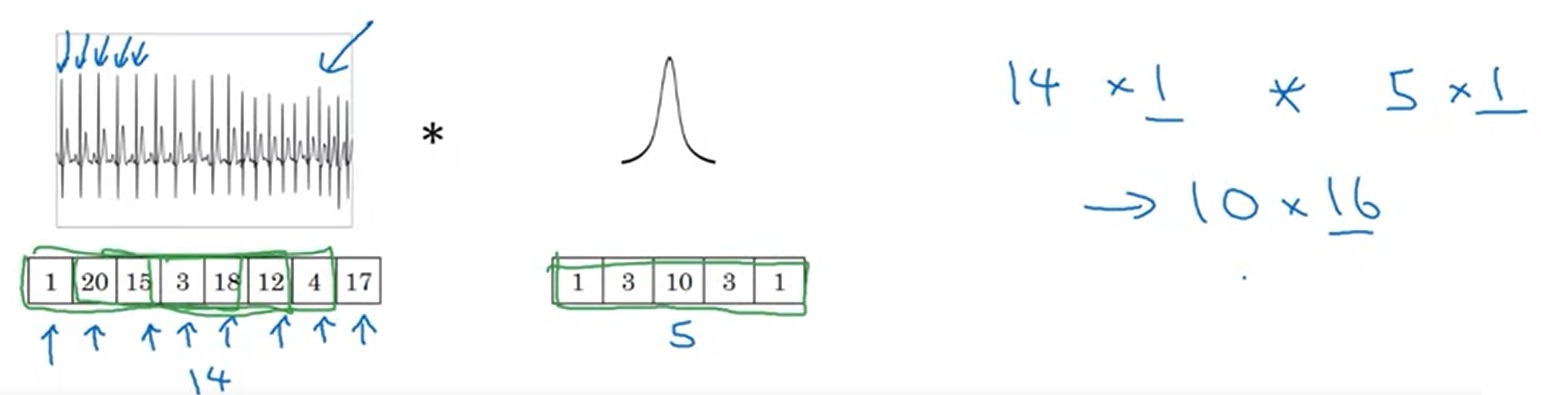
1D数据可以是心电图。和可以用2D卷积捕捉2D图像的边缘一样，我们可以用下图中那个尖尖的1D卷积来捕获高频的数据。1D卷积前后的形状变化规律和2D一样，比如用16个长度为5的卷积卷一个$14 \times 1$的1D图像，可以得到$10 \times 16$的1D图像（第一维是图像长度，第二维是通道数）。

3D数据也是类似的道理。用16个$5 \times 5 \times 5$的卷积核卷一个单通道$14 \times 14 \times 14$的单通道图像，可以得到一个$5 \times 5 \times 5 \times 16$的图像。

总结

这节课主要介绍了人脸识别和神经网络风格迁移两项任务，最后顺便介绍了1D和3D上的卷积。

• 人脸识别
  • 人脸验证与人脸识别任务的定义
  • 如何对单样本学习建模
  • 孪生网络
  • 基于三元组误差和二分类误差的人脸识别网络
• 神经网络风格迁移
  • 神经网络风格迁移的输入输出
  • 利用小技巧可视化 CNN 学到的图像信息
  • 生成风格迁移图像时的内容误差与风格误差

人脸识别任务依赖于数据集，项目搭建起来比较麻烦。对于这一周的内容，我就不展示其他的代码实战笔记了，欢迎阅读我之前写的神经网络风格迁移的实现。