吴恩达《深度学习专项》笔记（十四）：循环神经网络基础

在上一门课中，我们学习了如何用CNN处理网格状的数据。由于最常见的网格状数据是图像，我们主要学习了如何用CNN完成和图像相关的任务。而在这一门课中，我们要学习如何用循环神经网络（RNN）等序列模型处理序列数据。序列数据的种类就比较丰富多彩了：

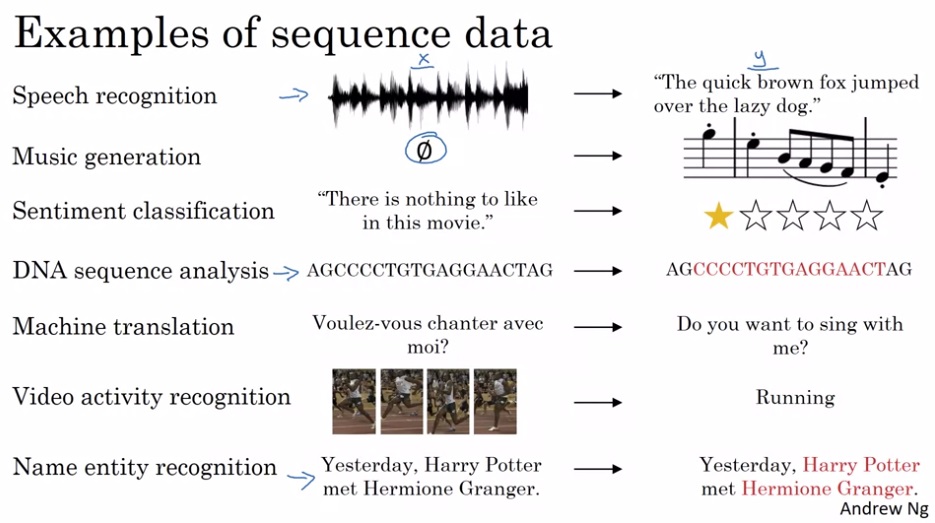
如上图所示，对于语音识别、音乐生成、情绪分类、DNA序列分析、机器翻译、视频动作识别、命名实体识别这些任务，它们的输入和输出至少有一个是某类序列数据，它们都可以用序列模型来建模。

计算机科学中的自然语言处理（NLP）任务常常需要使用序列模型。我们在学这门课时，主要会围绕NLP问题进行讨论。

符号标记

序列数据需要用到一些新的符号标记。在开始正式学习之前，我们先以命名实体识别任务为例，认识一下这些新的符号标记。

命名实体识别任务要求找出句子中的有意义的人名、地名等特殊名词。以这个任务的一个训练样本为例，我们来看一看序列数据的符号标记。

设输入是 Harry Potter and Hermione Granger invented a new spell。

命名实体识别任务的输出$y$也是一个序列。序列的每一个元素是1或0，表示输入中对应的单词是否为命名实体。刚刚那个输入对应的输出应该是1 1 0 1 1 0 0 0 0。

输入输出都由单词或数字组成的序列。设输入为$x$，序列中的第$i$个单词记作$x^{< i >}$。比如$x^{< 2 >}$ = Potter。整个序列的长度$T_x=9$。同理，输出序列中的第$i$个元素记作$y^{< i >}$，整个序列的长度$T_y=9$。

对于第$i$个样本而言，其输入的长度为$T_x^{(i)}$，第$t$个单词为$x^{(i)< t >}$。值得注意的是，每个样本的长度可能不一致。

在表示这些数据时，还有一个问题：怎么表示一个单词？计算机可不认识一大堆字母。为了让只懂数字的计算机能够分清不同的单词，我们要先准备一个词汇表，并用单词在词汇表里的one-hot编码作为单词的表示。比如Harry是长度为10000的词汇表里第4075个单词，则Harry的表示是$[0, 0, 0…,0, 1, 0, …, 0]$，这个向量的长度是10000，只有第4075个元素是1，其他地方都是0。

在大型的模型中，词汇表的大小会是30000至50000，甚至有100000的。

有了这些符号标记，和序列数据有关的任务就可以完全用数学语言表示了。比如对于命名实体识别任务，每一条样本输入是一个向量序列，输出是一个01的数字序列。

循环神经网络模型

在序列问题上使用标准神经网络（全连接网络）会有几个问题：

• 每个样本的长度可能不一致。尽管我们可以找到一个最大的长度，并对长度不足的样本进行零填充，但这种做法看上去就不太好。
• 同一个单词在不同的位置时应该算出类似的特征。而标准神经网络会把每个位置的输入区别对待，无法共享各个位置的知识。
• 和图像数据类似，序列数据的输入长度也很大。假如一个句子有10个单词，词汇表的大小是10000，则输入向量的大小就是100000。这样，神经网络第一层的参数量会很大，网络会过拟合。

因此，我们要用一些其他的架构来处理序列数据以规避这些问题。其中一种可行的架构就是循环神经网络(Recurrent Neural Network, RNN)。

RNN运算过程如下图所示。在RNN中，对于一个样本，我们每次只输入一个单词$x^{< t >}$，得到一个输出$y^{< t >}$。除了输出$y^{< t >}$外，神经网络还会把中间激活输出$a^{< t >}$传递给下一轮计算，这个$a^{< t >}$记录了之前单词的某些信息。所有的输出按照这种方法依次计算。当然，第一轮计算时也会用到激活输出$a^{< 0 >}$，简单地令$a^{< 0 >}$为零张量即可。注意，所有的计算都是用同一个权重一样的神经网络。

有些文章会把一行RNN计算折叠成一个带循环箭头的神经网络，这只是另一种画图的方法：

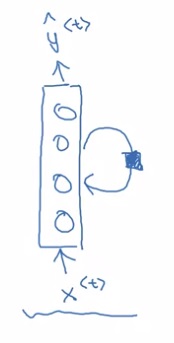
看完了示意图，让我们看看怎样用数学语言表示RNN。在第$t$轮计算中：

$$\begin{aligned} a^{< t >} &= g_1(W_{ax} x^{< t >} + W_{aa} a^{< t - 1 >} + b_a) \\ \hat{y}^{< t >} &=g_2(W_{ya} a^{< t >} + b_y) \end{aligned}$$

其中，$W_{ij}$表示用于计算$i$的，乘在$j$上的矩阵。$g$是激活函数。中间层激活函数多数情况下用tanh，也可以用ReLU。输出的激活函数视任务而定，在二分类的命名实体识别中，输出激活函数是sigmoid。

为了简化表示，可以把$W_{ax}, W_{aa}$拼一下，$x^{< t >}, a^{< t - 1 >}$拼一下：

$$\begin{aligned} W_a &= [W_{aa} | W_{ax}] \\ [a^{< t - 1 >}, x^{< t >}] &= \left[ \begin{matrix} a^{< t - 1 >} \\ --- \\ x^{< t >} \end{matrix} \right] \end{aligned}$$

这样，原来的式子就可以化简了：

$$\begin{aligned} a^{< t >} &= g_1(W_{a} [a^{< t - 1 >}, x^{< t >}] + b_a) \\ \hat{y}^{< t >} &=g_2(W_{y} a^{< t >} + b_y) \end{aligned}$$

RNN也有一些问题。首先，显而易见，每个RNN的输出只能看到它之前的单词。这样是不太好的。比如一句话第一个单词是Teddy，你不知道这是一个人名，还是Teddy bear这样一个普通的物体。稍后我们会学习双向的RNN以解决此问题。

另外，RNN也会面临标准神经网络的梯度爆炸问题。后几节会介绍一些更高级的RNN架构。

「穿越时空之反向传播」

看完了正向传播，我们稍微看一下RNN反向传播的过程。

反向传播前，先要定义一个误差函数。对于命名实体识别这种结果是01的问题，可以继续采用交叉熵误差，即对于序列中每一个元素：

$$L^{< t >}(y^{< t >}, \hat{y}^{< t >}) = -(y^{< t >}log\hat{y}^{< t >}+(1 - y^{< t >})log(1 - \hat{y}^{< t >}))$$

对于一个样本：

$$L(y, \hat{y}) = -\Sigma_{t=1}^{T_y}(y^{< t >}log\hat{y}^{< t >}+(1 - y^{< t >})log(1 - \hat{y}^{< t >}))$$

接下来是反向传播的过程。RNN的计算虽然复杂了一些，但它本质上还是一个计算图。如下图所示，按照红色箭头的方向对变量反向求导即可：

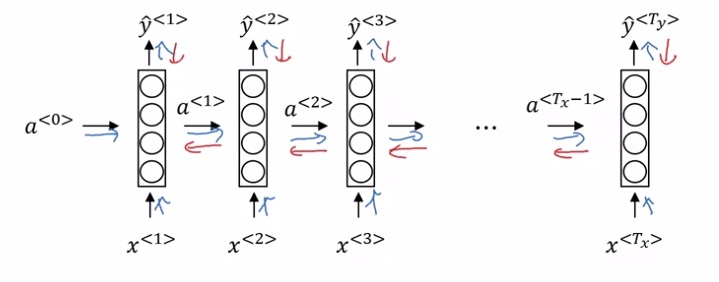
使用了编程框架后，反向传播可以自动由框架完成，可以不需要关心里面的细节了。

由于序列数据有先后的概念，而RNN的反向传播又是从后面的数据向前面的数据进行，因此这样的反向传播有着「穿越时空之反向传播」的称呼。

不同输入输出格式的RNN

刚刚学习的那种RNN只能描述输入输出长度一致的任务。在那种架构的基础上稍作修改，我们就能得到描述各种输入输出格式的任务。

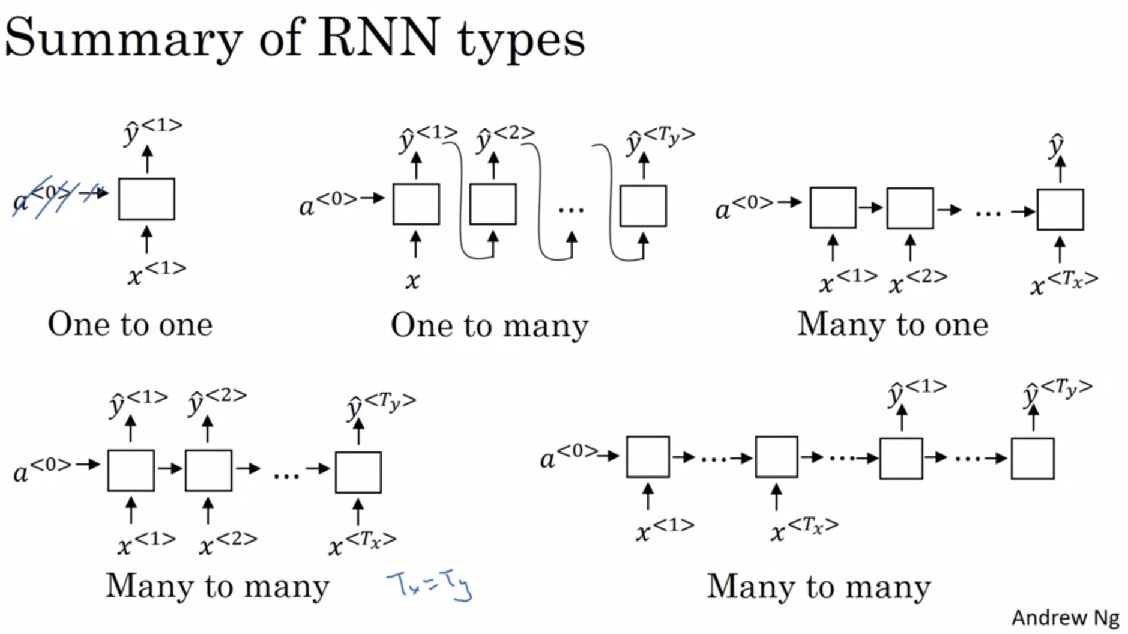
• 一对一：其实一对一问题就是标准神经网络，可以不要那个激活输入$a$。
• 一对多：只把输入放入第一轮计算中，后续计算的输入是上一轮的输出。
• 多对一：只输出最后一轮计算的结果。
• 等长多对多：输入一个元素就输出一个元素。
• 不等长多对多：先做几轮不产生输出的计算（编码器），再做几轮只产生输出的计算（解码器）。解码器的输入也可以和一对多一样，来自于上一轮的输出（图中没有画出）。

RNN应用：语言模型

为了加深对RNN的理解，我们来看一个基于RNN的应用——语言模型。

语言模型是NLP中的一个基础任务。一个语言模型能够输出某种语言某句话的出现概率。通过比较不同句子的出现概率，我们能够开发出很多应用。比如在英语里，同音的”apple and pear”比”apple and pair”的出现概率高（更可能是一个合理的句子）。当一个语音识别软件听到这句话时，可以分别写下这两句发音相近的句子，再根据语言模型断定这句话应该写成前者。

也就是说，对于一句话$x^{< 1 >}…x^{< T_x >}$，语言模型的输出是$P(x^{< 1 >},…, x^{< T_x >})$。这个式子也可以写成$P(x^{< 1 >}) \times P(x^{< 2 >} |x^{< 1 >}) \times P(x^{< 3 >} |x^{< 1 >}, x^{< 2 >}) … \times P(x^{< T_x >} |x^{< 1 >}, x^{< 2 >}, …, x^{< T_x-1 >})$，即一句话的出现概率，等于第一个单词出现在句首的概率，乘上第二个单词在第一个单词之后的概率，乘上第三个单词再第一、二个单词之后的概率，这样一直乘下去。

在训练语言模型时，我们一般要用到语料库(corpus)。语料库包含了某种语言大量的通顺的句子。我们希望一个模型能够学习到这些句子中的规律，知道一句话在这种语言中的出现概率是多少。

语言模型可以用RNN巧妙地实现。整个实现分两步：数据预处理和模型训练。

由于语料库中包含的是自然语言，而RNN的输入是one-hot编码，所以这中间要经过一个预处理的步骤。在NLP中，这一步骤叫做符号化(tokenize)。如我们在「符号标记」一节所学的，我们可以找来一个大小为10000的词汇表，根据每个单词在词汇表中的位置，生成一个one-hot编码。除了普通的词汇外，NLP中还有一些特殊的符号，比如表示句尾的<EOS> (End Of Sentence)，表示词汇表里没有的词的<UNK> (Unknown)。

经过预处理后，语料库里的每一句自然语言就变成了训练样本$x^{< 1 >} … x^{< T_x >}$。我们可以把每一句话输入RNN，巧妙地训练一个语言模型：

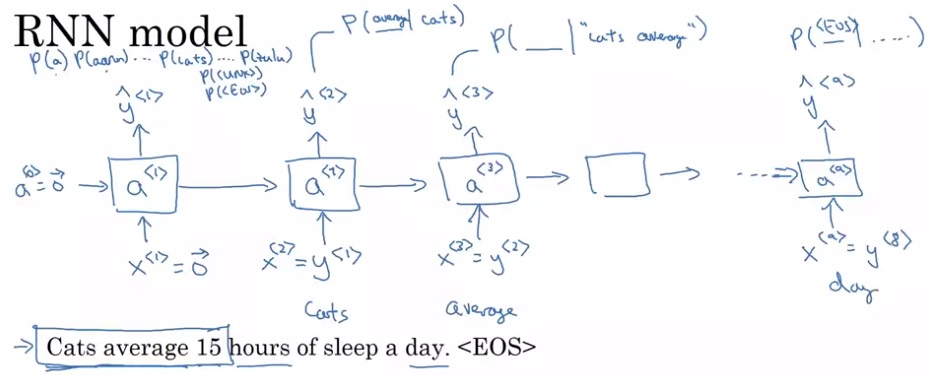
这个计算过程初次接触时有些令人费解，我们慢慢来看懂它。先竖着看一轮计算是怎么完成的。对于每一轮计算，都会给定一个单词编码$x^{< i >}$，输出一个softmax后的概率分布$\hat{y}^{< i >}$，它要对齐的训练标签是训练集某一句话的某个单词$y^{< i >}$。$\hat{y}$表示接收之前所有的输入单词后，此时刻应该输出某单词的概率分布，这个输出的含义和多分类中的类似。

算出这样的$\hat{y}$有什么用呢？别急，再横着看一遍。回忆一下，语言模型要求的概率可以写成$P(y^{< 1 >}) \times P(y^{< 2 >} |y^{< 1 >}) \times P(y^{< 3 >} |y^{< 1 >}, y^{< 2 >}) …$。RNN每一轮的输出，其实就是要拟合$P(y^{< 1 >})$, $P(y^{< 2 >} |y^{< 1 >})$, $P(y^{< 3 >} |y^{< 1 >}, y^{< 2 >})$, …。每一个条件概率的条件，就是每一轮RNN的输入；每一个条件概率的待求事件，就是每一轮RNN的训练标签。比如$P(y^{< 3 >} |y^{< 1 >}, y^{< 2 >})$这个条件概率，它的条件是$y^{< 1 >}, y^{< 2 >}$，待求事件是$y^{< 3 >}$，所以第三轮RNN的标签是$y^{< 3 >}$，输入是$y^{< 1 >}, y^{< 2 >}$（别忘了，在RNN中，前几轮的输入其实也影响了后续的计算）。当然，第一个概率$P(y^{< 1 >})$没有条件，所以第一轮的输入$x^{< 1 >}=0$。对softmax的结果依然使用的是交叉熵误差，一个序列的误差等于所有元素的误差之和。

刚刚介绍的是训练过程。在用这个模型计算某句子的概率时，只要把一个句子输入进这个RNN，再去softmax的概率分布里取出需要的概率，一乘，就能算出语言模型要求的整句话的概率了。比如Cats average 15 hours of sleep a day. < EOS >这个句子，我们要令$x^{< 1 >}=0$, $x^{< 2 >}=one_ hot(cats)$, $x^{< 3 >}=one_ hot(average)$，……。然后，从第一个输出概率分布$\hat{y}^{< 1 >}$里找出cats对应的概率，去$\hat{y}^{< 2 >}$里找到average对应的概率，去$\hat{y}^{< 3 >}$里找到15对应的概率，以此类推。最后把所有的概率乘起来。

通过这一节，我们学到了RNN的一种应用。是否真正理解语言模型这一任务，并不重要。重要的是，我们学到了RNN是怎么巧妙去完成一项任务的。在完成和序列数据有关的任务时，我们要精心定义RNN的输入序列和输出序列。一旦这两个序列定义好了，训练模型并解决任务就是很轻松的事情。

用语言模型采样出全新的序列

给定一个别人训练好的RNN语言模型，我们可以弄出一个很好玩的应用：生成一个训练集里没有的句子。

我们刚刚学过，在计算一句话的概率时，RNN会把句子里的每一个单词输入，输出单词出现在前几个单词之后的概率分布$\hat{y}$。反过来想，我们可以根据RNN输出的概率分布，随机采样出某一个单词的下一个单词出来。具体来说，我们先随机生成句子里的第一个单词，把它输入RNN。再用RNN生成概率分布，对概率分布采样出下一个单词，采样出一个单词就输入一个单词，直到采样出< EOS >。这个过程就好像是在让AI生成句子一样。

对概率分布采样，其实就是以某种概率随机挑选。比如我有两个骰子，我要计算两个骰子点数之和。这个点数之和就是一个概率分布，掷一轮骰子就是去分布里采样。我们可以快速地算出，点数之和为2的概率是$\frac{1}{36}$, 点数之和为3的概率是$\frac{2}{36}$。也就是说，我们在采样时，有$\frac{1}{36}$的概率取到2，$\frac{2}{36}$的概率取到3。

如果把语料库的最小单元从单词换成字母，句子生成就变成了单词生成，我们可以让AI生成出从没出现过却看上去很合理的单词。

RNN 的梯度问题

在前几门课中，我们曾学过，过深的神经网络会有梯度过大/过小的问题。这些问题在RNN中也存在，毕竟RNN一般都是用来处理很长的序列数据的。

梯度过大的问题倒是有办法解决：设置一个梯度最大值，让所有梯度都不能超过这个值。

梯度过小的问题比较麻烦。想象一个很长的句子:The cat, which ate apples, pears, …., was full.这个cat和was存在着依赖关系。一旦梯度过小，一个句子前后的依赖关系就不是那么好传递了。

下面几节我们会学一些解决梯度问题的架构。

GRU (Gated Recurrent Unit)

我们可以用GRU (Gated Recurrent Unit)来替代标准RNN中的计算单元，以解决梯度问题。

为了明确标准RNN的哪些模块被替换了，我们先回顾一下RNN原来的计算单元。

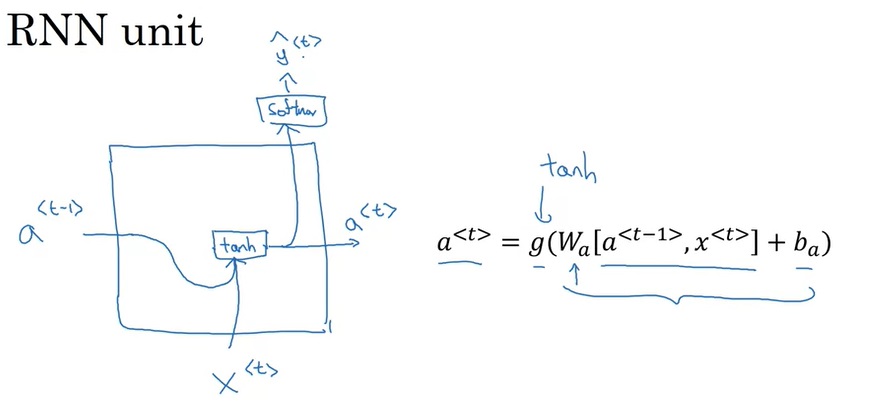
在标准的RNN单元中，$x^{< t >}$和$a^{< t-1 >}$一起决定了$a^{< t >}$，$a^{< t >}$又决定了$\hat{y}^{< t >}$。

先在脑中对这张图有个印象，稍后我们会看到GRU是怎样改进这个计算单元的。

上一节里，我们分析过，梯度消失会导致一句话后面的单词忘掉了前面的单词。那么，可不可以让网络的“记性”更好一点呢？我们可以参考一下人类的记忆行为。比如，当我们在接到了验证码短信后，要把验证码在脑子里记一段时间：读完了短信，要记住验证码；关闭短信应用，要记住验证码；打开需要验证码的应用，要记住验证码；输入验证吗时，要记住验证码；输完了验证码，总算可以忘记验证码了。这个过程中，我们一直在维护“验证码”这个信息，决定是记住它还是忘记它。我们可以让神经网络模型也按照这种思路记忆之前的信息。

在每轮计算更新中间变量$a$时，GRU还要使用到一个新的变量，表示中间变量$a$该不该忘记。这个变量越靠近0，就说明越应该保持之前的中间变量；越靠近1，就越靠近新的$a$。GRU的这个变量起到了电路中逻辑门的效果（GRU的第一个单词是gated）。

具体来说，一个简化版GRU的计算过程用数学符号表示如下：

我们把中间变量$a$临时更名为$c$，表示记忆单元memory cell。和之前的$a$一样，我们每轮要算一个新的$\tilde{c}$：

$$\begin{aligned} \tilde{c}^{< t >} &= tanh(W_{c} [c^{< t - 1 >}, x^{< t >}] + b_c) \end{aligned}$$

而同时，我们还要算一个决定是不是要用$\tilde{c}$去更新过去的$c$的“逻辑门” $\Gamma_u$:

$$\begin{aligned} \Gamma_u &= sigmoid(W_{u} [c^{< t - 1 >}, x^{< t >}] + b_u) \end{aligned}$$

注意，$\Gamma_u$和逻辑门不同，不是真的只能取0或1，而是取0~1中一个中间的值，表示更新的程度。

之后，每一轮的$c^{< t >}$是这样更新的：

$$c^{< t >} = \Gamma_u \ast \tilde{c}^{< t >} + (1 - \Gamma_u) \ast c^{< t - 1 >}$$

它的图示如下，其中紫色部分是更新操作。

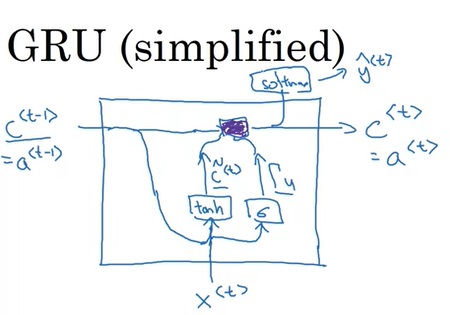
在完整的GRU中，计算公式稍微复杂一点：

$$\begin{aligned} \tilde{c}^{< t >} &= tanh(W_{c} [\Gamma_r \ast c^{< t - 1 >}, x^{< t >}] + b_c) \\ \Gamma_u &= sigmoid(W_{u} [c^{< t - 1 >}, x^{< t >}] + b_u) \\ \Gamma_r &= sigmoid(W_{r} [c^{< t - 1 >}, x^{< t >}] + b_r) \\ c^{< t >} &= \Gamma_u \ast \tilde{c}^{< t >} + (1 - \Gamma_u) \ast c^{< t - 1 >} \end{aligned}$$

唯一的区别是$c^{< t - 1 >}$多过了一道$\Gamma_r$。这种设计的好处很难从理论上解释。当时的研究者试了很多类似的GRU架构，最后发现这样的GRU是效果最好的。

LSTM (long short term memory) 单元

LSTM单元是另一种改进版的RNN单元。LSTM的核心思想和GRU一模一样，也是使用门来控制记忆变量的更新幅度，只是公式更复杂了一点。在LSTM中，要传递的中间变量有两个：$c$和$a$，使用的输出门也从2个增加到了3个。

$$\begin{aligned} \tilde{c}^{< t >} &= tanh(W_{c} [\Gamma_r \ast a^{< t - 1 >}, x^{< t >}] + b_c) \\ \Gamma_u &= sigmoid(W_{u} [a^{< t - 1 >}, x^{< t >}] + b_u) \\ \Gamma_f &= sigmoid(W_{f} [a^{< t - 1 >}, x^{< t >}] + b_f) \\ \Gamma_o &= sigmoid(W_{o} [a^{< t - 1 >}, x^{< t >}] + b_o) \\ c^{< t >} &= \Gamma_u \ast \tilde{c}^{< t >} + \Gamma_f \ast c^{< t - 1 >} \\ a^{< t >} &= \Gamma_o \ast tanh (c^{< t >}) \end{aligned}$$

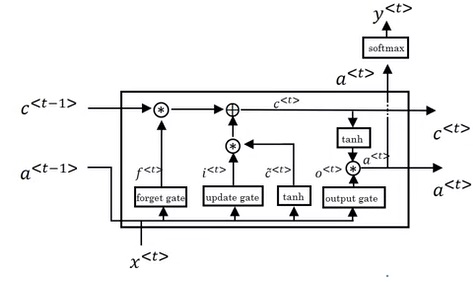
我觉得看图不如看公式看得清楚。

我们不需要刻意去记LSTM的结构，也不要纠结为什么要在哪个地方用哪个门，只需要知道LSTM和GRU的区别，会用它们就行了。

虽然LSTM比GRU更复杂，但实际上LSTM很早（1997年）就有了，GRU是近几年才有的。二者的效果并没有显著的差别，一般认为LSTM功能更强大，GRU计算速度更快。碰到新任务无脑用LSTM即可，而如果要构建较大的网络则可以考虑使用性能更好的GRU。

双向RNN

之前提过，标准的RNN有一个问题：先出现的单词无法获取后续单词的信息。比如句首单词是Teddy，你不知道这是“泰迪熊”还是“泰迪”这个人名。为了解决这个问题，我们可以升级一下RNN的基础架构，使用双向RNN（BRNN）。在这个新架构下，GRU和LSTM的单元可以照用，不受影响。

BRNN的示意图如下：

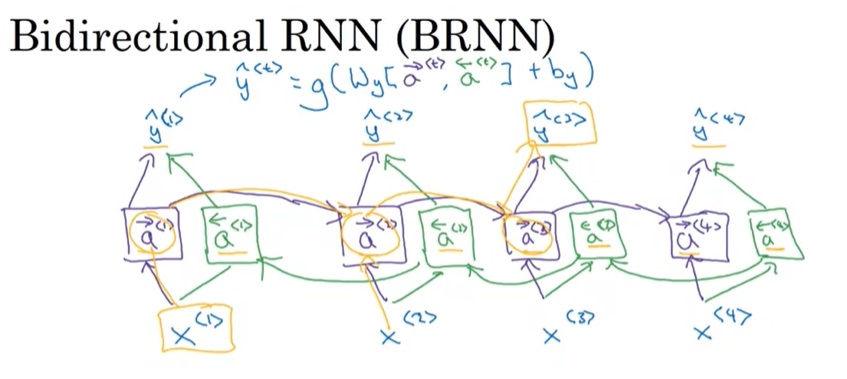
假设一句话有4个单词。在BRNN中，除了会先从1-4正着输入一遍序列外，还会从4-1倒着输入一遍序列。正着传的中间变量叫$\overrightarrow{a}$，倒着传的中间变量叫做$\overleftarrow{a}$。每一轮输出满足$\hat{y}=g(W_y[ \overrightarrow{a}, \overleftarrow{a} ] + b_y)$。

BRNN+LSTM通常是一个新序列任务的标配。当然，BRNN也有一个缺点：必须等一个序列输入完了才能返回结果，而不能实时返回结果。在语音识别等实时性较强的任务里，可能普通RNN更合适一点。

深层RNN

到目前为止，我们学的RNN都是由几个简单的矩阵运算构成的，似乎和这套课的标题“深度学习”不沾边。实际上，也可以给基础的RNN多加一些参数，变成一个深层的RNN。

正如堆叠标准神经网络的隐藏层一样，我们可以堆叠RNN的基础模块，并传递多个中间变量。由于时序计算的计算成本很高，堆3层的计算量就已经很大了。

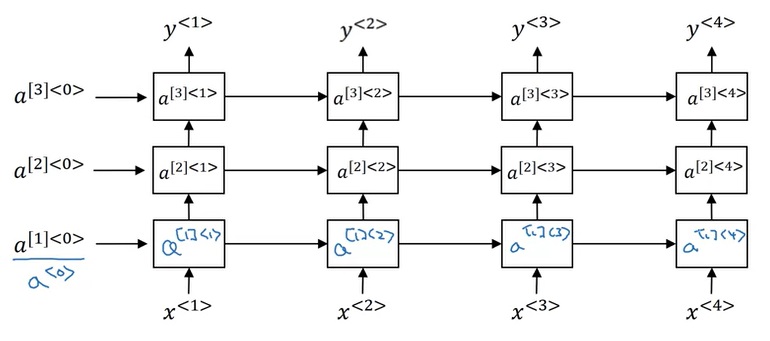
如果想进一步提升网络的拟合能力，可以修改计算输出$y$的结构，堆叠一些非时序的神经网络隐藏层。

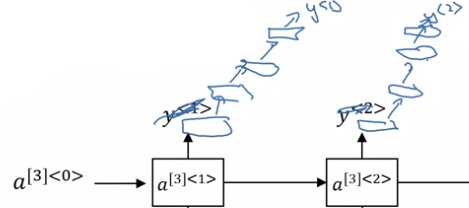
时序模块之所以计算缓慢，一大原因是无法并行。靠后的变量必须等之前的变量算好了才能计算。而在输出$y$的路径中添加一些隐藏层的运算代价没有那么大，因为这些运算是可以并行的。

同样，使用深层RNN时，双向RNN，还有LSTM, GRU都是可以用的。

总结

在这一课里，我们初次认识了序列数据，并学习了处理序列数据的RNN。利用RNN，我们可以开发出许多和序列数据相关的应用。基础的RNN存在不少问题，所以RNN存在着许多改进方法。让我们看一看这一课的具体知识点：

• 序列数据及相关任务的示例

  • 语音识别：输入语音，输出文字
  • 音乐生成：无输入，输出语音
  • 机器翻译：输入某种文字，输出另一种文字
  • 情绪分类：输入文字，输出1-5的分数
  • 命名实体识别：输入文字，输出每个单词是否是命名实体

• 单词的表示

  • 先准备好一个词汇表。比如大小为10000的词汇表（要包括<UNK>, <EOS>）。
  • 每一个单词是一个长度10000的one-hot向量。单词在词汇表中的序号，就是one-hot向量中值为1的下标。

• 循环神经网络（RNN）

  • 基本思想：用$a$表示上文信息
  • 计算流程：循环输入序列元素，维护$a$
  • 计算公式
  • 反向传播的大概流程

• 防止RNN梯度消失：GRU, LSTM

  • 基本思想：选择性更新$a$
  • 大概了解GRU, LSTM的公式
  • GRU, LSTM的使用场景

• 获取下文信息：BRNN

  • 基本思想与结构
  • 使用场景

• 增强表达能力：深层RNN

  • 怎么添加更多层RNN
  • 怎么更好地拟合输出

• RNN应用：语言模型

  • 语言模型的定义
  • 语言模型的训练与推理
  • 对语言模型采样