周弈帆的博客
0%

抛开数学，轻松学懂 VAE（附 PyTorch 实现）

Posted on In ,

变分自编码器（VAE）是一类常见的生成模型。纯VAE的生成效果不见得是最好的，但VAE还是经常会被用作大模型的子模块。即使是在VAE发明多年的今天，学习VAE还是很有必要的。相比GAN等更符合直觉的模型，彻底理解VAE对数学的要求较高。在这篇文章中，我会从计算机科学的角度出发，简明地讲清楚VAE的核心原理，并附上代码实现的介绍。同时，我会稍微提及VAE是怎么利用数学知识的，以及该怎么去拓展了解这些数学知识。

用自编码器生成图像

在正式开始学习VAE之前，我们先探讨一下内容生成的几种方式，并引入自编码器（Autoencoder, AE）这个概念。为了方面描述，我们仅讨论图像的生成。

在设计生成图像的程序之前，我们要考虑一个问题——程序的输入是什么？如果程序没有任何输入，那么它就应该有一个确定的输出，也就是只能画出一幅图片。而只能画出一幅图片的程序没有任何意义的。因此，一个图像生成模型一定要有输入，用于区分不同的图片。哪怕这种输入仅仅是0, 1, 2这种序号也可以，只要模型能看懂输入，为每个输入生成不同的图片就行了。

可是，我们不仅希望不同的输入能区分不同的图片，还要让相近的输入生成相近的图片。比如1.5号图片应该长得和1号和2号相似。为了让模型满足这种性质，我们可以干脆把模型的输入建模成有意义的高维实数向量。这个向量，可以是看成对图像的一种压缩编码。比如(170, 1)就表示一幅身高为170cm的男性的照片。

绝大多数生成模型都是用这种方式对生成过程建模。所有的输入向量$z$来自于一个标准正态分布$Z$。图像生成，就是把图像的编码向量$z$解码成一幅图像的过程。不同的生成模型，只是对这个过程有着不同的约束方式。

自编码器的约束方式十分巧妙：既然把$z$翻译回图像是一个解码的过程，为什么不可以把编码的过程也加进来，让整个过程自动学习呢？如下图所示，我们可以让一个模型（编码器）学会怎么把图片压缩成一个编码，再让另一个模型（解码器）学会怎么把编码解压缩成一幅图片，最小化生成图片与原图片之间的误差。

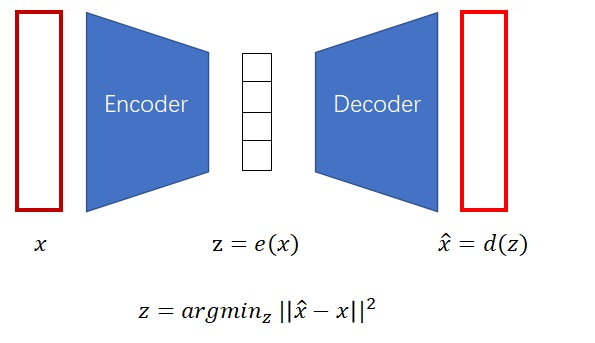
最后，解码器就是我们需要的生成模型。只要在标准多元正态分布里采样出$z$，就可生成图片了。另外，理想情况下，$z$之间的插值向量也能代表在语义上插值的图片。

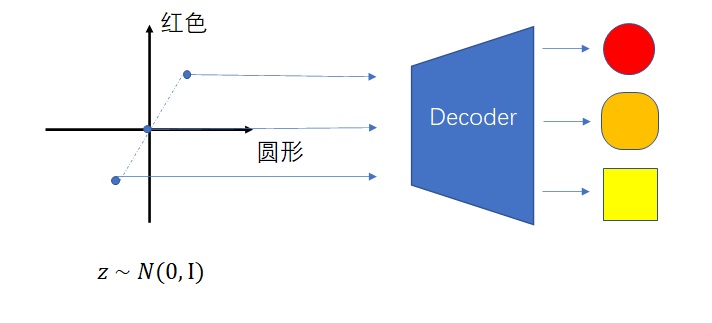
可是，由于自编码器本身的限制，这种理想不一定能实现。

自编码器的问题——过拟合

自编码器的信息压缩能力十分强大。只要编码器和解码器的神经网络足够复杂，所有训练集里的图像都可以被压缩成非常短的编码。这种编码短到什么程度了呢？——只要一个一维向量（实数）就可以描述所有训练集里的图像了。

想做到这一点并不难。还记得我们开头对生成模型的输入的讨论吗？只要让模型把所有图片以数组的形式存到编码器和解码器里，以0, 1, 2这样的序号来表示每一幅训练集里的图片，就能完成最极致的信息压缩。当然，使用这种方式的话，编码$z$就失去了所有的语义信息，编码之间的插值也不能表示图像语义上的插值了。

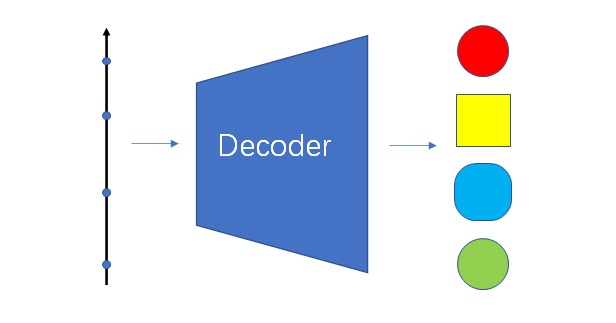
这是由模型过拟合导致的。如果仅使用自编码器本身的约束方式，而不加入其他正则化方法的话，一定会出现过拟合。

VAE——一种正则化的自编码器

VAE就是一种使用了某种正则化方法的自编码器，它解决了上述的过拟合问题。VAE使用的这种方法来自于概率论的变分推理，不过，我们可以在完全不了解变分推理的前提下看懂VAE。

VAE的想法是这样的：我们最终希望得到一个分布$Z$，或者说一条连续的直线。可是，编码器每次只能把图片编码成一个向量，也就是一个点。很多点是很难重建出一条连续的直线的。既然如此，我们可以把每张图片也编码成一个分布。多条直线，就可以比较容易地拼成我们想要的直线了。

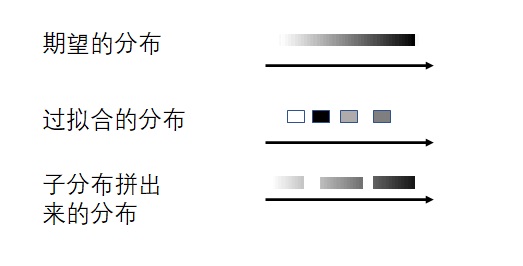
当然，只让模型去拟合分布是不够的。如果各个分布都乱七八糟，相距甚远，那么它们怎么都拼不成一个标准正态分布。因此，我们还需要加上一个约束，让各个分布和标准正态分布尽可能相似。

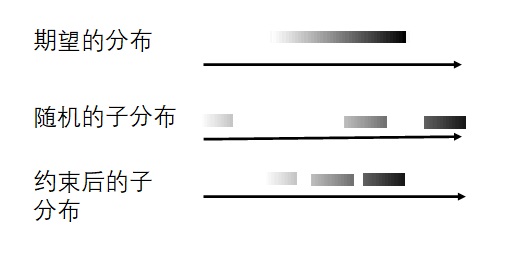
这样，我们可以总结一下VAE的训练框架。VAE依然使用了编码器-解码器的架构。只不过，编码器的输出是一个可学习的正态分布。对分布是不可能做求导和梯度下降的，但我们可以去分布里采样，对采样出来的编码$z$解码并求导。

另外，VAE的损失函数除了要最小化重建图像与原图像之间的均方误差外，还要最大化每个分布和标准正态分布之间的相似度。

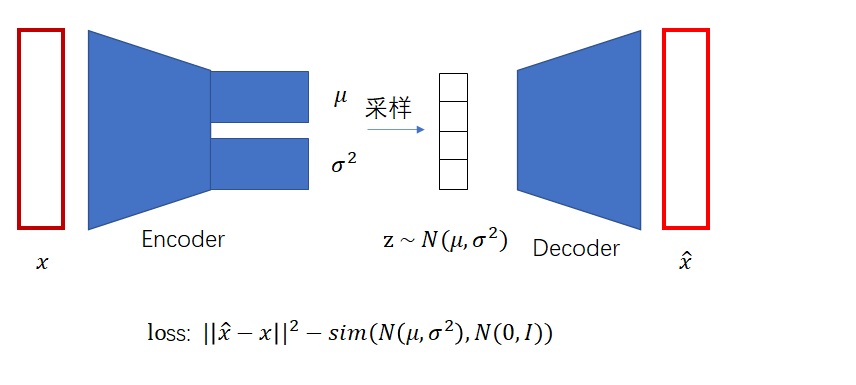
常见的描述分布之间相似度的指标叫做KL散度。只要把KL散度的公式套进损失函数里，整个训练框架就算搭好了。

如果你对KL散度的原理感兴趣，欢迎阅读我的上一篇文章：从零理解熵、交叉熵、KL散度

VAE的原理其实就是这么简单。总结一下，VAE本身是一个编码器-解码器结构的自编码器，只不过编码器的输出是一个分布，而解码器的输入是该分布的一个样本。另外，在损失函数中，除了要让重建图像和原图像更接近以外，还要让输出的分布和标准正态分布更加接近。

VAE 与变分推理

前几段其实只对VAE做了一个直觉上的描述，VAE的损失函数实际上是经严谨的数学推导得到的。如果你对数学知识不感兴趣，完全可以跳过这一节的讲解。当然，这一节也只会简单地描述VAE和变分推理的关系，更详细的数学推导可以去参考网上的其他文章。

让我们从概率论的角度看待生成模型。生成模型中的$z$可以看成是隐变量，它决定了能观测到的变量$x$。比如说，袋子里有黑球和白球，你不断地从袋子里取球出来再放回去，就能够统计出抽到黑球和白球的频率。然而，真正决定这个频率的，是袋子里黑球和白球的数量，这些数量就是观测不到的隐变量。简单来说，隐变量$z$是因，变量$x$是果。

生成模型，其实就是假设$z$来自标准正态分布，想要拟合分布$P(x|z)$（解码器），以得到$x$的分布（图像分布）。为了训练解码器，自编码器架构使用了一个编码器以描述$P(z|x)$。这样，从训练集里采样，等于是采样出了一个$x$。根据$P(z|x)$求出一个$z$，再根据$P(x|z)$试图重建$x$。优化这个过程，就是在优化编码器和解码器，也就是优化$P(z|x)$和$P(x|z)$。

然而，$P(z|x)$和$P(x|z)$之间有一个约束，它们必须满足贝叶斯公式：

假如我们要用一个和$x$有关的关于$z$的分布$Q_x(z)$去拟合$P(z|x)$，就要让$Q_x(z)$和$\frac{P(x|z)P(z)}{P(x)}$这两个分布尽可能相似。如果这个相似度是KL散度，经过一系列的推导，就可以推导出我们在VAE里使用的那个损失函数。

简单来说，拟合一个未知分布的技术就叫做变分推理。VAE利用变分推理，对模型的编码器和解码器加了一个约束，这个约束在化简后就是VAE的损失函数。

VAE和变分推理的关系就是这样。如果还想细究，可以去先学习KL散度相关的知识，再去看一下VAE中KL散度的公式推导。当然，不懂这些概念并不影响VAE的学习。

总结

VAE其实就是一个编码器-解码器架构，和U-Net以及部分NLP模型类似。然而，为了抑制自编码过程中的过拟合，VAE编码器的输出是一个正态分布，而不是一个具体的编码。同时，VAE的损失函数除了约束重建图像外，还约束了生成的分布。在这些改进下，VAE能够顺利地训练出一个解码器，以把来自正态分布的随机变量$z$画成一幅图像。

如果你想通过代码实践进一步加深对VAE的理解，可以阅读附录。

参考资料

  1. 一篇不错的VAE讲解。我是跟着这篇文章学习的。https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
  2. 我的VAE PyTorch实现参考了这个仓库：https://github.com/AntixK/PyTorch-VAE 。开头的人脸生成效果图是从这个项目里摘抄过来的。

VAE PyTorch 实现

项目网址：https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/VAE

数据集

在这个项目中，我使用了CelebA数据集。这个数据集有200k张人脸，裁剪和对齐后的图片只有1个多G，对实验非常友好。

CelebA的下载链接可以在官方网站上找到：https://mmlab.ie.cuhk.edu.hk/projects/CelebA.html。

下载好了图片后，可以用下面的代码创建Dataloader。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import os

import torch
from PIL import Image
from torch.utils.data import DataLoader, Dataset
from torchvision import transforms


class CelebADataset(Dataset):
    def __init__(self, root, img_shape=(64, 64)) -> None:
        super().__init__()
        self.root = root
        self.img_shape = img_shape
        self.filenames = sorted(os.listdir(root))

    def __len__(self) -> int:
        return len(self.filenames)

    def __getitem__(self, index: int):
        path = os.path.join(self.root, self.filenames[index])
        img = Image.open(path).convert('RGB')
        pipeline = transforms.Compose([
            transforms.CenterCrop(168),
            transforms.Resize(self.img_shape),
            transforms.ToTensor()
        ])
        return pipeline(img)


def get_dataloader(root='data/celebA/img_align_celeba', **kwargs):
    dataset = CelebADataset(root, **kwargs)
    return DataLoader(dataset, 16, shuffle=True)

这段代码是一段非常常规的根据图片路径读取图片的代码。只有少数地方需要说明：

  • 为了尽快完成demo，所有人脸图片的分辨率都是$64 \times 64$。
  • CelebA里裁剪后的人脸图片是长方形的。要先调用CenterCrop裁剪出正方形人脸，再做Resize。

为了验证Dataloader的正确性，我们可以写一些脚本来查看Dataloader里的一个batch的图片。

1
2
3
4
5
6
7
8
9
10
11
12
13
if __name__ == '__main__':
    dataloader = get_dataloader()
    img = next(iter(dataloader))
    print(img.shape)
    # Concat 4x4 images
    N, C, H, W = img.shape
    assert N == 16
    img = torch.permute(img, (1, 0, 2, 3))
    img = torch.reshape(img, (C, 4, 4 * H, W))
    img = torch.permute(img, (0, 2, 1, 3))
    img = torch.reshape(img, (C, 4 * H, 4 * W))
    img = transforms.ToPILImage()(img)
    img.save('work_dirs/tmp.jpg')

这段代码使用了一些小技巧。首先，next(iter(dataloader))可以访问Dataloader的第一个数据。其次，在把一个batch的图片转换成图片方格的过程中，我使用了比较骚的换维度、换形状操作，看起来很帅。

模型

我的VAE模型使用了类似U-Net的操作：编码器用卷积把图像的边长减半，通道翻倍，解码器用反卷积把图像的边长翻倍，通道减半。

模型结构的定义函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import torch
import torch.nn as nn


class VAE(nn.Module):
    '''
    VAE for 64x64 face generation. The hidden dimensions can be tuned.
    '''
    def __init__(self, hiddens=[16, 32, 64, 128, 256], latent_dim=128) -> None:
        super().__init__()

        # encoder
        prev_channels = 3
        modules = []
        img_length = 64
        for cur_channels in hiddens:
            modules.append(
                nn.Sequential(
                    nn.Conv2d(prev_channels,
                              cur_channels,
                              kernel_size=3,
                              stride=2,
                              padding=1), nn.BatchNorm2d(cur_channels),
                    nn.ReLU()))
            prev_channels = cur_channels
            img_length //= 2
        self.encoder = nn.Sequential(*modules)
        self.mean_linear = nn.Linear(prev_channels * img_length * img_length,
                                     latent_dim)
        self.var_linear = nn.Linear(prev_channels * img_length * img_length,
                                    latent_dim)
        self.latent_dim = latent_dim
        # decoder
        modules = []
        self.decoder_projection = nn.Linear(
            latent_dim, prev_channels * img_length * img_length)
        self.decoder_input_chw = (prev_channels, img_length, img_length)
        for i in range(len(hiddens) - 1, 0, -1):
            modules.append(
                nn.Sequential(
                    nn.ConvTranspose2d(hiddens[i],
                                       hiddens[i - 1],
                                       kernel_size=3,
                                       stride=2,
                                       padding=1,
                                       output_padding=1),
                    nn.BatchNorm2d(hiddens[i - 1]), nn.ReLU()))
        modules.append(
            nn.Sequential(
                nn.ConvTranspose2d(hiddens[0],
                                   hiddens[0],
                                   kernel_size=3,
                                   stride=2,
                                   padding=1,
                                   output_padding=1),
                nn.BatchNorm2d(hiddens[0]), nn.ReLU(),
                nn.Conv2d(hiddens[0], 3, kernel_size=3, stride=1, padding=1),
                nn.ReLU()))
        self.decoder = nn.Sequential(*modules)

首先来看编码器的部分。每个卷积模块由卷积、BN、ReLU构成。卷完了再用两个全连接层分别生成正态分布的均值和方差。注意，卷积完成后，图像的形状是[prev_channels, img_length, img_length]，为了把它输入到全连接层，我们到时候会做一个flatten操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# encoder
        prev_channels = 3
        modules = []
        img_length = 64
        for cur_channels in hiddens:
            modules.append(
                nn.Sequential(
                    nn.Conv2d(prev_channels,
                              cur_channels,
                              kernel_size=3,
                              stride=2,
                              padding=1), nn.BatchNorm2d(cur_channels),
                    nn.ReLU()))
            prev_channels = cur_channels
            img_length //= 2
        self.encoder = nn.Sequential(*modules)
        self.mean_linear = nn.Linear(prev_channels * img_length * img_length,
                                     latent_dim)
        self.var_linear = nn.Linear(prev_channels * img_length * img_length,
                                    latent_dim)
        self.latent_dim = latent_dim

解码器和编码器的操作基本完全相反。由于隐变量的维度是latent_dim，需要再用一个全连接层把图像的维度投影回[prev_channels, img_length, img_length]。之后就是反卷积放大图像的过程。写这些代码时一定要算好图像的边长，定好反卷积的次数，并且不要忘记最后把图像的通道数转换回3。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# decoder
modules = []
self.decoder_projection = nn.Linear(
    latent_dim, prev_channels * img_length * img_length)
self.decoder_input_chw = (prev_channels, img_length, img_length)
for i in range(len(hiddens) - 1, 0, -1):
    modules.append(
        nn.Sequential(
            nn.ConvTranspose2d(hiddens[i],
                                hiddens[i - 1],
                                kernel_size=3,
                                stride=2,
                                padding=1,
                                output_padding=1),
            nn.BatchNorm2d(hiddens[i - 1]), nn.ReLU()))
modules.append(
    nn.Sequential(
        nn.ConvTranspose2d(hiddens[0],
                            hiddens[0],
                            kernel_size=3,
                            stride=2,
                            padding=1,
                            output_padding=1),
        nn.BatchNorm2d(hiddens[0]), nn.ReLU(),
        nn.Conv2d(hiddens[0], 3, kernel_size=3, stride=1, padding=1),
        nn.ReLU()))
self.decoder = nn.Sequential(*modules)

网络前向传播的过程如正文所述，先是用编码器编码，把图像压平送进全连接层得到均值和方差，再用randn_like随机采样，把采样的z投影、变换成正确的维度，送入解码器，最后输出重建图像以及正态分布的均值和方差。

1
2
3
4
5
6
7
8
9
10
11
12
13
def forward(self, x):
    encoded = self.encoder(x)
    encoded = torch.flatten(encoded, 1)
    mean = self.mean_linear(encoded)
    logvar = self.var_linear(encoded)
    eps = torch.randn_like(logvar)
    std = torch.exp(logvar / 2)
    z = eps * std + mean
    x = self.decoder_projection(z)
    x = torch.reshape(x, (-1, *self.decoder_input_chw))
    decoded = self.decoder(x)

    return decoded, mean, logvar

用该模型随机生成图像的过程和前向传播的过程十分类似，只不过$z$来自于标准正态分布而已，解码过程是一模一样的。

1
2
3
4
5
6
def sample(self, device='cuda'):
    z = torch.randn(1, self.latent_dim).to(device)
    x = self.decoder_projection(z)
    x = torch.reshape(x, (-1, *self.decoder_input_chw))
    decoded = self.decoder(x)
    return decoded

主函数

在主函数中，我们要先完成模型训练。在训练前，还有一件重要的事情要做：定义损失函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from time import time

import torch
import torch.nn.functional as F
from torchvision.transforms import ToPILImage

from dldemos.VAE.load_celebA import get_dataloader
from dldemos.VAE.model import VAE

# Hyperparameters
n_epochs = 10
kl_weight = 0.00025
lr = 0.005


def loss_fn(y, y_hat, mean, logvar):
    recons_loss = F.mse_loss(y_hat, y)
    kl_loss = torch.mean(
        -0.5 * torch.sum(1 + logvar - mean**2 - torch.exp(logvar), 1), 0)
    loss = recons_loss + kl_loss * kl_weight
    return loss

如正文所述，VAE的loss包括两部分：图像的重建误差和分布之间的KL散度。二者的比例可以通过kl_weight来控制。

KL散度的公式直接去网上照抄即可。

这里要解释一下，我们的方差为什么使用其自然对数logvar。经过我的实验，如果让模型输出方差本身的话，就要在损失函数里对齐取一次自然对数。如果方差很小，趋于0的话，方差的对数就趋于无穷。这表现在loss里会出现nan。因此，在神经网络中我们应该避免拟合要取对数的数，而是直接去拟合其对数运算结果。

准备好了损失函数，剩下就是常规的训练操作了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def train(device, dataloader, model):
    optimizer = torch.optim.Adam(model.parameters(), lr)
    dataset_len = len(dataloader.dataset)

    begin_time = time()
    # train
    for i in range(n_epochs):
        loss_sum = 0
        for x in dataloader:
            x = x.to(device)
            y_hat, mean, logvar = model(x)
            loss = loss_fn(x, y_hat, mean, logvar)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            loss_sum += loss
        loss_sum /= dataset_len
        training_time = time() - begin_time
        minute = int(training_time // 60)
        second = int(training_time % 60)
        print(f'epoch {i}: loss {loss_sum} {minute}:{second}')
        torch.save(model.state_dict(), 'dldemos/VAE/model.pth')

训练好模型后，想要查看模型重建数据集图片的效果也很简单，去dataloader里采样、跑模型、后处理结果即可。

1
2
3
4
5
6
7
8
9
10
def reconstruct(device, dataloader, model):
    model.eval()
    batch = next(iter(dataloader))
    x = batch[0:1, ...].to(device)
    output = model(x)[0]
    output = output[0].detach().cpu()
    input = batch[0].detach().cpu()
    combined = torch.cat((output, input), 1)
    img = ToPILImage()(combined)
    img.save('work_dirs/tmp.jpg')

想用模型随机生成图片的话，可以利用之前写好的模型采样函数。

1
2
3
4
5
6
def generate(device, model):
    model.eval()
    output = model.sample(device)
    output = output[0].detach().cpu()
    img = ToPILImage()(output)
    img.save('work_dirs/tmp.jpg')

在3090上跑这个实验，100个epoch需要5个多小时。但是，模型差不多在10多个epoch的时候就收敛了。

最朴素的VAE的重建效果并不是很好，只能大概看出个脸型。这可能也和我的模型参数较少有关。

随机生成的图片也是形状还可以，但非常模糊。