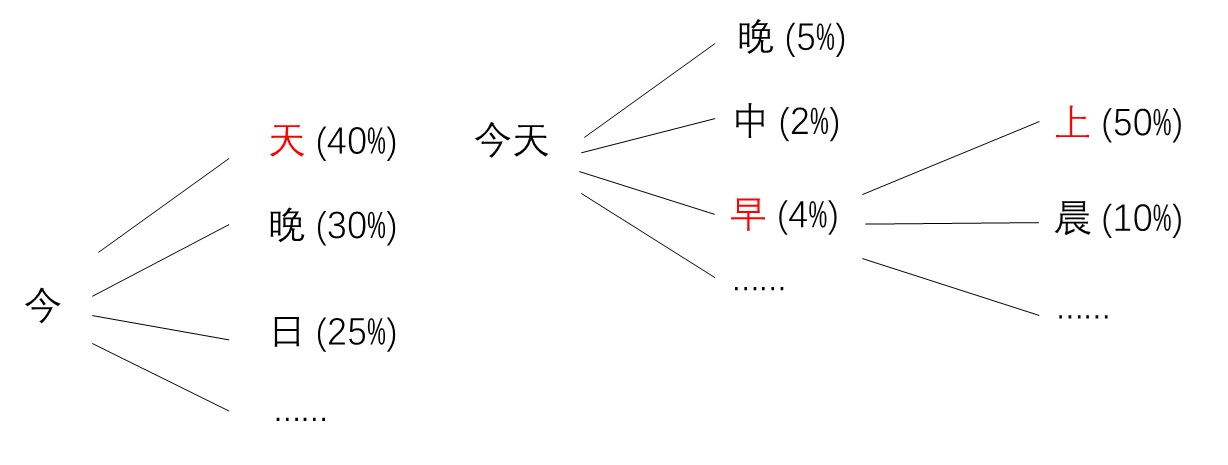
解读何恺明新作：不用向量离散化的自回归图像生成（Autoregressive Image Generation without Vector Quantization）

自回归是一种根据之前已生成内容，不断递归预测下一项要生成的内容的生成模型。这种生成方式十分易懂，符合我们对生活的观察。比如我们希望模型生成一句话，第一个是「今」字，那么第二个字很可能就是「天」字。如果前三个字是「今天早」，那么第四个字就很可能是「上」。

（空）  -> 今
今      -> 天
今天    -> 早
今天早  -> 上

为这种自回归模型的而设计的 Transformer 网络在自然语言处理（NLP）中取得了极大的成功。然而，尽管许多人也尝试用它生成图像，自回归模型却一直没有成为最强大、最受欢迎的图像生成模型。

为了解决此问题，何恺明团队公布了论文 Autoregressive Image Generation without Vector Quantization。作者分析了目前最常见的自回归图像生成模型后，发现模型中的向量离散化 (Vector Quantization, VQ) 是拖累模型能力的罪魁祸首。作者用一些巧妙的方法绕过了 VQ，最终设计出了一种新式自回归模型。该模型在图像生成任务上表现出色，在 ImageNet 图像生成指标上不逊于最先进的图像扩散模型。在这篇博文中，我们就来学习一下这种新颖的无 VQ 自回归图像生成模型。

建议读者在阅读本文前熟悉 VQ-VAE、Transformer、DDPM 等经典工作，了解 NLP 和图像生成中连续值和离散值的概念。可以参考我之前写的文章：

轻松理解 VQ-VAE：首个提出 codebook 机制的生成模型

VQGAN 论文与源码解读：前Diffusion时代的高清图像生成模型

Transformer 论文精读

扩散模型(Diffusion Model)详解：直观理解、数学原理、PyTorch 实现

Stable Diffusion 解读（一）：回顾早期工作

知识回顾

连续值与离散值

在计算机科学中，我们既会用到连续值，也会用到离散值。比如颜色就是一个常见的连续值，我们用 0~1 之间的实数表示灰度从全黑到全白。而词元 (token) 需要用离散值表示，比如我们用 “0” 表示字母 “A”，”1” 表示 “B”, “2” 表示 “C”，并不代表 “B” 是「’A’ 和 ‘C’ 的平均值」。离散值的数值只是用来区分不同概念的。

神经网络默认输入是连续变化的。因此，一个连续值可以直接输入进网络。而代表离散值的整数不能直接输入网络，需要先过一个嵌入层，再正常输入进网络。

自回归与类别分布

在自回归文本生成模型中，为了不断预测下一个词元，通常的做法是用一个神经网络建模下一个词元的类别分布（categorical distribution）。如下面的例子所示，所谓类别分布，就是下一步选择每一个词元的概率。有了概率分布后，我们就能用采样算法采样出下一个词元。

要训练这个预测模型也很简单。每次预测下一个词元的类别分布，其实就是一个分类任务。我们直接照着分类任务的做法，以数据集里现有句子为真值，用交叉熵损失函数就能训练这个预测模型了。

自回归图像生成

由于 Transformer 在 NLP 中的成功，大家也想用 Transformer 做图像生成。在用自回归模型生成图像时，需要考虑图像和文本的两个区别：

文本是一维的，天然有先后顺序以供自回归生成。而图像是二维的，没有先后顺序。
图像的颜色值是连续而非离散的。而只有离散值才能用类别分布表示。

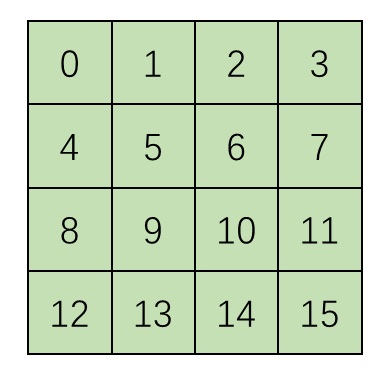
解决问题 1 的方法很简单：没有先后顺序，我们就人工定义一个先后顺序就好了，比如从左上到右下给图像编号。

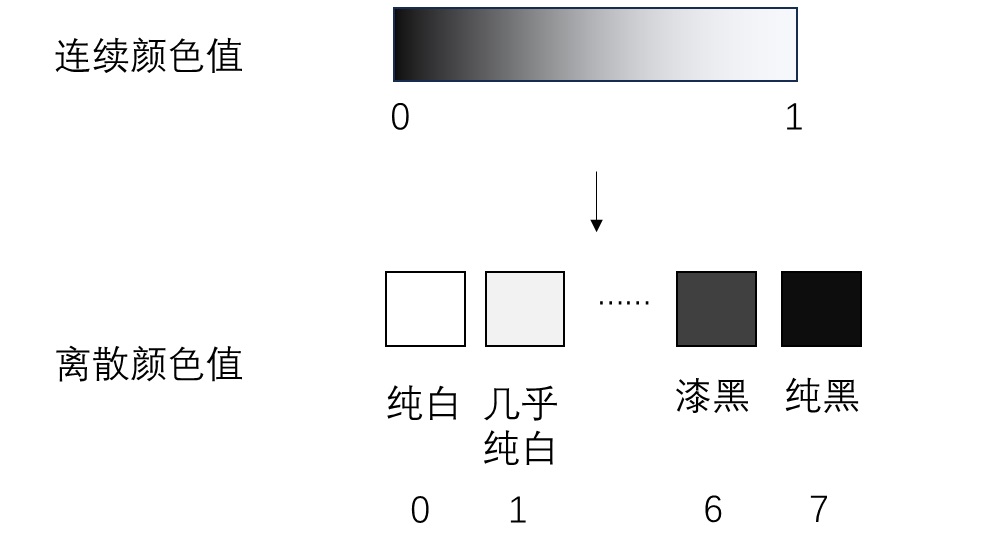
而对于问题 2，一种最简单的方式是把连续的颜色值离散化。比如将原来 0 ~ 1 的灰度值转换为「0 号灰度」、「1 号灰度」、…… 「7号灰度」。神经网络像对待词元一样对待这些灰度值，不知道它们之间的大小关系，只知道生成图像的颜色只能由这 8 种「颜色词语」构成。

向量离散化

把颜色值离散化后，我们的确可以用自回归做图像生成了。但是，由于图像的像素数比文章的词元数要多很多，这种逐像素生成方式会非常慢。为了加速自回归生成，VQ-VAE, VQGAN 等工作借由向量离散化自编码器（VQ 自编码器）实现了一个两阶段的图像生成方法：

训练时，先训练一个包括编码器 (encoder) 和解码器 (decoder) 两个子模型的 VQ 自编码器，再训练一个生成压缩图像的自回归模型。
生成时，先用自回归模型生成出一个压缩图像，再用 VQ 自编码器将其复原成真实图像。

相比普通的自编码器，VQ 自编码器有一项特点：它生成的压缩图像仅由离散值组成。这样，它就同时完成了两项任务，使得自回归模型能够高效地实现图像生成：1）将连续图像变成离散图像；2）减少要生成的像素数。

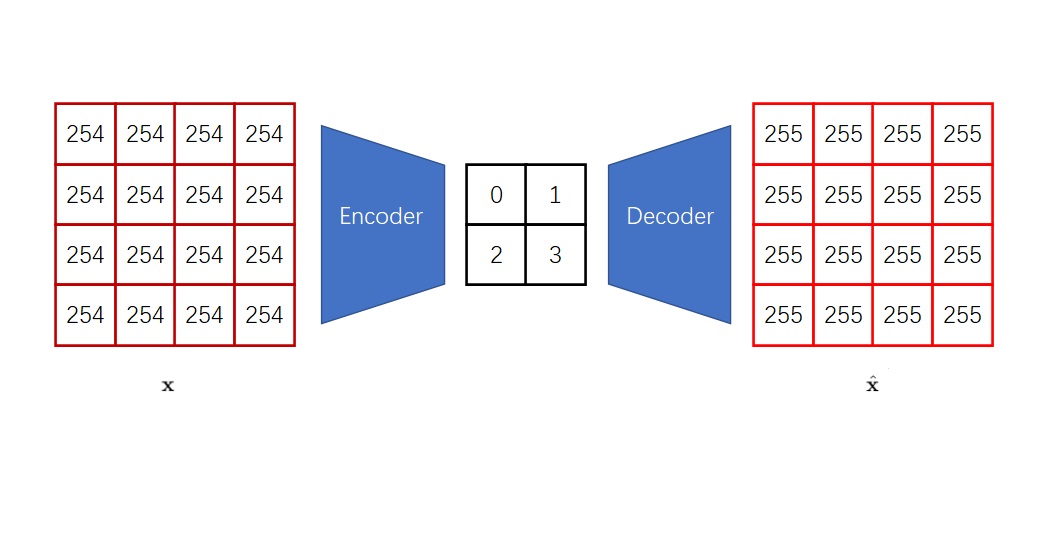
如果你还是不太理解 VQ 的作用，请先回顾 VQ-VAE 工作，再来学习这篇工作。

抛弃 VQ，拥抱扩散模型

我们来总结一下为什么要使用基于 VQ 的自回归图像生成：大家想用基于 Transformer 的自回归模型做图像生成。自回归模型在预测下一个词元/像素时，通常会用一个类别分布来建模下一项数据。由于类别分布只能描述离散数据，而图像又是连续数据，我们需要把连续像素值变成离散值。一种常用的将连续图像变成离散图像的方法是 VQ 自编码器，它既能减少图像尺寸以提高生成效率，又能将连续图像变成离散图像。

但相比普通的自编码器，如 VAE，VQ 自编码器有着一些缺点：

VQ 自编码器很难训练
VQ 自编码器的重建效果没有 VAE 好。比如在 Stable Diffusion 中，开发者选择了用 VAE 而不是 VQ-VAE 作为自编码器

出于抛弃 VQ 的想法，论文的作者发问道：「自回归图像生成真的需要和 VQ 绑定起来吗？」注意到，在我们刚刚阐述使用 VQ 自回归生成的动机时，用了几个「通常」、「常用」这样的非肯定词。这表明我们的这条推理链不是必然的。要取代 VQ，我们可以从两个方面入手：

换一种更强力的把连续图像变成离散图像的方法
从更根本处入手，不用类别分布来建模下一项数据

论文的作者选择了第二种做法：不就是建模一个像素值的分布吗？我们为什么要用死板的类别分布呢？既然扩散模型如此强大，能够拟合复杂的图像分布，那用它来拟合一个像素值的分布还不是轻轻松松？论文的核心思想也就呼之欲出了：用扩散模型而不是类别分布来建模自回归模型中下一个像素值的分布，从而抛弃自编码器里的 VQ 操作，提升模型能力。

可能读者第一次看到这个想法时会有些疑惑：扩散模型不是用来生成一整张图像的吗？它怎么建模一个像素值的分布？它和自回归模型又有什么关系？我们来多花点时间深入理解这个想法。

在文本自回归生成中，输入是已生成文本，输出是下一个词元的类别分布。

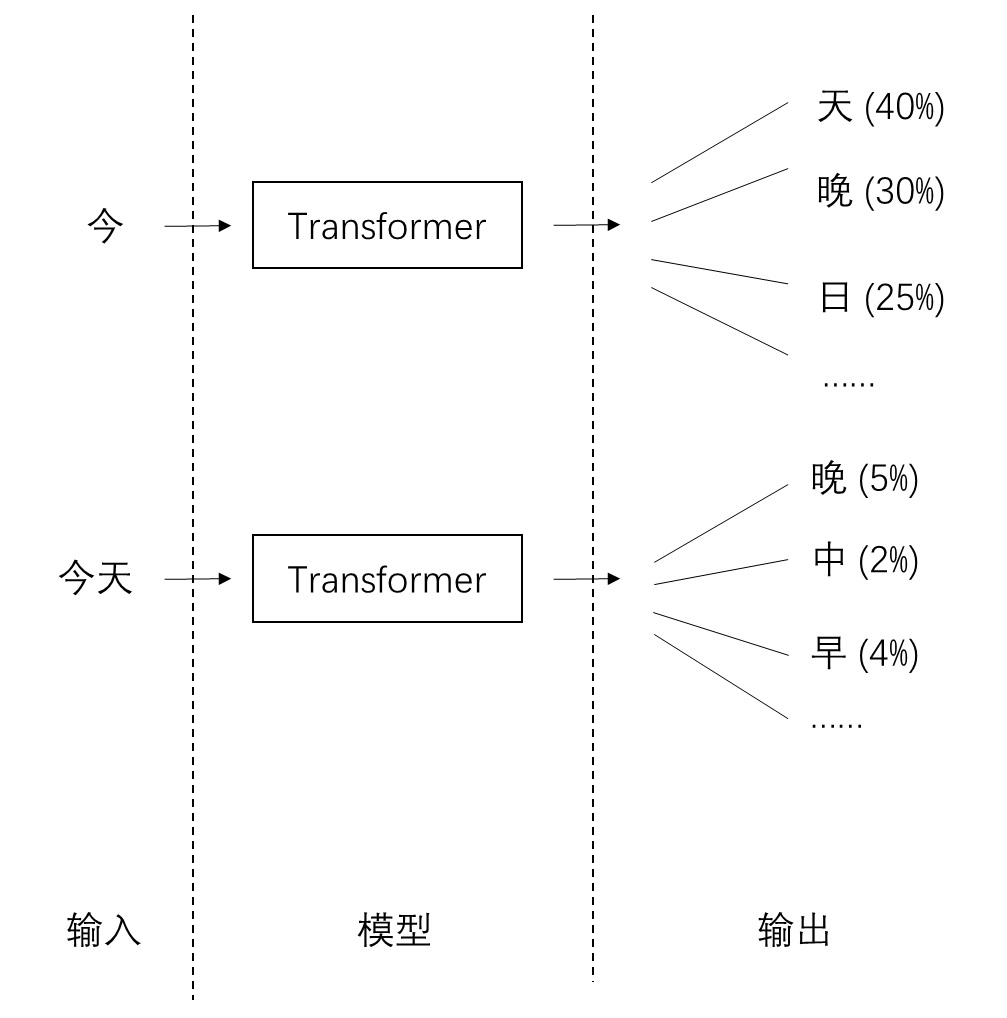
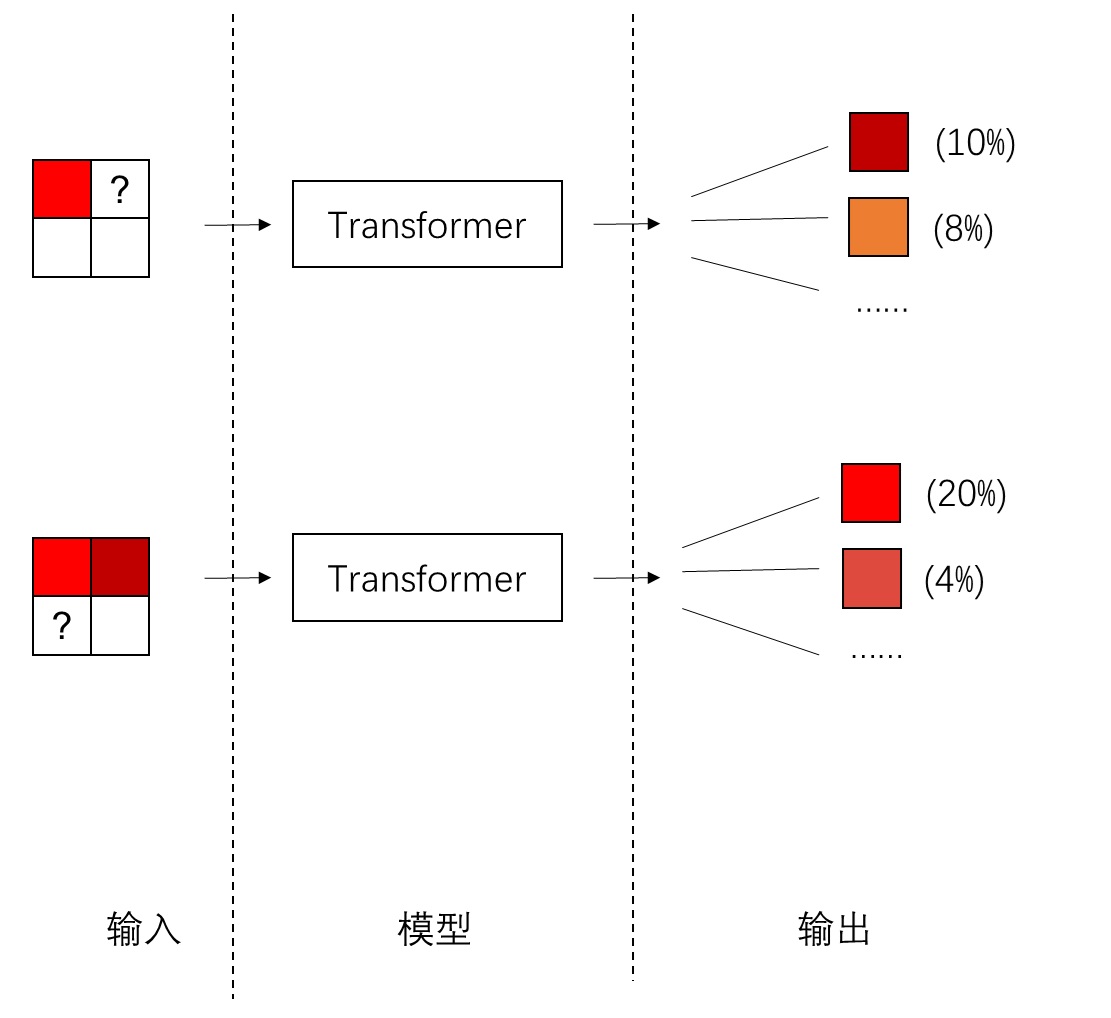
而在图像自回归生成中，输入是已生成像素，输出是下一个像素的类别分布。现在，我们希望不用类别分布，而用另一种方式，根据之前的像素生成出下一个像素。

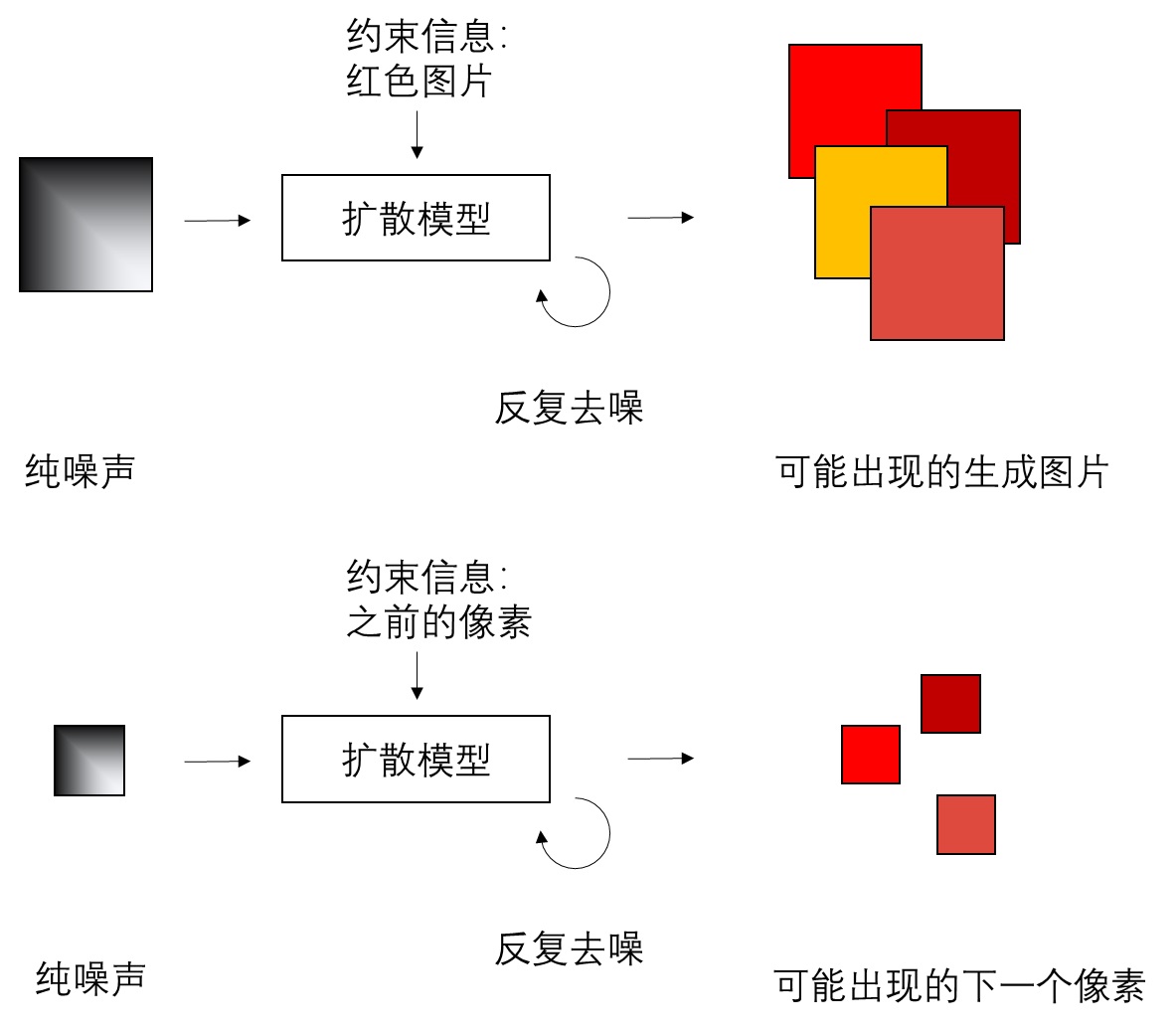
论文作者从扩散模型中获取了灵感。扩散模型是一种强力的生成模型，它可以不根据任何信息，或根据类别、文本等信息，隐式建模训练集的图像分布，从而生成符合训练集分布的图像。既然扩散模型能够建模复杂的图像分布，那它也可以根据之前像素的信息，建模下一个像素的分布。

那么，在这种新式自回归模型里，我们可以用约束于 Transformer 输出的上下文信息的扩散模型来建模下一个像素的分布，尽管现在我们并不知道每种颜色出现的概率。

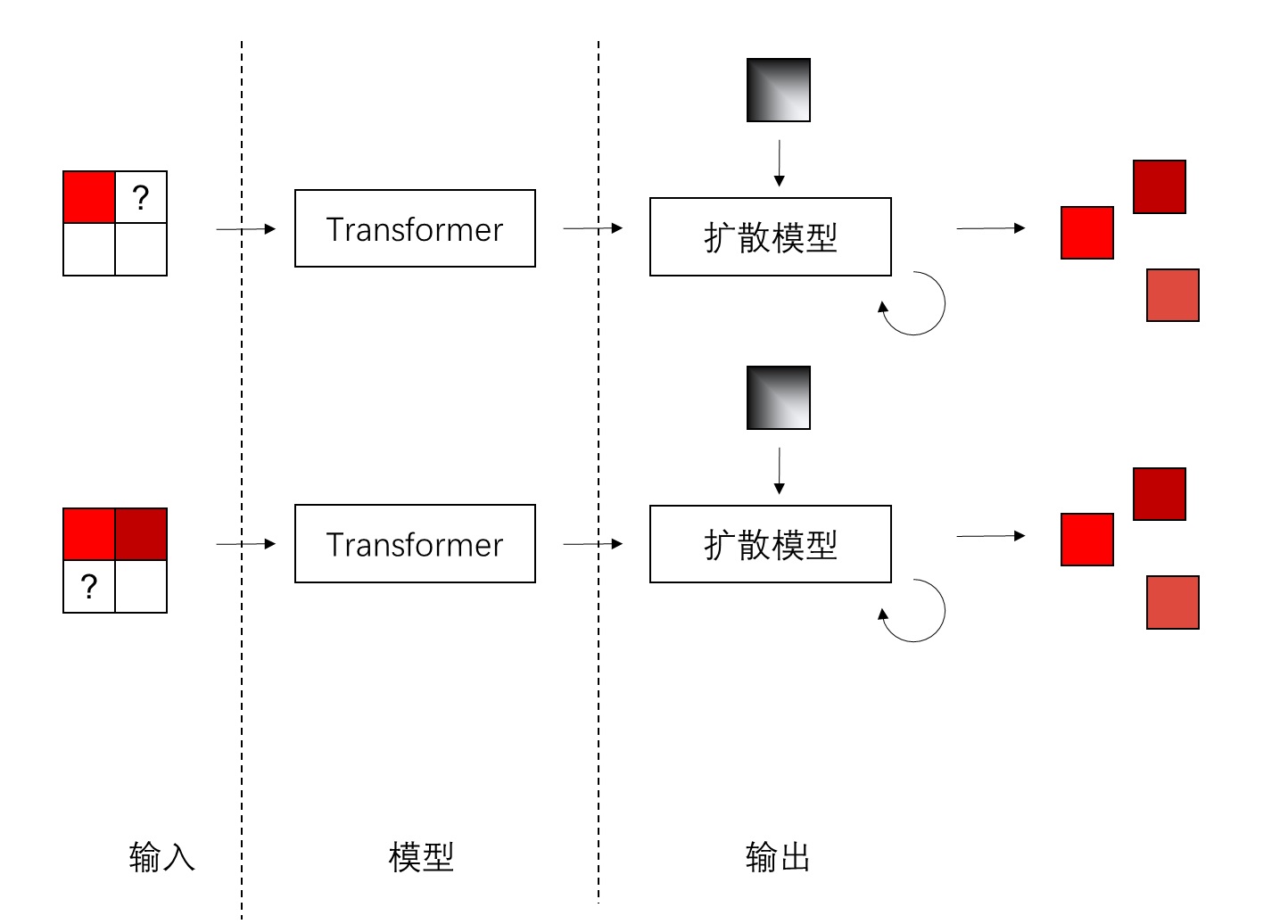
这样做的好处是，以前我们只能用离散的有限类型的颜色（准确来说是图像词元）来表示图像，现在我们能够用连续值来表示图像。模型能够更加轻松地生成内容丰富的图像。

当然，抛弃了 VQ 后，自回归模型确实不需要 VQ 自编码器来把连续图像变成离散图像了。但是，我们依然需要用自编码器来压缩图像，减少要生成的像素数。本工作依然采取了 VQ-VAE、VQGAN 那种两阶段的生成方式，只不过把 VQ 自编码器换成了用 KL loss 约束的 VAE。

训练这种扩散模型的方法很简单。在每一步训练时，我们知道上下文像素是什么，也知道当前像素的真值是什么。那么，只要以上下文像素为约束，用当前像素的真值去训练一个带约束扩散模型就行了。作者把训练这种隐式描述下一个像素值分布的误差函数称为 Diffusion Loss。

具体来说，本工作使用了最基础的带约束 DDPM 扩散模型。它和标准 DDPM 的唯一区别在于误差函数多了一个约束信息 $z$，该信息是上下文像素过 Transformer 的输出。

$L(z, x) = \mathbb{E}_{\epsilon}[||\epsilon-\epsilon_{\theta}(x_t|t, z)||^2]$

$t$ 时刻的噪声图像 $x_t$也是由 DDPM 加噪公式得来的。

$x_t = \sqrt{\bar{\alpha_t}} x + \sqrt{1 - \bar{\alpha_t}} \epsilon$

Diffusion Loss 不仅可以用来训练表示分布的扩散模型，还可以训练前面提取上下文信息的 Transformer。由于约束信息 $z$ 来自 Transformer，可以把 Diffusion Loss 的梯度通过 $z$ 回传到 Transformer 的参数里。

扩散模型的采样公式也和 DDPM 的一样，这里不再赘述。特别地，以前的自回归模型在使用类别分布时，会用温度来控制采样的多样性。为了在扩散模型中也加入类似的温度参数，本工作参考了 Diffusion models beat GANs on image synthesis 论文的有关设计。

在具体模型超参数上，本工作的 DDPM 训练时有 1000 步，采样时有 100 步。乍看之下，DDPM 会为整个生成模型增加许多计算量，但由于只需要建模一个像素的分布，这套模型的 DDPM 可以用非常轻量级的结构。默认配置下，这套模型的 DDPM 的去噪模型是一个由 3 个残差块组成小型 MLP。每个残差块由 LayerNorm、线性层、SiLU、线性层组成。约束信息 $z$ 会和时刻 $t$ 的编码加在一起，用 DiT (Scalable diffusion models with Transformers) 里的 AdaLN 约束机制输入进 LayerNorm 层里。

套用更先进的自回归模型

仅是去掉 VQ，把 Diffusion Loss 加进标准自回归模型，并不能得到一个很好的图像生成模型。于是，作者用更加先进的一些自回归模型（掩码生成模型 Masked Gernerative Models，如 MaskGIT: Masked generative image Transformer、MAGE: Masked generative encoder to unify representation learning and image synthesis）代替标准自回归模型，极大提升了模型的生成能力。

双向注意力

在标准 Transformer 中（如下图 (a) causal 所示），每一个词元只能看到自己及之前词元的信息。这样做的好处是模型能够并行训练，串行推理。训练和推理的速度都会比较快。但是，由于每个词元看不到后面词元的信息，Transformer 提取整个句子（图像）特征的能力会下降。

而 MAE (Masked autoencoders are scalable vision learners) 论文提出了一种双向注意力机制，它可以让词元两两之间都传递信息。但是，这样模型就不能用同一个句子并行训练了，也失去了 KV cache 加速推理的手段。

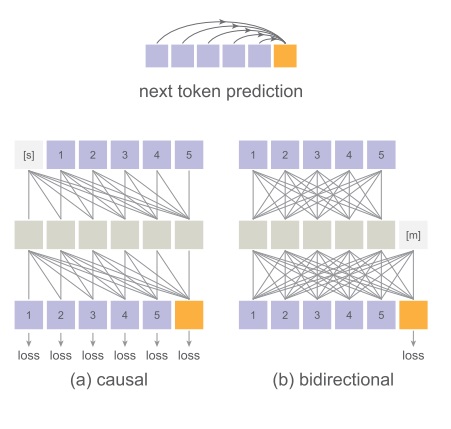
如果你不太了解 Transformer 为什么是并行训练，请仔细回顾 Transformer 论文中有关自回归机制的描述。

广义自回归模型

除了双向注意力外，作者还将一些掩码生成模型的设计融合进标准自回归模型。这种广义上的自回归模型效果更好，且能缓解双向注意力导致的推理速度慢的问题。

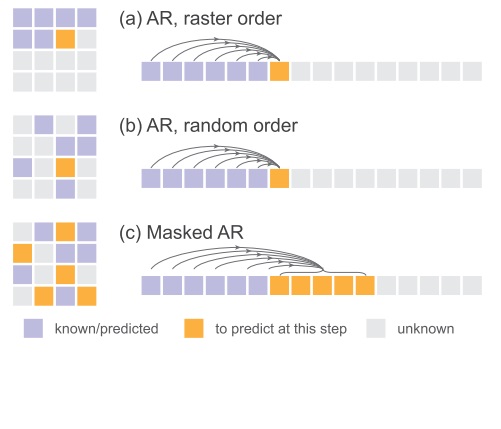
一般来说，用图像自回归模型时，我们都是按从左到右，从上到下的顺序生成词元，如下图 (a) 所示。但是，这种顺序不一定是最合理的。

按理来说，模型应该可以通过任何顺序生成词元，这样模型学到的生成方式更加多样。更合理的生成方式应该如下图 (b) 所示，不是从左到右，从上到下给词元编号，而是随机选择一个排列给图像编号。这样就能按照随机的顺序生成图像的词元了。

而在掩码自回归生成中，模型可以一次性生成任意一个集合的词元。因此，为了加速 (b) 模型，我们可以如下图 (c) 所示，在随机给词元编号后一次生成多个词元。(b) 可以看成是 (c) 一次只预测下一个词元的特例。

Transformer 模型配置

本工作并没有给 Transformer 加入新设计，我们来确认一遍论文中介绍的 Transformer 配置。

本工作依然采取了两阶段的生成方法。第一个阶段的自编码器（又可以理解成 NLP 中的 tokenizer）来自 LDM 工作官方仓库的 VQ-16 和 KL-16 模型。前者是 VQ 自编码器（VQGAN），后者是一个加强版的 VAE。

本工作用的 Transformer 和 ViT 一样。得到图像词元后，词元会加上位置编码，且词元序列开头会附加一个 [cls] 词元，用以在类别约束生成任务里输入类别。

基于这个类别词元，本工作使用了一种特别的 Classifier-free guidance (CFG) 机制：模型用一个假类别词元来表示「类别不明」。训练时，10% 的正确类别词元被替换成了假类别词元。这样，在用扩散模型时，就可以根据标准 CFG 的做法，用正确类别和假类别实现 CFG。详情请参见论文附录 B。

在训练掩码自回归模型时，70%~100% 的词元是未知的。由于采样序列可能会很短，作者在输入序列前附加了 64 个 [cls] 词元。掩码自回归模型的其他主要设计都与 MAE 相同。

实验结果

本工作面向的是图像生成任务，主要评估 ImageNet 数据集上按类别生成的 FID 和 IS 指标。FID 越低越好，IS 越高越好。这篇工作的实验结果中有许多信息，让我们来仔细看一看这份结果。

Diffusion Loss 与广义自回归模型

论文首先展示了 Diffusion Loss、广义自回归模型这两项主要设计的优越性，如下表所示。由于图像是按类别生成的，可以用 CFG 提升模型的生成效果。为了公平比较，模型使用的 VQ 自编码器和 KL 自编码器都来自 LDM 仓库。

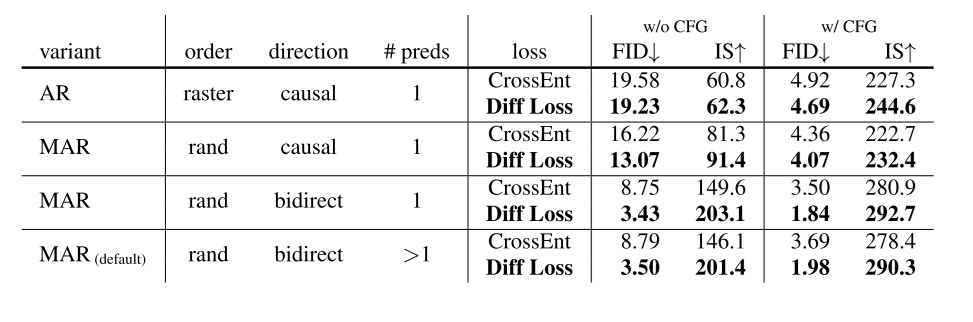
表格的 4 大行展示了改进自回归模型的影响，每一大行里不同 loss 的对比体现了 Diffusioin Loss 的影响。

从第一大行可以看出，Diffusion Loss 似乎对标准自回归的改进不是很明显，且这一套方法的生成能力并不出色。只有把自回归模型逐渐改进后，Diffusion Loss 的效果才能逐渐体现出来。在后几行掩码自回归模型中，Diffusion Loss 的作用还是很大的。

而对比前三大行，我们可以发现自回归模型的架构极大地提升了生成效果，且似乎将 Transformer 由 causal 改成 bidirect 的提升更加显著。

第四大行相比第三大行，提升了每次预测的词元数，主要是为了加速。这两行的对比结果表明，做了这个加速操作后，模型生成能力并没有下降多少。后续实验都是基于第四行的配置。

Diffusion Loss 适配不同的自编码器

相比原来类别分布，用 Diffusion Loss 解除了自编码器必须输出离散图像的限制。因此，目前的模型能够适配多种自编码器，如下表所示。图中 rFID 指的是图像重建任务的 FID，越低越好。这里的 VQ-16 指的是将 VQGAN 的 VQ 层当作解码器的一部分，这样 VQGAN 的编码器输出也可以看成是连续图像，和 LDM 里的做法一样。最后一行的 KL-16 是作者重新重新在 ImageNet 上训练的 VAE，而前两行的 VQ-16 和 KL-16 是在 OpenImages 上训练的。由于后文的实验都基于 ImageNet，所以后文都会用第五行那个 VAE。

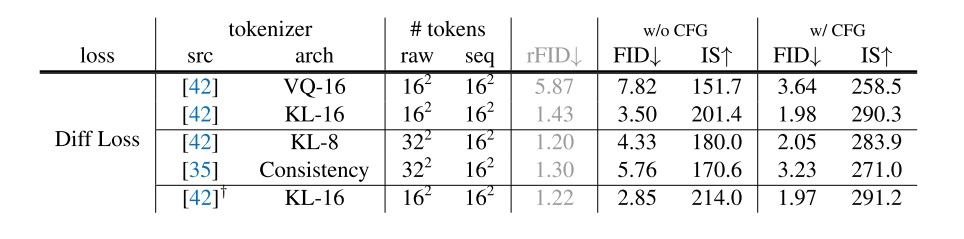
首先对比一下这里 VQ-16 w/o CFG 的 FID 和上表里最后一大行 CrossEnt 的 FID。这两组实验的自编码器相同，仅有误差函数不同。将误差函数从交叉熵换成了 Diffusion Loss 后，FID 从 8.79 变成了 7.82。这一项直接对比的实验证明了不考虑自编码器的改进时，Diffusion Loss 本身的优越性。

再对比前两行，KL 的自编码器无论是图像恢复指标还是最后的生成指标都优于 VQ 的自编码器。这印证了论文开头想要抛弃 VQ 自编码器的动机：VQ 自编码器逊于 KL 自编码器。

第三、第四行展示了方法也可以兼容下采样 8 倍的自编码器。本来测试用的 ImageNet 是 $256 \times 256$ 大小的，按照一开始下采样 16 倍的配置，能得到 $16 \times 16$ 的压缩图像，即输入 Transformer 的词元序列长度为 $16 \times 16$。现在改成了下采样 8 倍后，为了兼容之前 $16 \times 16$ 的序列长度，作者把 $2 \times 2$ 个像素打包成一个词元。论文里没讲是怎么打包的，我猜测是在通道上拼接。Consistency 是另一套自编码器，作者展示这个估计是为了说明这套方法兼容性很强。

和 SOTA 图像生成模型对比

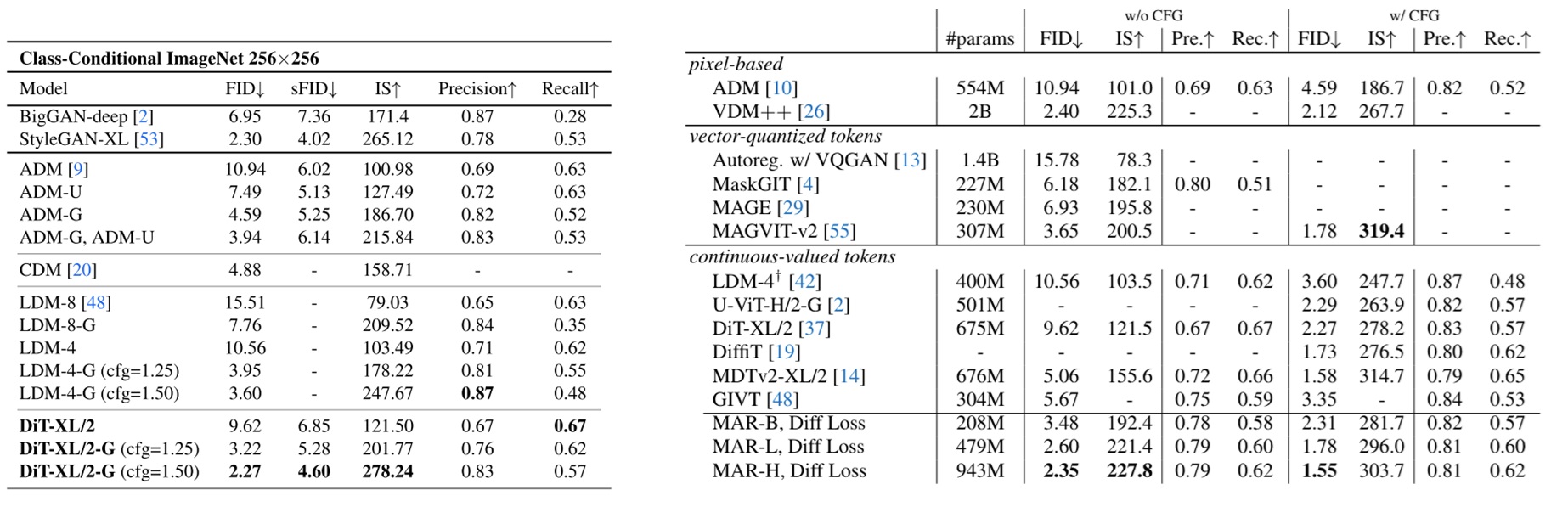
为了证明方法的优越性，论文还展示了本工作与其他 SOTA 工作在 ImageNet 图像生成任务上的定量对比结果。下表是 ImageNet $256 \times 256$ 的结果。为了方便对比，我还贴出了 DiT 论文里展示的表格（左表）。本文的模型在表里被称作 MAR。

下表是 ImageNet $512 \times 512$ 的结果。左边那张表是 EDM2 展示的结果。

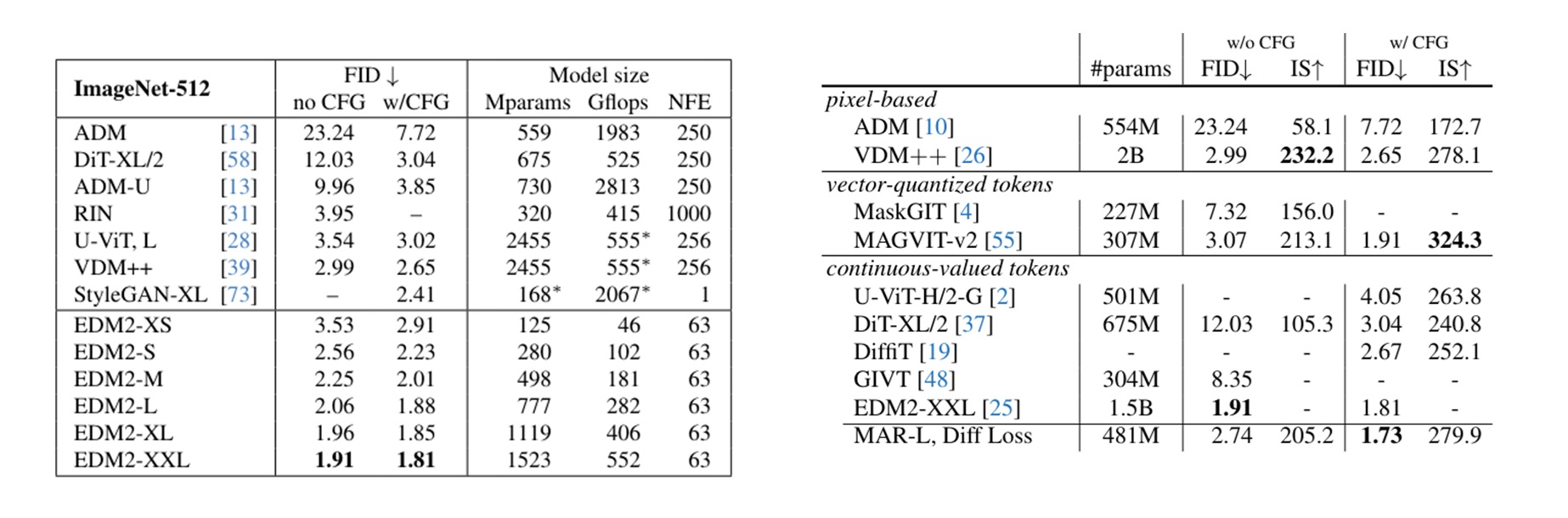
从表里可以看出，本工作在 ImageNet 图像生成任务上表现很不错，超越了绝大多数模型。

图像生成速度对比

下面是不同生成模型的速度对比结果。第一张图是本论文展示的和 DiT 的对比结果。DIT 采用的扩散模型采样步数是 (50 ,75, 150, 250)。由于本工作的性能瓶颈在自回归模型而不在扩散模型上，所以本工作展示的不同采样步数由自回归步数决定。图中的自回归步数是 (8, 16, 32, 64, 128)。中间的图是 LDM 的结果，同模型不同点表示的是采样步数为 (10, 20, 50, 100, 200) 的结果。右边的表是 EDM2 的采样速度等指标。左边两张图是 ImageNet $256 \times 256$ 上的，最右边的表是 ImageNet $512 \times 512$ 上的。

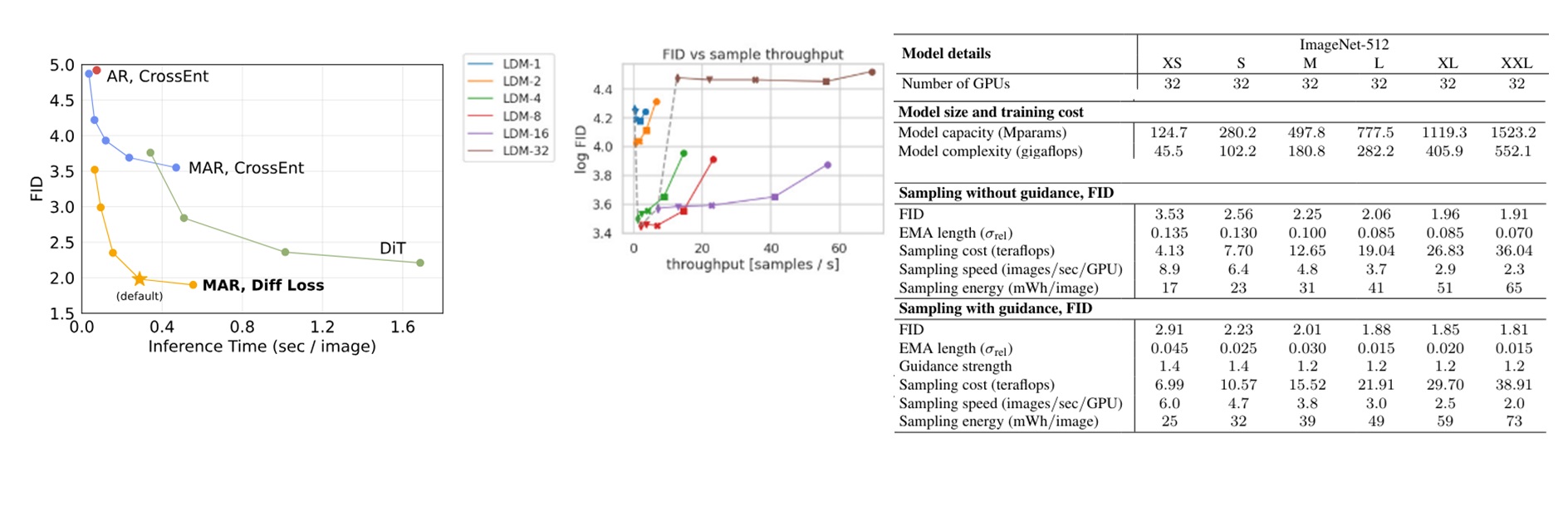
由于不同图表的采样速度指标不太一样，我们将指标统一成每秒生成的图像。从第一张图的对比可以看出，DiT 最快也是一秒 2.5 张图像左右，而 MAR 又快又好，默认（自回归步数 64）一秒生成 3 张图左右。同时，通过 MAR 和有 kv cache 加速的标准 AR 的对比，我们能发现 MAR 在默认自回归步数下还是比标准 AR 慢了不少。

我们再看中间 LDM 的速度。我们观察一下最常使用的 LDM-8。如果是令 DDIM 步数为 20 （第二快的结果）的话，LDM-8 的生成速度在一秒 16 张图像左右，还是比 MAR 快很多。DDIM 步数取 50 时也会比 MAR 快一些。

最后看右边较新的图像扩散模型 EDM2 的速度。由于这个是在 $512 \times 512$ 的图片上测试的，和前面的速度相比时大概要乘个 4。哪怕是最大的 XXL 模型，在有 guidance 时，生成速度也是 2 张图片每秒。换算到 $256 \times 256$ 上约 8 张图片每秒，还是比 MAR 快。

总结

自回归图像生成中的向量离散化和类别分布必须同时使用。为了去除表现较差的向量离散化操作，本工作的作者重新用扩散模型建模了自回归中下一个图像词元的分布，从而提升了模型的生成能力。由于标准自回归模型生成能力有限，为了进一步提升模型，作者又引入了最新的掩码自回归模型。最终的模型在 ImageNet 图像生成指标上取得了几乎最顶尖的结果。

以上是论文的叙述逻辑。但掩码自回归那一块应该是之前工作的研究成果，这篇文章实际上就是把新提出的 diffusion loss 用到了掩码自回归上，把本来在 ImageNet 上生成能力尚可的掩码自回归推到了最前列。

这篇文章在科研上的最大创新是打破了大家在图像自回归上的固有思维，认为必须用离散词元，必须用类别分布。但仔细一想，建模一个分布的方法其实许许多多。随便把另一种生成完整图像的模型用到生成一个像素上，就能取代之前的类别分布，得到更好的图像生成结果。这篇文章用简单的 DDPM 只是为了验证这个想法的可行性，用更复杂的模型或许能有更好的结果，但用 DDPM 做验证就足够了。之后肯定会有各种后续工作，研究如何用更好的模型来建模本框架中一个像素值的分布。

反过来想，这篇文章也在提醒我们，扩散模型并不只是可以用来生成图像，它的本质是建模一个分布。如果某个模型中间需要建模一个简单的分布的话，都可以尝试用 DDPM。

相比其科研创新，这篇文章在 ImageNet 图像生成指标的成就反而没有那么耀眼了。本工作在 ImageNet 的 FID 等指标上取得了几乎最优的结果，战胜了多数最强的扩散模型，有望将大家的科研眼光从扩散模型移到自回归上。但由于自回归本身步数较多，且每一步要在 Transformer 里做完整的注意力操作，这种方法的速度还是比扩散模型要慢一点。

目前 GitHub 上已有本工作的复现：https://github.com/lucidrains/autoregressive-diffusion-pytorch 。