位置编码背后的理论解释——傅里叶特征 (Fourier Feature）与核回归

最近我在看位置编码最新技术时，看到了一个叫做 “NTK-aware” 的词。我想：「”NTK”是什么？Next ToKen （下一个词元）吗？为什么要用这么时髦的缩写？」看着看着，我才发现不对劲。原来，NTK 是神经网络理论里的一个概念，它从 kernel regression 的角度解释了神经网络的学习方法。基于 NTK 理论，有人解释了位置编码的理论原理并将其归纳为一种特殊的 Fourier Feature （傅里叶特征）。这么多专有名词一下就把我绕晕了，我花了几天才把它们之间的关系搞懂。

在这篇文章里，我主要基于论文 Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains （后文简称为「傅里叶特征论文」），介绍傅里叶特征这一概念。为了讲清这些理论的发展脉络，我会稍微讲一下 NTK 等理论概念。介绍完傅里叶特征后，我还会讲解它在其他方法中的应用。希望读完本文后，读者能够以这篇论文为基点，建立一个有关位置编码原理的知识网络，以从更深的层次来思考新的科研方向。

用 MLP 表示连续数据

我们先从一个具体的任务入手，直观体会傅里叶特征能够做些什么事。

我们知道，神经网络，哪怕是最简单的多层感知机（MLP），都有着很强的泛化能力：训练完毕后，对于训练集里完全没见过的输入，网络也能给出很正确的输出。特别地，如果新输入恰好和训练集的某个输入很近，那么它的输出也会和对应的训练集输出很近；随着新输出与训练集输入的距离不断增加，新输出也会逐渐变得不同。这反映了神经网络的连续性：如果输入的变化是连续的，那么输出的变化也是连续的。

基于神经网络的这一特性，有人想到：我们能不能用神经网络来表示连续数据呢？比如我想表达一张处处连续的图像，于是我令神经网络的输入是 (x, y) 表示的二维坐标，输出是 RGB 颜色。之后，我在单张图像上过拟合这个 MLP。这样，学会表示这张图像后，哪怕输入坐标是分数而不是整数，神经网络也能给出一个颜色输出。

这种连续数据有什么好处呢？我们知道，计算机都是以离散的形式来存储数据的。比如，我们会把图像拆成一个个像素，每个像素存在一块内存里。对于图像这种二维数据，计算机的存储空间还勉强够用。而如果想用密集的离散数据表达更复杂的数据，比如 3D 物体，计算机的容量就捉襟见肘了。但如果用一个 MLP 来表达 3D 物体的话，我们只需要存储 MLP 的参数，就能获取 3D 物体在任何位置的信息了。

这就是经典工作神经辐射场 (Neural Radiance Field, NeRF) 的设计初衷。NeRF 用一个 MLP 拟合 3D 物体的属性，其输入输出如下图所示。我们可以用 MLP 学习每个 3D 坐标的每个 2D 视角处的属性（这篇文章用的属性是颜色和密度）。根据这些信息，利用某些渲染算法，我们就能重建完整的 3D 物体。

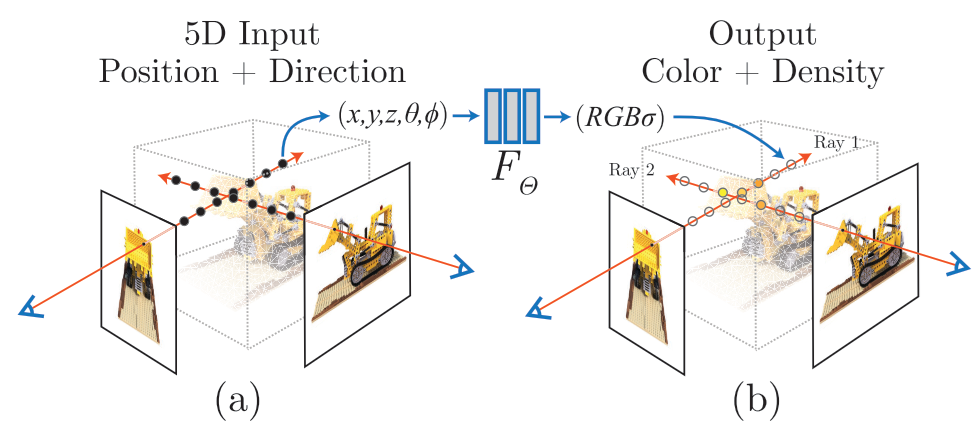
上述过程看起来好像很简单直接。但在 NeRF 中，有一个重要的实现细节：必须给输入加上位置编码，MLP 才能很好地过拟合连续数据。这是为什么呢？让我们先用实验复现一下这个现象。

MLP 拟合连续图像实验

为了快速复现和位置编码相关的问题，我们简单地用一个 MLP 来表示图像：MLP 的输入是 2D 坐标，输出是此处的三通道 RGB 颜色。我为这篇博文创建一个 GitHub 文件夹 https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/FourierFeature ，该实验的 Notebook 代码在文件夹的 image_mlp.ipynb 中，欢迎大家 clone 项目并动手尝试。

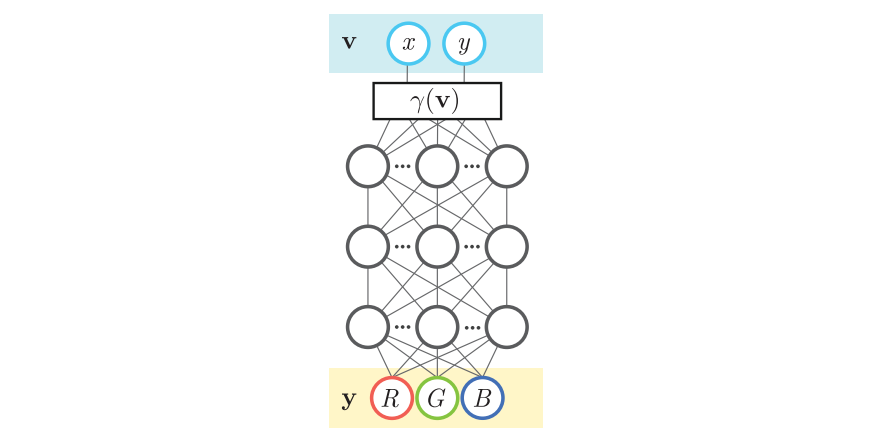
一开始，我们先导入库并可视化要拟合的图片。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision.io import read_image, ImageReadMode
from torchvision.transforms.functional import to_pil_image

from tqdm import tqdm
from einops import rearrange

def viz_image(pt_img: torch.Tensor):
    pil_img = to_pil_image(pt_img)
    display(pil_img)

    
input_image = read_image('misuzu.png', ImageReadMode.RGB)
input_image = input_image.to(torch.float32) / 255
input_image = input_image.unsqueeze(0)
input_image = F.interpolate(input_image, (256, 256), mode='bilinear')
viz_image(input_image[0])

我们再定义一个 MLP 类。稍后我们会并行地传入二维坐标。具体来说，我们会将输入定义为一个 [1, 2, H, W] 形状的数据，其中通道数 2 表示 (i, j) 格式的坐标。由于输入是以图像的形式并行输入的，我们可以用 $1 \times 1$ 的 2D 卷积来表示二维数据上的并行 MLP。所以在下面这个 MLP 里，我们只用到 $1 \times 1$ 卷积、激活函数、归一化三种层。按照傅里叶特征论文的官方示例，网络最后要用一个 Sigmoid 激活函数调整输出的范围。

class MLP(nn.Module):
    def __init__(self, in_c, out_c=3, hiden_states=256):
        super().__init__()
        self.mlp = nn.Sequential(
            nn.Conv2d(in_c, hiden_states, 1), nn.ReLU(), nn.BatchNorm2d(hiden_states),
            nn.Conv2d(hiden_states, hiden_states, 1), nn.ReLU(), nn.BatchNorm2d(hiden_states),
            nn.Conv2d(hiden_states, hiden_states, 1), nn.ReLU(), nn.BatchNorm2d(hiden_states),
            nn.Conv2d(hiden_states, out_c, 1), nn.Sigmoid()
        )

    def forward(self, x):
        return self.mlp(x)

之后我们来定义训练数据。在一般的任务中，输入输出都是从训练集获取的。而在这个任务中，输入是二维坐标，输出是图像的颜色值。输出图像 input_image 我们刚刚已经读取完毕了，现在只需要构建输入坐标即可。我们可以用下面的代码构建一个 [1, 2, H, W] 形状的二维网格，grid[0, :, i, j] 处的数据是其坐标 (i, j) 本身。当然，由于神经网络的输入一般要做归一化，所以我们会把原本 0~H 和 0~W 里的高宽坐标缩放都到 0~1。最终 grid[0, :, i, j]==(i/H, j/W)。

H, W = input_image.shape[2:]

h_coord = torch.linspace(0, 1, H)
w_coord = torch.linspace(0, 1, W)
grid = torch.stack(torch.meshgrid([h_coord, w_coord]), -1).permute(2, 0, 1).unsqueeze(0)

准备好一切后，我们就可以开始训练了。我们初始化模型 model 和优化器 optimizer，和往常一样训练这个 MLP。如前所述，这个任务的输入输出非常直接，输入就是坐标网格 grid，目标输出就是图片 input_image。每训练一段时间，我们就把当前 MLP 拟合出的图片和误差打印出来。

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

model = MLP(2).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-4)
n_loops = 400
input_image = input_image.to(device)
grid = grid.to(device)
for epoch in tqdm(range(n_loops)):
    output = model(grid)
    loss = F.l1_loss(output, input_image)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch % 100 == 0 or epoch == n_loops - 1:
        viz_image(output[0])
        print(loss.item())

运行代码，大致能得到如下输出。可以看到，从一开始，图像就非常模糊。

不过，如果我们在把坐标输入进网络前先将其转换成位置编码——一种特殊的傅里叶特征，那么 MLP 就能清晰地拟合出原图片。这里我们暂时不去关注这段代码的实现细节。

class FourierFeature(nn.Module):
    def __init__(self, in_c, out_c, scale):
        super().__init__()
        fourier_basis = torch.randn(in_c, out_c // 2) * scale
        self.register_buffer('_fourier_basis', fourier_basis)
        
    def forward(self, x):
        N, C, H, W = x.shape
        x = rearrange(x, 'n c h w -> (n h w) c')
        x = x @ self._fourier_basis
        x = rearrange(x, '(n h w) c -> n c h w', h = H, w = W)
            
        x = 2 * torch.pi * x
        x = torch.cat([torch.sin(x), torch.cos(x)], dim=1) 
        return x
        
feature_length = 256
model = MLP(feature_length).to(device)
fourier_feature = FourierFeature(2, feature_length, 10).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-4)
n_loops = 400
for epoch in tqdm(range(n_loops)):
    x = fourier_feature(grid)
    output = model(x)
    loss = F.l1_loss(output, input_image)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch % 100 == 0 or epoch == n_loops - 1:
        viz_image(output[0])
        print(loss.item())
prev_output = output

简单地对比一下，此前方法的主要问题是 MLP 无法拟合高频的信息（如图块边缘），只能生成模糊的图像。而使用位置编码后，MLP 从一开始就能较好地表示高频信息。可见，问题的关键在于如何让 MLP 更好地拟合数据的高频信息。

接下来，我们来从一个比较偏理论的角度看一看论文是怎么分析位置编码在拟合高频信息中的作用的。

核回归

傅里叶特征论文使用了神经正切核（Nerual Tangent Kernel, NTK）来分析 MLP 的学习规律，而 NTK 又是一种特殊的核回归 (Kernel Regression) 方法。在这一节里，我会通过代码来较为仔细地介绍核回归。下一节我会简单介绍 NTK。

和神经网络类似，核回归也是一种数学模型。给定训练集里的输入和输出，我们建立这样一个模型，用来拟合训练集表示的未知函数。相比之下，核回归的形式更加简单，我们有更多的数学工具来分析其性质。

核回归的设计思想来源于我们对于待拟合函数性质的观察：正如我们在前文的分析一样，要用模型拟合一个函数时，该模型在训练数据附近最好是连续变化的。离训练集输入越近，输出就要和其对应输出越近。基于这种想法，核回归直接利用和所有数据的相似度来建立模型：假设训练数据为 $(x_i, y_i), i \in [1, n]$，我们定义了一个计算两个输入相似度指标 $K(x_1, x_2)$，那么任意输入 $x$ 的输出为：

$$w_i = \frac{K(x_i, x)}{\sum_{i=1}^{n}K(x_i, x)} \\ f(x) = \sum_{i=1}^{n}w_iy_i$$

也就是说，对于一个新输入 $x$，我们算它和所有输入 $x_i$ 的相似度 $w_i$，并把相似度归一化。最后的输出 $f(x)$ 是现有 $y_i$ 的相似度加权和。

这样看来，只要有了相似度指标，最终模型的形式也就决定下来了。我们把这个相似度指标称为「核」。至于为什么要把它叫做核，是因为这个相似度指标必须满足一些性质，比如非负、对称。但我们这里不用管那么多，只需要知道核是一种衡量距离的指标，决定了核就决定了核回归的形式。

我们来通过一个简单的一维函数拟合实验来进一步熟悉核回归。该实验代码在项目文件夹下的 kernel_regression.ipynb 中。

先导入库。

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

再创建一个简单的非线性函数，做为我们的拟合目标。这个函数就是一个简单的周期为 $2$ 的正弦函数乘上线性函数 $(1-x)$。我们可以简单可视化一下函数在 $[-1, 1]$ 之间的图像。

def func(x):
    return np.sin(np.pi * x) * (1 - x)

xs = np.linspace(-1, 1, 100)
ys = func(xs)
plt.plot(xs, ys)
plt.show()

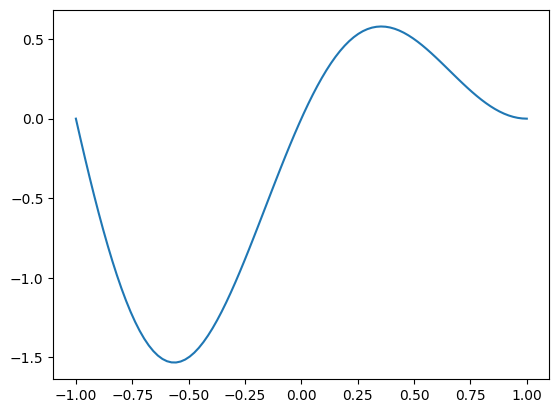
基于这个函数，我们等间距地选一些点做为训练数据。

sample_x = np.linspace(-1, 1, 10)
sample_y = func(sample_x)
plt.scatter(sample_x, sample_y)
plt.show()

有了数据后，我们来用核回归根据数据拟合这个函数。在决定核回归时，最重要的是决定核的形式。这里我们用正态分布的概率密度函数来表示核，该核唯一的超参数是标准差，需要我们根据拟合结果手动调整。标准差为 1 的标准正态分布核的图像如下所示。由于最后要做归一化，正态分布密度函数的系数被省略掉了。

def kernel_func(x_ref, x_input, sigma=1):
    return np.exp(-(x_input-x_ref)**2 / (2 * sigma**2))

xs = np.linspace(-1, 1, 100)
ys = kernel_func(0, xs)
plt.plot(xs, ys)
plt.show()

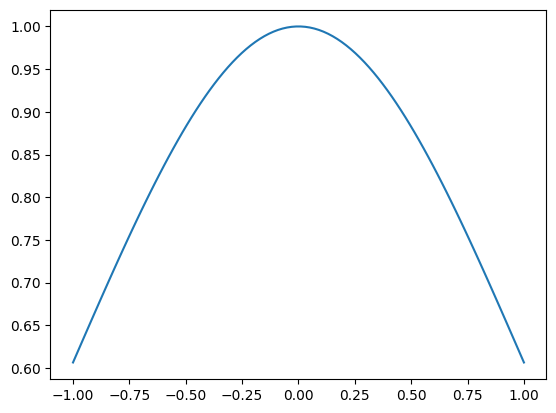
可以从图像中看出，离某输入越近（假设该输入是 0），那么相似度就越高。这符合我们对于相似度函数的要求。

有了核函数后，我们就直接得到了模型。根据核回归模型计算结果的函数为 kernel_regression。函数参数 xs, ys 表示训练数据，x_input 表示测试时用的输入坐标，sigma 是核回归的超参数。

假设有 n 个训练样本，有 m 个测试输入，那么我们要计算每个测试输入对每个训练输入的 n * m 个相似度，这些相似度会存到矩阵 weight 里。为此，我们需要对 xs 和 x_input 做一些形状变换，再用上面定义的核函数 kernel_func 求出每对相似度。有了相似度后，我们根据公式计算点乘结果 weight_dot 及归一化系数 weight_sum，并最终计算出核回归的结果 res。

基于这个函数，我们可以将测试输入定义成 [-1, 1] 上一些更密集的坐标，并用上面定义好的 10 个样本做为训练集，得到核回归的结果。

def kernel_regression(xs, ys, x_input, sigma=1):
    # xs: [n, ]
    # ys: [n, ]
    # x_input: [m, ]
    N = xs.shape[0]
    xs = np.expand_dims(xs, 1)
    ys = np.expand_dims(ys, 1)
    x_input = np.expand_dims(x_input, 0)
    x_input = np.repeat(x_input, N, 0)
    weight = kernel_func(xs, x_input, sigma) # [n, m]
    weight_sum = np.sum(weight, 0)
    weight_dot = weight.T @ ys
    weight_dot = np.squeeze(weight_dot, 1)
    res = weight_dot / weight_sum
    return res

sigma = 1
xs = np.linspace(-1, 1, 100)
ys = kernel_regression(sample_x, sample_y, xs, sigma)
plt.title(f'sigma = {sigma}')
plt.plot(xs, ys)
plt.show()

我们可以通过修改 sigma 来得到不同的拟合效果。以下是我的一些结果：

可以看出，标准差越小，模型倾向于过拟合；随着标准差变大，曲线会逐渐平缓。我们需要不断调整超参数，在过拟合和欠拟合之间找到一个平衡。这种现象很容易解释：正态分布核函数的标准差越小，意味着每个训练数据的影响范围较小，那么测试样本更容易受到少数样本的影响；标准差增大之后，各个训练样本的影响开始共同起作用，我们拟合出的函数也越来越靠近正确的函数；但如果标准差过大，每个训练样本的影响都差不多，那么模型就什么都拟合不了了。

从实验结果中，我们能大致感受到核回归和低通滤波很像，都是将已知数据的平均效果施加在未知数据上。因此，在分析核回归的时候，往往会从频域分析核函数。如果核函数所代表低通滤波器的带宽 （bandwidth）越大，那么剩下的高频信息就更多，核回归也更容易拟合高频信息较多的数据。

神经正切核

那么，核回归是怎么和神经网络关联起来的呢？有研究表明，在一些特殊条件下，MLP 的最终优化结果可以用一个简单的核回归来表示。这不仅意味着我们可以神奇地提前预测梯度下降的结果，还可以根据核回归的性质来分析神经网络的部分原理。这种能表示神经网络学习结果的核被称为神经正切核（NTK）。

这些特殊条件包括 MLP 无限宽、SGD 学习率的学习率趋近 0 等。由于这些条件和实际神经网络的配置相差较远，我们难以直接用核回归预测复杂神经网络的结果。不过，我们依然可以基于这些理论来分析和神经网络相关的问题。傅里叶特征的分析就是建立在 NTK 上的。

NTK 的形式为

$$k_{NTK}(\mathbf{x_i}, \mathbf{x_j}) = \mathbb{E}_{\theta\sim\mathcal{N}} \langle\frac{\partial f(\mathbf{x_i}; \theta)}{\partial \theta}, \frac{\partial f(\mathbf{x_j}; \theta)}{\partial \theta} \rangle，$$

其中，$f$ 是参数为 $\theta$ 的神经网络，$\langle\cdot,\cdot \rangle$为内积运算。简单来看，这个式子是说神经网络的核回归中，任意两个向量间的相似度等于网络对参数的偏导的内积的期望。基于 NTK，我们可以分析出很多神经网络的性质，比如出乎意料地，神经网络的结果和随机初始化的参数无关，仅和网络结构和训练数据有关。

在学习傅里叶特征时，我们不需要仔细研究这些这些理论，而只需要知道一个结论：一般上述 NTK 可以写成标量函数 $h_{NTK}(\mathbf{x}_i^T\mathbf{x}_j)$，也就是可以先算内积再求偏导。这意味用核回归表示神经网络时，真正要关心的是输入间的内积。别看 NTK 看起来那么复杂，傅里叶特征论文其实主要就用到了这一个性质。

为了从理论上讲清为什么 MLP 难以拟合高频，作者还提及了很多有关 NTK 的分析，包括一种叫做谱偏差（spectral bias）的现象：神经网络更容易学习到数据中的低频特征。可能作者默认读者已经熟悉了相关的理论背景，这部分论述经常会出现逻辑跳跃，很难读懂。当然，不懂这些理论不影响理解傅里叶特征。我建议不要去仔细阅读这篇文章有关谱偏差的那一部分。

正如我们在前文的核回归实验里观察到的，核回归模型能否学到高频取决于核函数的频域特征。因此，这部分分析和 NTK 的频域有关。对这部分内容感兴趣的话可以去阅读之前有关谱偏差的论文。

傅里叶特征的平移不变性

在上两节中，我们花了不少功夫去认识谱回归和 NTK。总结下来，其实我们只需要搞懂两件事：

• 神经网络最终的收敛效果可以由简单的核回归决定。而核回归重点是定义两个输入之间的相似度指标（核函数）。
• 表示神经网络的核回归相似度指标是 NTK，它其实又只取决于两个输入的内积 $\mathbf{x}_i^T\mathbf{x}_j$。

根据这一性质，我们可以部分解释为什么在文章开头那个 MLP 拟合连续图像的实验中，位置编码可以提升 MLP 拟合高频信息的能力了。这和位置输入的特性有关。

当 MLP 的输入表示位置时，我们希望模型对输入位置具有平移不变性。比如我们现在有一条三个样本组成的句子 $(1, A), (2, B), (3, C)$。当我们同时改变句子的位置信息时，比如将句子的位置改成 $(11, A), (12, B), (13, C)$时，网络能学出完全一样的东西。但显然不对输入位置做任何处理的话， $(1, 2, 3)$ 和 $(11, 12, 13)$ 对神经网络来说是完全不同的意思。

而使用位置编码的话，情况就完全不同了。假如输入数据是二维坐标 $\mathbf{v}\in [0, 1)^d$，我们可以用下面的式子建立一个维度为 $2m$ 的位置编码：

其中 $a_i$ 是系数， $b \in \mathbb{R}^{m \times 2}$ 是一个投影矩阵，用于把原来 2D 的位置变成一个更长的位置编码。当然，由于位置编码中既要有 $\sin$ 也要有 $\cos$，所以最终的位置编码长度为 $2m$。

根据我们之前的分析，NTK 只取决于输入间的内积。算上位置编码后，一对输入位置 $\mathbf{v}_1, \mathbf{v}_2$ 的内积为：

$$\gamma(\mathbf{v_1})^T\gamma(\mathbf{v_2}) = [a_1^2 \cos(2\pi \mathbf{b_1}^T\mathbf{v_1})\cos(2\pi \mathbf{b_1}^T\mathbf{v_2})+a_1^2 \sin(2\pi \mathbf{b_1}^T\mathbf{v_1})\sin(2\pi \mathbf{b_1}^T\mathbf{v_2}) + ...]$$

而根据三角函数和角公式可知：

$$\cos(\alpha-\beta)=\cos\alpha \cos\beta + \sin\alpha \sin\beta$$

这样，上面那个内积恰好可以写成：

$$\gamma(\mathbf{v_1})^T\gamma(\mathbf{v_2}) = [a_1^2\cos(2\pi \mathbf{b_1}^T (\mathbf{v_1}-\mathbf{v_2})) + ...]$$

上式完全由位置间的相对距离 $\mathbf{v_1}-\mathbf{v_2}$ 决定。上式决定了 NTK，NTK 又决定了神经网络的学习结果。所以，神经网络的收敛结果其实完全取决于输入间的相对距离，而不取决于它们的绝对距离。也因此，位置编码使得 MLP 对于输入位置有了平移不变性。

加入位置编码后，虽然 MLP 满足了平移不变性，但这并不代表 MLP 学习高频信息的能力就变强了。平移不变性能给我们带来什么好处呢？作者指出，当满足了平移不变性后，我们就能手动调整 NTK 的带宽了。回想一下我们上面做的核回归实验，如果我们能够调整核的带宽，就能决定函数是更加高频（尖锐）还是更加低频（平滑）。这里也是同理，如果我们能够调大 NTK 的带宽，让它保留更多高频信息，那么 MLP 也就能学到更多的高频信息。

作者在此处用信号处理的知识来分析平移不变性的好处，比如讲了新的 NTK 就像一个重建卷积核 （reconstruction filter），整个 MLP 就像是在做卷积。还是由于作者省略了很多推导细节，这部分逻辑很难读懂。我建议大家直接记住推理的结论：平移不变性使得我们能够调整 NTK 的带宽，从而调整 MLP 学习高频的能力。

那我们该怎么调整 NTK 的带宽呢？现在的新 NTK 由下面的式子决定：

$$\gamma(\mathbf{v_1})^T\gamma(\mathbf{v_2}) = \sum_{j=1}^m a_j^2\cos(2\pi \mathbf{b_j}^T (\mathbf{v_1}-\mathbf{v_2}))$$

为了方便分析，我们假设$\mathbf{v}$和$\mathbf{b_j}$都是一维实数。那么，如果我们令$b_j=j$的话：

$$\gamma(\mathbf{v_1})^T\gamma(\mathbf{v_2}) = \sum_{j=1}^m a_j^2\cos(2\pi j (\mathbf{v_1}-\mathbf{v_2}))$$

这个式子能令你想到什么？没错，就是傅里叶变换。$j$ 较大的项就表示 NTK 的高频分量。我们可以通过修改前面的系数 $a_j$ 来手动调整 NTK 的频域特征。我们能看到，位置编码其实就是在模拟傅里叶变换，所以作者把位置编码总结为傅里叶特征。

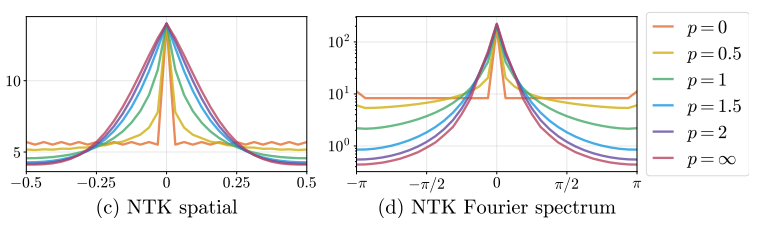
作者通过实验证明我们可以手动修改 NTK 的频谱。实验中，作者令 $b_j=j, a_j=1/j^p$。$p=\infty$ 表示位置编码只有第一项：$\gamma(v)=[\cos 2\pi v, \sin 2\pi v]^T$。不同 $p$ 时 NTK 的空域和频域示意图如下所示。可以看出，令 $p=0$ 时，即傅里叶特征所有项的系数都为 $1$ 时，NTK 的高频分量不会衰减。这也意味着 MLP 学高频信息和低频信息的能力差不多。

随机傅里叶特征

现在我们已经知道傅里叶特征的公式是什么，并知道如何设置其中的参数 $a_j$, $\mathbf{b}_j$ 了。现在，还有一件事我们没有决定：该如何设置傅里叶特征的长度 $m$ 呢？

既然我们说傅里叶特征就是把输入的位置做了一次傅里叶变换，那么一般来讲，傅里叶特征的长度应该和原图像的像素数一样。比如我们要表示一个 $256 \times 256$ 的图像，那么我们就需要令 $m = 256 \times 256 / 2$ ，$\mathbf{b}$ 表示不同方向上的频率：$[(1, 1), (1, 2), …, (128, 256)]$。但这样的话，神经网络的参数就太多了。可不可以令 $m$ 更小一点呢？

根据之前的研究 Random features for large-scale kernel machines 表明，我们不需要密集地采样傅里叶特征，只需要稀疏地采样就行了。具体来说，我们可以从某个分布随机采样 $m$ 个频率 $\mathbf{b_j}$ 来，这样的学习结果和密集采样差不多。当然，根据前面的分析，我们还是令所有系数 $a_j=1$。在实验中，作者发现，$\mathbf{b_j}$ 从哪种分布里采样都无所谓，关键是 $\mathbf{b_j}$ 的采样分布的标准差，因为这个标准差决定了傅里叶特征的带宽，也决定了网络拟合高频信息的能力。实验的结果如下：

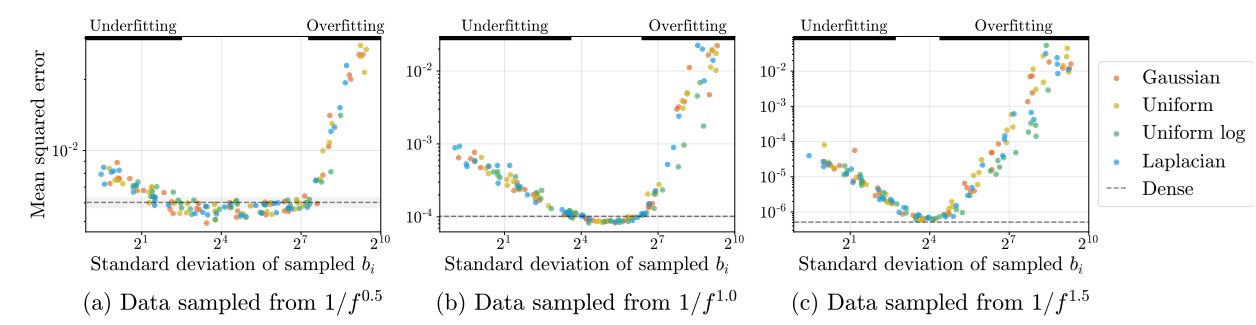
我们可以不管图片里 $1/f^x$ 是啥意思，只需要知道 a, b, c 是三组不同的实验就行。虚线是密集采样傅里叶特征的误差，它的结果反映了一个「较好」的误差值。令人惊讶的是，不管从哪种分布里采样 $\mathbf{b_j}$，最后学出来的网络误差都差不多。问题的关键在于采样分布的标准差。把标准差调得够好的话，模型的误差甚至低于密集采样的误差。

也就是说，虽然我们花半天分析了位置编码和傅里叶变换的关系，但我们没必要照着傅里叶变换那样密集地采样频率，只需要随机选一些频率即可。当然，这个结论只对 MLP 拟合连续数据的任务有效，和 Transformer 里的位置编码无关。

代码实现随机傅里叶特征

现在，我们可以回到博文开头的代码，看一下随机傅里叶特征是怎么实现的。

class FourierFeature(nn.Module):
    def __init__(self, in_c, out_c, scale):
        super().__init__()
        fourier_basis = torch.randn(in_c, out_c // 2) * scale
        self.register_buffer('_fourier_basis', fourier_basis)
        
    def forward(self, x):
        N, C, H, W = x.shape
        x = rearrange(x, 'n c h w -> (n h w) c')
        x = x @ self._fourier_basis
        x = rearrange(x, '(n h w) c -> n c h w', h = H, w = W)
            
        x = 2 * torch.pi * x
        x = torch.cat([torch.sin(x), torch.cos(x)], dim=1) 
        return x
        
feature_length = 256
model = MLP(feature_length).to(device)
fourier_feature = FourierFeature(2, feature_length, 10).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-4)
n_loops = 400
for epoch in tqdm(range(n_loops)):
    x = fourier_feature(grid)
    output = model(x)
    loss = F.l1_loss(output, input_image)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch % 100 == 0 or epoch == n_loops - 1:
        viz_image(output[0])
        print(loss.item())
prev_output = output

傅里叶特征通过类 FourierFeature 实现。其代码如下：

class FourierFeature(nn.Module):
    def __init__(self, in_c, out_c, scale):
        super().__init__()
        fourier_basis = torch.randn(in_c, out_c // 2) * scale
        self.register_buffer('_fourier_basis', fourier_basis)
        
    def forward(self, x):
        N, C, H, W = x.shape
        x = rearrange(x, 'n c h w -> (n h w) c')
        x = x @ self._fourier_basis
        x = rearrange(x, '(n h w) c -> n c h w', h = H, w = W)
            
        x = 2 * torch.pi * x
        x = torch.cat([torch.sin(x), torch.cos(x)], dim=1) 
        return x

构造函数里的 fourier_basis 表示随机傅里叶特征的频率，对应论文公式里的$\mathbf{b}$，scale 表示采样的标准差。初始化好了随机频率后，对于输入位置 x，只要按照公式将其投影到长度为 out_c / 2 的向量上，再对向量的每一个分量求 sin, cos 即可。按照之前的分析，我们令所有系数 $a$ 为 $1$，所以不需要对输出向量乘系数。

傅里叶特征在 StyleGAN3 里的应用

傅里叶特征最经典的应用就是 NeRF 这类过拟合连续数据任务。除此之外，傅里叶特征另一次大展身手是在 StyleGAN3 中。

StyleGAN3 希望通过平滑地移动生成网络的输入来使输出图片也发生对应的移动。为此，StyleGAN3 将生成网络的输入定义为频域上的一个有限带宽图像信号：根据信号处理知识，我们能够将有限带宽信号转换成空域上无限连续的信号。也就是说，不管输入的分辨率（采样率）多低，我们都能够平滑地移动输入图片。StyleGAN3 借助随机傅里叶特征来实现这样一个频域图像。

以下代码选自 StyleGAN3 中傅里叶特征的构造函数。这个函数的关键是随机生成一些频率固定，但方向可以不同的傅里叶频率。函数先随机采样了一些频率，再将它们归一化，最后乘上指定的带宽 bandwidth，保证所有频率大小相等。

class SynthesisInput(torch.nn.Module):
    def __init__(self,
        w_dim,          # Intermediate latent (W) dimensionality.
        channels,       # Number of output channels.
        size,           # Output spatial size: int or [width, height].
        sampling_rate,  # Output sampling rate.
        bandwidth,      # Output bandwidth.
    ):
        super().__init__()
        self.w_dim = w_dim
        self.channels = channels
        self.size = np.broadcast_to(np.asarray(size), [2])
        self.sampling_rate = sampling_rate
        self.bandwidth = bandwidth

        # Draw random frequencies from uniform 2D disc.
        freqs = torch.randn([self.channels, 2])
        radii = freqs.square().sum(dim=1, keepdim=True).sqrt()
        freqs /= radii * radii.square().exp().pow(0.25)
        freqs *= bandwidth
        phases = torch.rand([self.channels]) - 0.5

而在使用这个类获取网络输入时，和刚刚的 MLP 实现一样，我们会先生成一个二维坐标表格 grid 用于查询连续图片每一处的颜色值，再将其投影到各个频率上，并计算新向量的正弦函数。

这段代码中，有两块和我们自己的实现不太一样。第一，StyleGAN3 允许对输入坐标做仿射变换（平移和旋转）。仿射变换对坐标的影响最终会转化成对三角函数相位 phases 和频率 freqs 的影响。第二，在计算三角函数时，StyleGAN3 只用了正弦函数，没有用余弦函数。

def forward(self, ...):
   ...

    # Transform frequencies.
    phases = ...
    freqs = ...

    # Construct sampling grid.
    theta = torch.eye(2, 3, device=w.device)
    theta[0, 0] = 0.5 * self.size[0] / self.sampling_rate
    theta[1, 1] = 0.5 * self.size[1] / self.sampling_rate
    grids = torch.nn.functional.affine_grid(theta.unsqueeze(0), [1, 1, self.size[1], self.size[0]], align_corners=False)

    # Compute Fourier features.
    x = (grids.unsqueeze(3) @ freqs.permute(0, 2, 1).unsqueeze(1).unsqueeze(2)).squeeze(3) # [batch, height, width, channel]
    x = x + phases.unsqueeze(1).unsqueeze(2)
    x = torch.sin(x * (np.pi * 2))
    x = x * amplitudes.unsqueeze(1).unsqueeze(2)

    ...

    # Ensure correct shape.
    x = x.permute(0, 3, 1, 2) # [batch, channel, height, width]
    return x

我们在 MLP 拟合连续图像的实验里复现一下这两个改动。首先是二维仿射变换。给定旋转角 theta 和两个方向的平移 tx, ty，我们能够构造出一个 $3 \times 3$ 的仿射变换矩阵。把它乘上坐标 [x, y, 1] 后，就能得到仿射变换的输出。我们对输入坐标 grid 做仿射变换后得到 grid_ext，再用 grid_ext 跑一遍傅里叶特征和 MLP。

N, C, H, W = grid.shape
tx = 50 / H
ty = 0
theta = torch.tensor(torch.pi * 1 / 8)
affine_matrix = torch.tensor([
    [torch.cos(theta), -torch.sin(theta), tx],
    [torch.sin(theta), torch.cos(theta), ty],
    [0, 0, 1]
]
).to(device)
grid_ext = torch.ones(N, 3, H, W).to(device)
grid_ext[:, :2] = grid.clone()
grid_ext = grid_ext.permute(0, 2, 3, 1)
grid_ext = (grid_ext @ affine_matrix.T)
grid_ext = grid_ext.permute(0, 3, 1, 2)[:, :2]

x = fourier_feature(grid_ext)
output = model(x)
viz_image(output[0])

在示例代码中，我们可以得到旋转 45 度并向下平移 50 个像素的图片。可以看到，变换成功了。这体现了连续数据的好处：我们可以在任意位置对数据采样。当然，由于这种连续数据是通过过拟合实现的，在训练集没有覆盖的坐标处无法得到有意义的颜色值。

之后，我们来尝试在傅里叶特征中只用正弦函数。我们将投影矩阵的输出通道数从 out_c / 2 变成 out_c，再在 forward 里只用 sin 而不是同时用 sin, cos。经实验，这样改了后完全不影响重建质量，甚至由于通道数更多了，重建效果更好了。

class FourierFeature(nn.Module):
    def __init__(self, in_c, out_c, scale):
        super().__init__()
        fourier_basis = torch.randn(in_c, out_c) * scale
        self.register_buffer('_fourier_basis', fourier_basis)
        
    def forward(self, x):
        N, C, H, W = x.shape
        x = rearrange(x, 'n c h w -> (n h w) c')
        x = x @ self._fourier_basis
        x = rearrange(x, '(n h w) c -> n c h w', h = H, w = W)
            
        x = 2 * torch.pi * x
        x = torch.sin(x)
        return x

StyleGAN3 论文并没有讲为什么只用 sin，网上也很少有人讨论傅里叶特征的实现细节。我猜傅里叶特征并不是非得和傅里叶变换完全对应，毕竟它只是用来给神经网络提供更多信息，而没有什么严格的意义。只要把输入坐标分解成不同频率后，神经网络就能很好地学习了。

只用 sin 而不是同时用 sin, cos 后，似乎我们之前对 NTK 平移不变的推导完全失效了。但是，根据三角函数的周期性可知，只要是把输入映射到三角函数上后，网络主要是从位置间的相对关系学东西。绝对位置对网络来说没有那么重要，不同的绝对位置只是让所有三角函数差了一个相位而已。只用 sin 的神经网络似乎也对绝对位置不敏感。为了证明这一点，我把原来位于 [0, 1] 间的坐标做了一个幅度为 10 的平移。结果网络的误差几乎没变。

for epoch in tqdm(range(n_loops)):
    x = fourier_feature(grid + 10)
    output = model2(x)
    loss = F.l1_loss(output, input_image)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

根据这些实验结果，我感觉是不是从 NTK 的角度来分析傅里叶特征完全没有必要？是不是只要从直觉上理解傅里叶特征的作用就行了？按我的理解，傅里叶特征在真正意义在于显式把网络对于不同频率的关注度建模出来，从而辅助网络学习高频细节。

总结

在这篇博文中，我们学习了傅里叶特征及其应用，并顺带了解其背后有关核回归、NTK 的有关理论知识。这些知识很杂乱，我来按逻辑顺序把它们整理一下。

为了解释为什么 NeRF 中的位置编码有效，傅里叶特征论文研究了用 MLP 拟合连续数据这一类任务中如何让 MLP 更好地学到高频信息。论文有两大主要结论：

• 通过从 NTK 理论的分析，位置编码其实是一种特殊的傅里叶特征。这种特征具有平移不变性。因此，神经网络就像是在对某个输入信号做卷积。而我们可以通过调整傅里叶特征的参数来调整卷积的带宽，也就是调整网络对于不同频率的关注程度，从而使得网络不会忽略高频信息。
• 傅里叶特征的频率不需要密集采样，只需要从任意一个分布随机稀疏采样。影响效果的关键是采样分布的标准差，它决定了傅里叶特征的带宽，也就决定了网络是否能关注到高频信息。

由于这些结论比较抽象，我们可以通过一个简单的二维图像拟合实验来验证论文的结论。实验表明直接将坐标输入给 MLP 不太行，必须将输入转换成傅里叶特征才能有效让网络学到高频信息。这个傅里叶特征可以是随机、稀疏的。

除了过拟合连续数据外，傅里叶特征的另一个作用是直接表示带宽有限信号，以实现在空域上的连续采样。StyleGAN3 在用傅里叶特征时，允许对输入坐标进行仿射变换，并且计算特征时只用了正弦函数而不是同时用正弦、余弦函数。这表明有关 NTK 的理论分析可能是没有必要的，主要说明问题的还是实验结果。

傅里叶特征论文仅研究了拟合连续数据这一类问题，没有讨论 Transformer 中位置编码的作用。论文中的一些结论可能无法适用。比如在大模型的位置编码中，我们还是得用密集的 sin, cos 变换来表示位置编码。不过，我们可以依然借助该论文中提到的理论分析工具，来尝试分析所有位置编码的行为。

只通过文字理解可能还不太够，欢迎大家尝试我为这篇博客写的 Notebook，通过动手做实验来加深理解。 https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/FourierFeature

推荐参考资料：

用代码示例理解核回归：https://towardsdatascience.com/kernel-regression-made-easy-to-understand-86caf2d2b844

直观理解 NTK: https://www.inference.vc/neural-tangent-kernels-some-intuition-for-kernel-gradient-descent/

傅里叶特征官方示例 PyTorch 实现: https://github.com/ndahlquist/pytorch-fourier-feature-networks/tree/master