随着视觉主干模型不断向 Transformer 靠拢,和 Transformer 配套的一些技术也从 NLP 社区涌入了 CV 社区。比如 Stable Diffusion 3 还在用标准 Transformer 那一套正弦位置编码,而其升级版 FLUX.1 就用上了旋转位置编码 (RoPE) , Lumina-T2X 模型甚至把 RoPE 的长度外推技术也从 NLP 社区搬了过来。在这篇博文中,我将站在一个对 NLP 技术了解不深的 CV 研究者的视角,较为详细地介绍一下 NLP 中 RoPE 相关的位置编码知识、RoPE 长度外推技术以及它们在 CV 里的应用。
长度外推,指的是使用在短序列上预训练的 Transformer 模型直接生成超出训练长度的长序列。类比到图像生成中,长度外推可以看成对模型所建模的图像分布做了一次超分辨率:比如模型训练时只见过 $256 \times 256$ 的图像,我们想直接用它生成 $512 \times 512$ 且同样清晰的图像。
推荐大家在阅读本文前先熟悉位置编码的基本原理,强烈推荐阅读 RoPE 提出者苏剑林的系列文章。
位置编码设计原则与 RoPE 的首次提出:https://kexue.fm/archives/8130
详细介绍 RoPE:https://kexue.fm/archives/8265
介绍长度外推的一项关键改进 (NTK-aware):https://kexue.fm/archives/9675 https://kexue.fm/archives/9706 https://kexue.fm/archives/9948
和这篇博文相关的两篇学术论文是:
YaRN,一种公认效果较好的长度外推技术:YaRN: Efficient Context Window Extension of Large Language Models (https://arxiv.org/abs/2309.00071)
Lumina-Next,前沿扩散 Transformer (Diffusion Transformer, DIT) 模型,采用了长度外推技术:Lumina-Next : Making Lumina-T2X Stronger and Faster with Next-DiT (https://arxiv.org/abs/2406.18583)
位置编码知识回顾
Transformer 中的位置编码
相比于此前流行的 CNN、RNN 模型,Transformer 的一大特点是其输出与输入次序无关。比如我们用 Transformer 建模文本的概率,那么模型会把「上海」和「海上」当成概率一样的词语。这也就是说 Transformer 无法从输入词元 (token) 的位置关系中获取信息。
如果让 Transformer 不输出信息聚合后的概率,还是保留输入词元的结构的话,那么打乱输入词元顺序就会同样地打乱输出词元顺序。模型依然无法获取输入词元间的位置关系。
为了把 1, 2, 3, 4 这样的位置信息输入进模型,标准 Tranformer 的做法是给不同位置的输入加上不同的位置编码。假设模型的中间变量都是二维向量,那么在句子中位置为 $k$ 的词元的位置编码是:
如果模型的中间变量都是 $d$ 维向量 (为了方便不妨认为 $d$ 是偶数),我们只需要把 $d$ 拆成 $d/2$ 组,每组用不同频率的三角函数即可。这样,长度为 $d$ 的词元在位置 $k$ 的位置编码是:
直观上来看,随着中间变量的维度越来越长,位置编码中对应的三角函数的频率不断变低,从一开始的 $1$ 逐渐靠向 $1/10000$。
上述公式来自论文,代码实现时要注意更多细节。比如有些代码中 $i$ 是从 $0$ 开始计数的。由于指数的分子的范围是从$0$到$d-2$,代码会把指数的分母也改成 $d-2$,保证最后一组三角函数的频率是 $1/10000$。
算出一个和输入词元向量等长的位置编码后,该编码会直接加到输入向量上。由于这种编码用了正弦函数,所以它被后续工作称为正弦位置编码。
相对位置编码与 RoPE
在设计位置编码时,最好能让编码传达词元的绝对位置和相对位置信息。比如句号会出现在文本结尾而不是文本开头,这一规律来自绝对位置信息;而每几个词元会组成固定的词组,与它们在整段文本中的位置无关,这反映了相对位置信息的意义。
正弦位置编码同时满足了这两个性质。首先,正弦位置编码的输入只有绝对位置,它本质上就是一种绝对编码。另外,根据三角函数和角公式,假设偏移 $\Delta k$ 是常数,那么$sin(\alpha-\Delta k)$可以由含 $\alpha$ 的三角函数的线性组合表示。这说明模型能够从正弦编码中部分了解到一些相对位置的信息。
作为绝对位置编码,正弦编码虽然能够表达一些相对信息,但是这些信息太隐晦了。并且,该编码只在输入时加入,可能在网络运算中途这些信息就消失了。我们能不能更加显式地用某种绝对位置编码建模相对位置关系呢?
在 Transformer 中,不同位置的词元仅会在注意力操作时做信息交互。观察下面的注意力计算公式,更具体一点来说,信息交互发生在注意力的 QK 内积时。我们可以在每次注意力操作前都给 $Q$, $K$ 里各个向量加上位置编码,保证相对位置信息能反映在注意力计算里。
苏剑林设计了一种新的位置编码:考虑 $Q$ 里位置为 $m$ 的向量 $\mathbf{q}_m$ 和 $K$ 里位置为 $n$ 的向量 $\mathbf{k}_n$,给位置为 $j$ 的向量右乘上复数 $e^{ij\theta}$,其中 $i$ 是虚数单位, $\theta$ 是一个角度。这样,复数下的 QK 内积结果为:
其中,$Re[]$是取实部,$*$ 为共轭复数。可以发现,内积结果也出现了位置编码 $e^{i(m-n)\theta}$,且编码的值仅取决于相对位置 $(m-n)$。因此,这种编码能够更加显式地在注意力运算里建模相对位置。
由于最终结果取了实部,所以上述所有运算都可以转换成实数域的操作。假设 $\mathbf{q}_m = (q_0, q_1)$ 只是一个二维向量,那么上述右乘位置编码的操作可以写成:
从几何意义上讲,这个操作其实是二维向量旋转。因此,这种位置编码被称为旋转位置编码(RoPE)。
和正弦编码类似,要把二维中间变量拓展成 $d$ 维时,只要分组讨论,改变每组的频率(这里的频率是角度 $\theta$)就行了。
角度 $\theta$ 的设计可以参考 Transformer 的正弦编码:对于第 $i$ 组,我们令 $\theta_i=1/10000^{2i/d}$
RoPE 和正弦编码有同有异。相同之处在于:
- 二者都是绝对位置编码,并通过编码公式的某些设计间接传递了相对位置信息。
- 二者用了同样的正弦编码方式:随着变量通道数的增大,对应位置编码的正弦函数的频率不断指数衰减。
不同之处在于:
- 正弦编码仅在模型输入时施加一次,RoPE 在所有自注意力计算时都施加。
- 正弦编码会生成一组编码向量,加到输入上。而 RoPE 是一种操作,它的几何意义是把注意力输入向量旋转一个角度。
用 RoPE 实现长度外推
现在,我们正式进入本文的正题:长度外推。长度外推严格来说是一类任务,并不一定要用外推的做法。它似乎最早出自论文 ALiBi (Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation)。正如论文标题所示,该任务的目的就是「短训练,长推理」:在短序列上训练后,不经额外训练或只需少量微调,让模型生成长文本。后来这种任务也被称为「上下文窗口拓展」(Context Window Extension),目的依旧是用已经训好的模型来生成更大的文本,只是不强调方法是外推。为了称呼方便,我们在这篇博文里将该任务统称为「长度外推」。
我们想一想,假设模型训练时最大文本长度是 $L$,现在要生成长度为 $L’$ 的句子 ($L’>L$),我们需要做什么呢?其实我们只要把代码写好,除了生成长度以外啥也不改就行了。
这样的话,模型在运行时究竟哪里发生了变化呢?根据我们之前的分析,Transformer 是不知道位置信息的,只有位置编码传递了位置信息。因此,增加了生成句子长度后,原本只见过位置在 $L$ 之内的位置编码,现在要尝试解读位置为 $L, L+1, …, L’ - 1$ 的位置编码。因此,如果除了修改生成长度外什么也不做,其实就是让模型把学到的位置编码知识外推。但很可惜,由于没学过这些训练集之外的位置关系,这种外推法效果很差。
我们在接下来的几节里会讨论一些更加强大的长度外推策略。这里先补充介绍一点东西。看了对长度外推任务的基本介绍,读者或许会疑惑:长度外推似乎只要考虑位置编号就行了,不是非得和 RoPE 绑定起来?其实,长度外推真正要考虑的是位置编码的形式而不是只考虑编号。我们稍后的分析其实对所有类正弦编码都有效。但现在大家都是基于 RoPE 讨论,用基于 RoPE 的模型做实验,可能是因为 RoPE 更加直接、全面地建模了词元间的交互关系,只要调整了 RoPE 的公式,其效果立刻就能反映出来。相比之下,正弦位置编码只是在输入时提供了位置信息,修改位置编码的细节不能全面地影响模型的输出。
位置内插
既然超出 $L$ 的位置没有被训练过,那么在 $L$ 之内多选一些位置为分数的点不就行了?位置内插(Positional Interpolation, PI)就是这样的一种长度外推方法,它把长度为 $0$~$L’$ 的位置线性压缩到 $0$~$L$ 内。也就是说,对于位置$m$,将其的位置编号修改为:
由于位置编号会被送进正弦函数里,所以编号哪怕是分数也没关系。通过这种简单的线性内插方法,我们就能在已经学好的编号范围内多选一些位置,实现长度外推。
内插确实比外推的效果要好得多。后续所有长度外推方法实际上都是在研究如何更好的求插值位置编码。很快,有人就从频率分析的角度提出了线性内插的一个改进。
改变正弦函数基础频率:NTK-aware Scaled RoPE
直观认识
就在位置内插提出不久,就有研究者在社区 (https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_scaled_rope_allows_llama_models_to_have/) 提出了一种效果更好,完全不需要微调的长度外推技术:NTK-aware Scaled RoPE (后文简称为”NTK-aware RoPE”)。该研究者后续将此方法进一步整理优化,发表了论文 YaRN: Efficient Context Window Extension of Large Language Models。我们先看一下 NTK-aware RoPE。
NTK-aware RoPE 的改动非常简洁,但它改动的地方却很出人意料:原来,总长度为 $d$ 的向量的第 $i$ 组位置编码的频率为:
现在,我们把 $10000$ 改掉,公式变为:
使用这种新长度外推方法,在上下文窗口大小为 2048 的 LLaMA 模型上,模型生成长文本的误差远低于之前的方法。
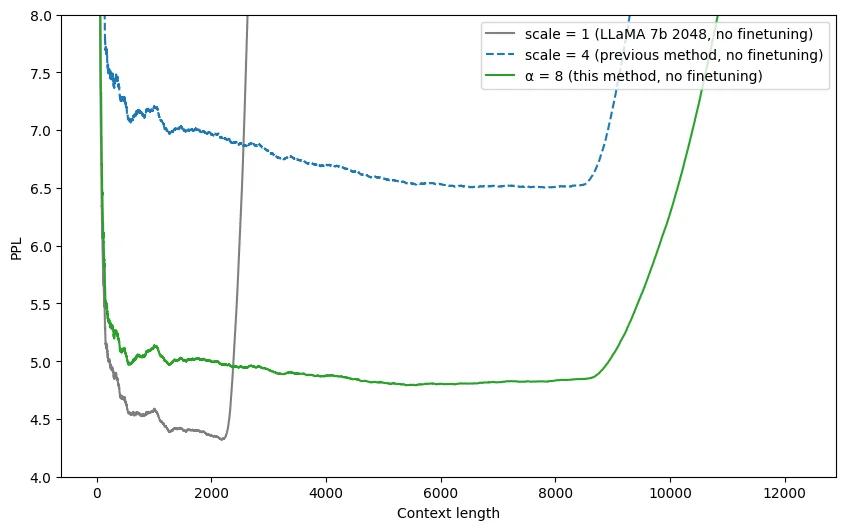
为什么这么简洁而奇怪的修改这么有效呢?在深入理解其原理之前,我们先直观地看一看这个方法具体修改了公式里的哪些参数。
先看新位置编码向量 $\sin m\theta_i^{NTK-aware}$ 的第二组(假设 $i$ 从 $0$ 开始计数),也就是含参频率最大的这一组。它现在是:
$\frac{L’}{L}$ 表示新长度是训练长度的几倍,它是一个大于 $1$ 的数。$d$ 在 LLaMA 里是 $128$,所以我们可以认为 $(d-2)$ 远大于 $2$。所以,$(\frac{L’}{L})^{(-2)/(d-2)}$ 这一项略小于 $1$。整体上看,这一改动差不多就是给三角函数的频率乘上了一个略小于 $1$ 的常数,几乎没变。
再看频率最小的 $i=d/2-1$ 项。它现在是:
而在线性内插中,我们直接把所有 $m$ 替换成了 $\frac{L}{L’}m$。所以,频率最小的项的公式和线性内插时的公式完全相同。
这里要澄清一下「外推」和「内插」的概念,这两个词的意义在很多博客和论文里并没有讲清楚。「内插」指的是通过像前面的线性位置内插一样,修改位置编号,使其恰好落在训练长度内。然而,一旦这个内插不够彻底,那么新位置编号就可能会超出训练长度,形成位置「外推」。我们本文讨论的所有方案,都是让不同频率的项在完全内插(恰好长度适合)和完全外推直接找一个平衡。一旦内插不彻底,就可以称为外推。所以很多文章里的「外推」,有的时候指的是不完全的内插。根据这样的术语定义,NTK-aware RoPE 的行为可以称为:最低频内插,其他频率外推。
从上面的分析可以看出,NTK-aware RoPE 还是沿用位置线性内插的思路,但是它对 RoPE 的影响更加平滑:对于位置编码高频项,公式几乎不变;对于最低频项,公式完全等于线性内插时的公式。
那么,NTK-aware RoPE 为什么有效呢?它又是怎么被想出来的呢?说起来,这个一直出现的 “NTK” 又是什么意思?NTK 其实是和神经网络相关的一种理论。NTK-aware RoPE 的提出者在构思这些公式时受到了 NTK 的启发,但他后续在论文里解释此方法时完全没有从严谨的理论入手,而只是讲了一些直觉的观察。在之后的两小节中,我将先从 NTK 理论的角度试图还原提出者的心路历程,再从一个广为人知、更易理解的角度来介绍 NTK-aware RoPE。
从 NTK 角度的解释
近几年和 NTK 理论比较相关的论文叫做 Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains。这篇论文用 NTK 理论分析了 NeRF 这种以位置坐标为输入的 MLP 需要位置编码的原因,并将这类位置编码归纳为「傅里叶特征」。
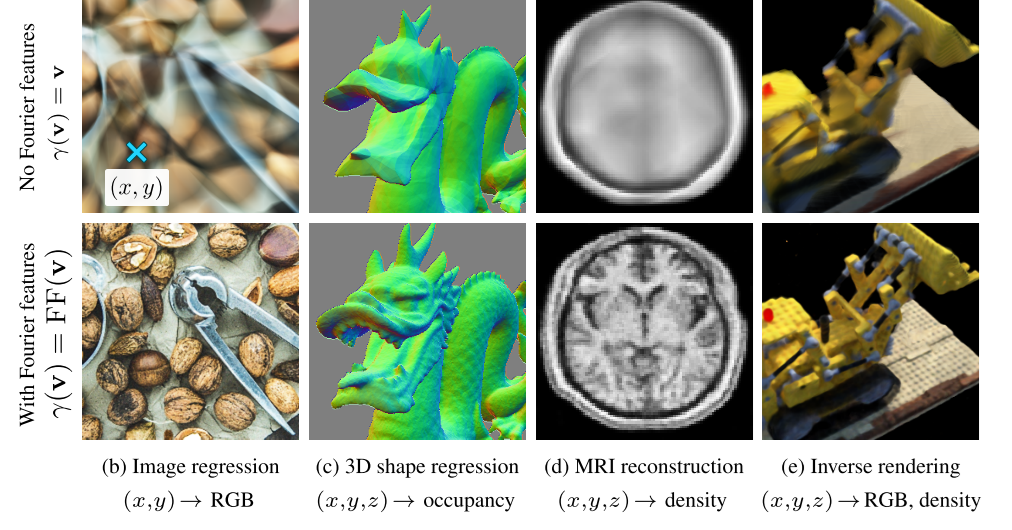
这篇论文最大的一个发现是:在形式为 $[\sin \theta_i x, \cos \theta_i x]$ 这样的傅里叶特征中,最重要的是决定最大频率。最大频率越大,MLP 拟合高频信息的能力越强。
由于 RoPE 的公式来自于正弦位置编码,而正弦编码又可以看成一种特殊的傅里叶特征,所以 NTK-aware RoPE 的提出者也试图将傅里叶特征中的规律套用在 RoPE 上。他可能观察到了应用线性内插后 RoPE 公式(正弦编码公式)的频率变化。原来编码第 $i$ 项为:
应用线性内插后,公式为:
这里 $\frac{L}{L’}$ 是一个小于 $1$ 的数。所以,加上线性内插后,所有项的频率都变小了。自然,公式能表达的最大频率也变小了,拟合高频信息的能力下降了。
我们可以把线性内插类比到 NeRF 这类任务中。如果我们增加输入坐标的密度,确实可以让图片/3D 模型的输出分辨率变大。但是,根据信号处理的知识,这种分辨率变大并不能超出原有的频率,所以变大后的图片/3D 模型会看起来很模糊。「模糊」在文本任务中的体现可能就是误差指标上升。
出于这些原因,NTK-aware RoPE 的策略是尽可能不动高频项的频率,仅动低频项的频率。当然,按照这种设计思路,我们其实可以提出各种各样的方案。NTK-aware RoPE 选了实现起来最方便的一种:修改频率基底,让它在最低频时和线性内插对齐(读者感兴趣可以设方程自行推导频率基底的修改值,把我们刚刚有关最低频项的分析倒过来)。这样,自然就有高频项几乎不变,低频项向线性内插靠拢,也就是我们在上一小节中的观察。
根据我的理解,傅里叶特征本身就只是稍微用到 NTK 相关的理论(参见我有关傅里叶特征的博文)。而 NTK-aware RoPE 的作者貌似仅是受到了傅里叶特征的某些启发,完全没有严谨地用 NTK 理论来推导 NTK-aware RoPE 的形式。所以,我认为,要学习 NTK-aware RoPE,完全不用学习 NTK 理论。
NTK-aware RoPE 的提出者在互联网上和 YaRN 论文中用了一些更好理解的方式解释 NTK-aware RoPE。类似地,从进制转换的角度,苏剑林也发表了两篇一针见血的解读博文:https://kexue.fm/archives/9675 https://kexue.fm/archives/9706 。我建议从这些角度来学习 NTK-aware RoPE,然后忘掉 NTK 这个词。我们在下一节里就从这个角度重新认识一遍位置编码。
从进制的角度解释
其实几乎每个人都理解位置编码。
不信?我来问个问题:看到 $1234$ 后,你看到了几个数?
确实,这只是一个数。但是,我们人在看到这个数的时候,其实是看到了 $4$ 个十进制数字。通过把不同位置的数字组合,我们才理解了这个数究竟是多少。真正的数是一个概念,我们可以把两个东西这一概念,表示成汉字「二」,阿拉伯数字「2」,或者是二进制下的 $10$。我们常见的十进制只是表达数的一种方式。
而进制表示其实就是一种表达数的位置编码。想象一个十进制计时器,它的数字从 $0, 1, …$ 开始不断增长。每隔 1 次,个位变一次;每隔 10 次,十位变一次;每隔 100 次,百位变一次……。也就是说,个位是频率最高的,位数越高频率越低。是不是这和正弦位置编码很像?正弦位置编码和进制表示的区别在于,进制用求余体现周期性,正弦位置编码用正弦函数体现周期性。
长度外推,就好像一个只见过 0-999 的模型,突然要处理 1000 以上的数一样。为了只用三位数来表达更大的数,一种简单的做法是进制转换。比如我们直接把十进制变成十六进制,那么可以表达的数就从 $10^3$ 变成了 $16^3$。
回到正弦编码的公式里,进制这个概念体现在哪呢?进制的底数又是什么呢?
在十进制里,不同位表示十、百、千……每算一个更高的位的值,就要多除以一次 $10$。所以,在正弦编码里,我们需要关注哪个被除以的量在做指数运算。通过观察发现,正弦编码的底数是 $10000^{2/d}$。
知道了我们想把句子长度拓展几倍,我们就可以精确地算出新底数。通过这种方式,我们就能推导出 NTK-aware RoPE。也就是说,NTK-aware RoPE 修改频率基底其实就是对正弦函数做进制转换。这部分推荐大家去阅读前面提到的苏剑林的博文。
基于数字进制,我们可以把位置编码类比成表示时间的时钟,便于后续概念的理解。这是因为:
- 正弦函数本身就可以用周期旋转来解释。
- 相比数字的进制,时间的进制的底数是不同的:1 天有 24 个小时,而一小时有 60 分钟。这提示我们:我们不一定要对每种频率做同样的处理。
利用这个时钟的比喻,NTK-aware RoPE 的提出者在社区解释了不应该像线性内插一样修改最高频率的原因:就像我们用秒针来区分最精确的时间一样,神经网络用最高频的正弦编码区分相对位置关系,且只能看清 1 秒以上的偏差。使用线性内插后,最小的时间偏差是 0.5 秒,神经网络就不能很好地处理最高频的那块信息了。而 NTK-aware RoPE 不会修改一秒的定义,只会在分钟、小时等更低频的分量上多插值一点,神经网络依然能区分最精细的时间。
改进 NTK-aware RoPE:分部 NTK
我们在上一节中学到,NTK-aware RoPE 的设计思想是高频不动(或理解成高频外推),只对低频内插。只改频率基底虽然做法简洁,但不见得是最优的做法。高频不动这部分应该没什么问题,我们把目光放在 RoPE 的低频分量上。
还是从十进制的角度看待位置编码。假设训练集的位置只有 $0$~$2800$,那么在千位上,模型只见过 $0, 1, 2$ 三个数字。由于在千位上模型没有完整见过 $0$~$9$ 的循环,模型不能推测出其他几个数字的意义。因此,在千位上做长度外推时,一定要用内插把位置编号正确缩放到已学习的范围内。
这套分析怎么迁移到正弦编码上呢?对于十进制数字,我们能很快判断出某一位是否走完了一个周期。比如要把千位上的 $0$~$9$ 都走一遍,就至少得要一万个数。怎么找出正弦编码每个频率走一个周期需要的距离呢?
在正弦函数中,我们可以用 $2 \pi$ 除以频率,得到波长。正弦位置编码某一项的波长表示当训练上下文长度至少为多少时,这一项会「转」完一个周期。比如时钟上,秒针 60 秒转一圈,分针 3600 秒转一圈。
$2 \pi$ 除以频率明明算出的是周期,周期乘上速度才是波长。但 YaRN 的作者就是在论文里把这个量定义成了周长。可能他们认为波长的单位是长度,上下文窗口大小也是长度,两个单位是匹配的。我认为这个名字取得很糟糕,就应该叫做周期的,只不过周期的单位也是长度而已。
根据这个定义出来的波长,我们可以对正弦位置编码的不同位置分类讨论:
- 如果波长过大,大于了训练时的文本长度,那么就用普通的线性内插,保证不在这些维度上外推。设它们的内插程度为 $1$。相比之下, NTK-aware RoPE 只对最低频项做了完整内插,而没有考虑其他波长过大的项也应该完整内插。
- 如果波长过小,说明频率很高,不应该做任何修改。设它们的内插程度为 $0$。
- 对于其他位置,根据它们的波长,线性选择内插程度。
这里波长过大、过小的阈值用超参数来决定,每个模型都需要手动调整。
总之,NTK-aware RoPE 只是模糊地定义了高频分量应该尽可能不变,低频分量应该尽可能像线性内插。而分部 NTK 则允许我们显式对各个频率分量做分类讨论。最终的位置编码方案 YaRN 在分部 NTK 的基础上还做了少许修改,对此感兴趣的读者可以去阅读论文。
图像生成中的 RoPE 与长度外推
了解了近年来 NLP 社区的位置编码技术,我们来以 Lumina-T2X 为例,再看一下这些技术是怎么用到视觉生成任务上的。
多维 RoPE
RoPE 本来是设计给 1D 的文本数据的。而在视觉任务中,图像是二维的,视频是三维的,我们需要设计更高维的位置编码。
回顾 RoPE 的形式:
要把它拓展成高维很简单。比如要拓展成 3D RoPE,只要把上面的公式复制两份,放到原公式的下面就行。也就是说,我们把向量拆成三份分别处理,每一部分和 1D RoPE 一样。
在这种设计下,模型所有中间向量的不同维度有了不同的意义,它们可能负责了视频宽度、高度或长度上的信息处理。我们也可以根据实际需要,让负责不同视频维度的向量长度不同。
视觉扩散模型中 RoPE 的长度外推设计
为了生成比训练分辨率更大的图像,Lumina-T2X 也参考了 NTK-aware RoPE,提出了一些和图像相关的 RoPE 改进策略。
首先,和分布 NTK 策略一样,Lumina-T2X 提出了频率感知 RoPE。在这种策略下,波长大于等于训练长度的位置编码项完全使用线性内推,剩下的项使用 NTK-aware RoPE。
另外,Lumina-T2X 还提出了时刻感知 RoPE。这个「时刻」指的是扩散模型里的加噪/去噪时刻。根据实验结果,Lumina-T2X 的作者发现线性内插会保持图像整体结构,但是图像局部质量下降;NTK-aware 策略提升了局部质量,却会出现内容重复现象,也就是全局关系不合理。能不能在某一方面结合二者呢?根据之前使用扩散模型的经验,扩散模型在去噪初期只生成低频信息,也就是全局信息,后期才会生成高频细节。受此启发,Lumina-T2X 提出了时刻感知 RoPE,该策略会在去噪早期仅使用线性内插,后续慢慢过渡到频率感知 RoPE。
以下是论文展示的在各种长度外推策略下生成 2K 图片的效果图。最左侧的 1K 图片供参考。

总结
长度外推是生成任务中的一项重要技术,它让我们在不大规模重新训练模型的前提下提升输出内容的长度/大小。而 Transformer 本身是一种无法获取输入元素位置信息的生成模型,需要靠额外的位置编码来感知位置。那么正好,只要我们能够适当地修改位置编码的推理行为,就能想办法让模型生成更长的内容。目前长度外推的方案都和修改 RoPE——一种给 Transformer 显式提供相对位置信息的位置编码——有关。我们主要学习了 NTK-aware RoPE 的设计原理,并通过深入的分析学习了其改进版分部 NTK RoPE。基于这些知识,我们简单认识了 RoPE 长度外推在视觉生成中的应用,其中比较有趣的一项设计是做长度外推时考虑扩散模型的去噪时刻。
说白了,本文所有长度外推设计都是在从两个维度上排列组合:RoPE 可以看成是由多个频率项组成的正弦编码;外推方案可以从位置编号线性内插过渡到位置编号不变(即位置外推)。一般的设计策略是:对于没有学满一个完整周期的频率项,采用完全线性内插;对于其余频率项,按一定比例执行线性内插。加上了扩散模型的去噪时刻这一设计维度后,我们可以按同样的设计思路,早期更关注低频,晚期更关注高频。
我觉得长度外推技术的能力是有上限的。我们完全可以从信号处理或者信息论的角度来思考这一问题,因为它的本质和从频域对图像做超分辨率很像。在较短的序列中,模型只能学到这种长度的序列所能表示的最大频率的信息。强行用它来生成更长的序列,只会出现两种情况:要么序列局部不够清晰,要么每个局部很清晰但是没有很好的全局依赖关系。根据信息论,模型就是不能从短序列中学到长序列蕴含的一些规律。从 Lumina-T2X 展示的结果里,我感觉 NTK-aware RoPE 的做法某种程度上就像是把全图做超分辨率变成拆成几个小图,每个小图在原来的训练长度上分别做超分辨率。这样最后图像每一块都很清晰,但合起来看就有问题。可能对于一些文本任务来说,只要局部质量高就行了,长距离依赖没那么重要。