今年年初,多尺度自回归模型 VAR 为图像生成开辟了新的发展方向:通过将图像生成建模成下一尺度预测,且每轮一次性生成同一尺度的所有像素,VAR 以极快的速度实现了高质量图像生成。随后,有许多工作都尝试对其改进。为弥补 VAR 中 VQ (Vector Quantization,向量量化) 操作引入的信息损失,HART (Hybrid Autoregressive Transformer,混合自回归 Transformer) 把 VQ 损失的信息用一张残差图表示,并用一个轻量的扩散模型来生成该残差图。做完改进后,作者用 HART 实现了 $1024 \times 1024$ 高分辨率文生图任务。在这篇博文中,我们将学习 HART 的核心方法并分析它在文生图任务上的实验结果。
论文链接:https://arxiv.org/abs/2410.10812
以往工作
本文涉及的所有自回归图像生成方法都起源于 VQVAE, VQGAN。在阅读本文前,建议读者先熟悉这两个经典工作。
HART 直接基于 VAR (Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction) 开发,且其部分思想和 MAR (Masked Autoregressive models,出自论文 Autoregressive Image Generation without Vector Quantization) 类似。欢迎大家阅读我之前的解读。
在 VQGAN 两阶段生成方法的基础上,VAR 让自编码器输出一系列不同尺度的图像词元 (token),而不仅仅是最大尺度的词元。生成时,VAR 自回归地生成不同尺度的词元图,同一尺度的词元图会在一轮 Transformer 推理中一次性生成。
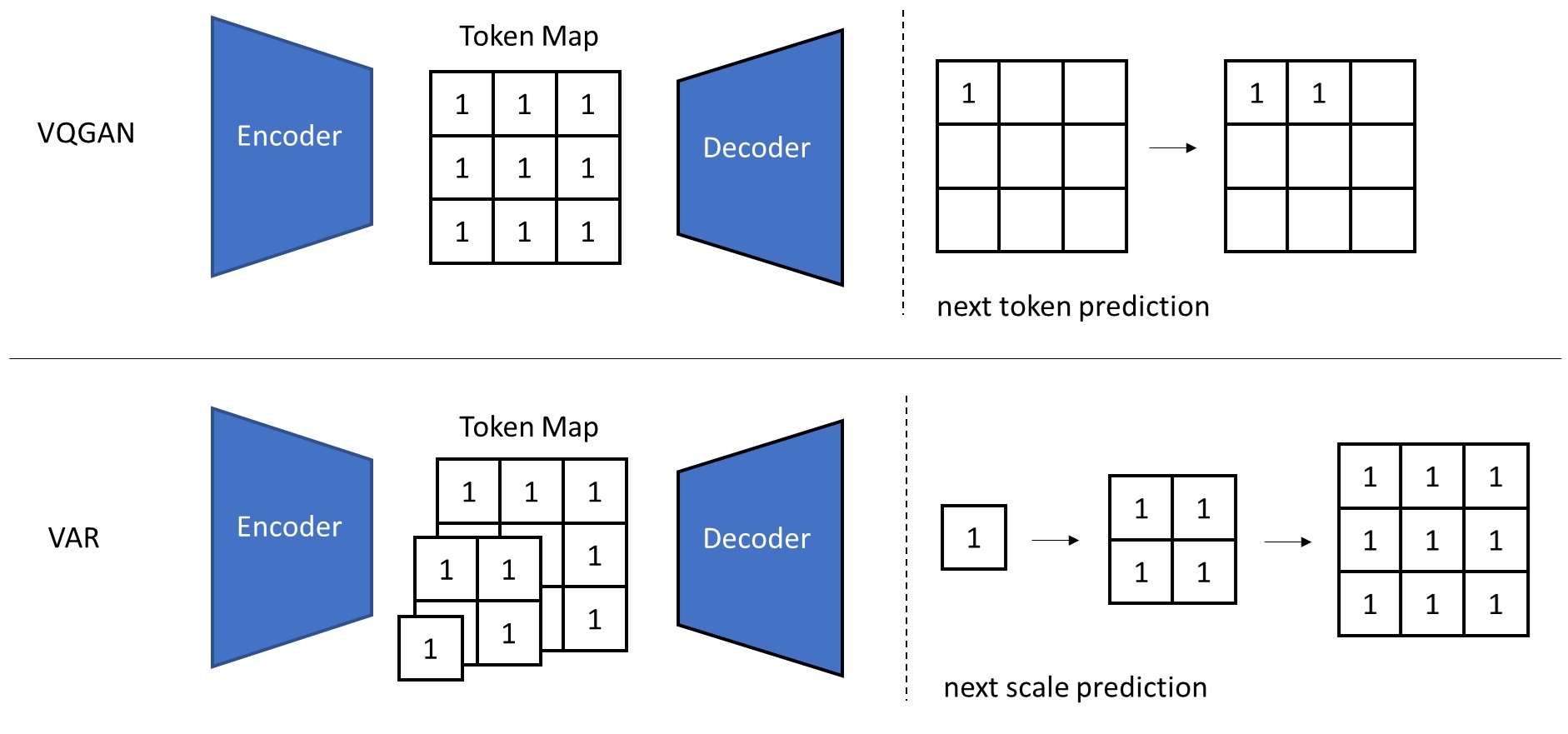
VQ 操作会丢失编码器输出中的信息,这导致所有使用 VQ 自编码器的图像生成模型生成质量略低。VAR, VQGAN 等方法之所以不得不使用 VQ,是因为这些方法都用类别分布(categorical distribution)来建模词元的分布。为了彻底去除 VQ 操作,MAR 使用扩散模型来代替类别分布,使得我们能够用精度更高的 VAE 来压缩图像。
弥补 VQ 的信息损失
为了缓解 VAR 中 VQ 造成的质量下降,HART 使用了一项思路直接的设计:既然 VQ 无论如何都会造成信息损失,不妨把损失的信息看成一张残差图像。用普通的 VAR 生成完图片后,再用扩散模型生成该残差图像。把残差图像加到原输出图像后,新输出图像会质量更高。
让我们通过论文里的图片来直观感受这一点。第一行是 VAR 自编码器和 HART 的混合自编码器的重建结果。可以看出,由于 VQ 操作,模型难以重建输入图像。第二行原 VAR 的输出和残差图像输出。我们发现,加上残差图像后,图像的细节更加丰富,不会像之前一样模糊。

在下两个小节里,我们来学习 HART 是怎么分别改进 VAR 的词元生成模型和自编码器的。
用扩散模型生成残差图像
为了理解整套方法,我们需要理解 HART 的「残差图像」是从哪来的。因此,我们先看词元生成模型上的修改,再看自编码器的对应修改。
我们先仔细回顾一下 VAR 中 VQ 误差是怎么引入的。VAR 借用了传统拉普拉斯金字塔的思想来建模不同尺度的词元图。

也就是说,VAR 并没有将完整图像拆解成内容相同、不同分辨率的词元图,而是拆解成了最低分辨率的图以及各个尺度上的信息损失。这里的信息损失不仅包括了下采样导致的,还包括了 VQ 导致的。
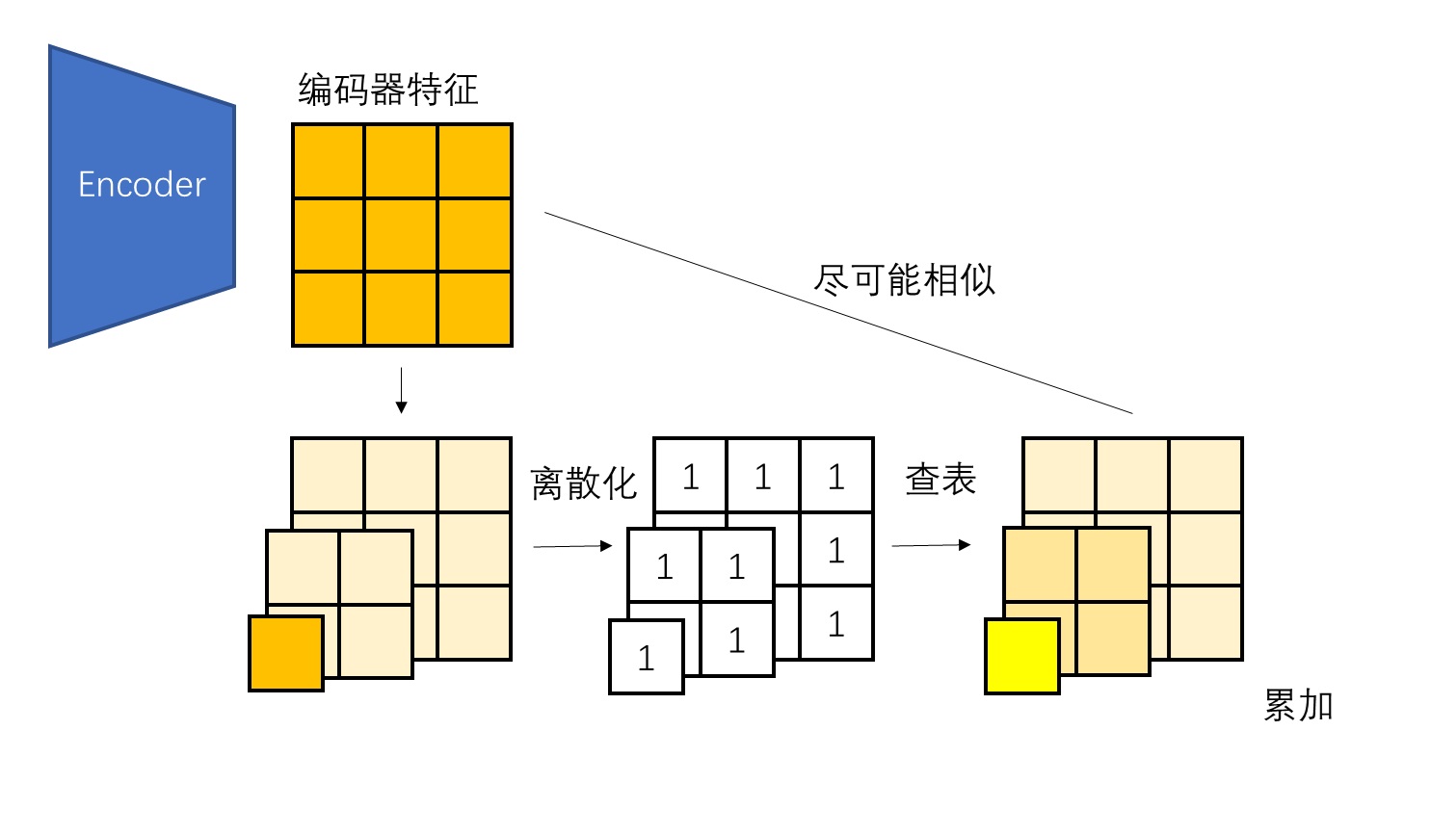
即使在多尺度拆解时考虑了 VQ 的信息损失,最终的重建特征(即解码器输入,词元查表输出的累加)依然不能和编码器输出特征完全一致。HART 想用扩散模型生成的「残差图像」,就是上图中重建特征和编码器输出特征的差。
和离散的词元图不同,残差图像是连续的。为了生成该连续图像,HART 参考 MAR,使用了一个图像约束的扩散模型。该任务可以解释为:已知离散词元图的输出,该如何用扩散模型生成细节,以提升输出图像质量。
HART 的生成模型示意图如下所示。前面的生成过程和 VAR 一模一样。在最后一步,Transformer 的中间隐状态会输入给用 MLP 表示的扩散模型,扩散模型会为每个词元独立地预测残差量。也就是说,这不是一个图像扩散模型,而是只生成一个词元值的像素扩散模型。词元之间的采样互相独立。得益于这种独立性假设,HART 可以用一个非常轻量的扩散模型来生成残差图,几乎没有增加整体的生成时间。

HART 还将 VAR 的类别约束换成了文本约束。我们稍后在实验部分讨论。
AE + VQVAE 混合自编码器
知道了 HART 要生成的残差图像从何而来,我们可以回头学习自编码器上的对应修改。现在,自编码器的解码器有两种输入:一种是 VAR 离散词元累加而成的近似重建特征,一种是加上了 HART 的残差图的精确重建特征,这个重建特征就等于编码器输出特征。为了同时处理这两类输入,在训练 HART 的混合自编码器时,解码器的输入一半的时候是编码器输出,另一半的时候是离散词元的重建特征。当然,在生成时,由于加上了残差图像,可以认为解码器的输入就等于编码器的输出。
下图中采用的术语 token 与 VAR 不同。VAR 把编码器输出和解码器输入都叫做特征图 (feature map),把过了 VQ 操作的索引图叫做词元图 (token map)。而 HART 将 VAR 里的特征图称为 token,continuous token 表示编码器输出特征,discrete token 表示词元的重建特征。这篇博文采用了 VAR 的称呼方法。同理,HART 里的 residual token 在本文被称为「残差图像」。
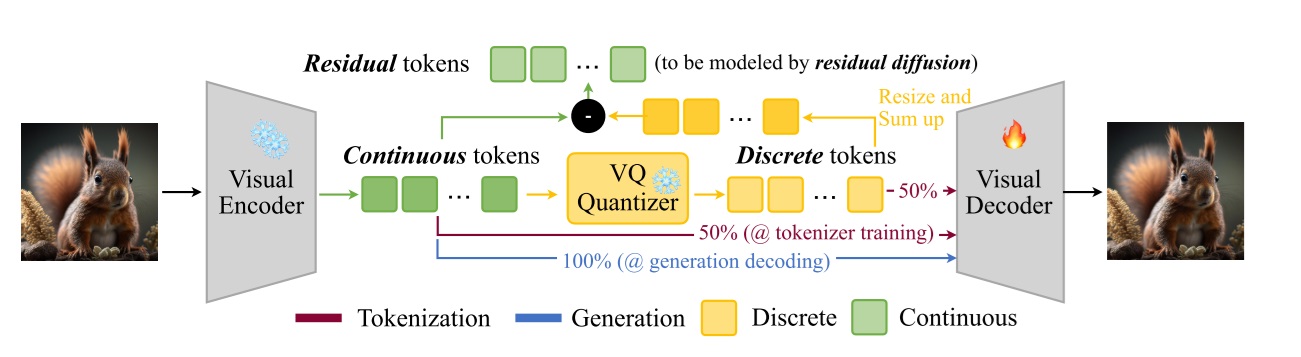
这样看来,HART 的混合编码器既像没有 KL Loss 的 VAE,即普通自编码器 (AE),也像 VQVAE。
高分辨率文生图实现细节
我们来简单看一下 HART 是如何把 ImageNet $256 \times 256$ 按类别生成的 VAR 拓展成 $1024 \times 1024$ 的文生图模型的。
- 文本约束:HART 没有通过交叉注意力输入文本信息,而是和 VAR 对类别嵌入的做法一样,将文本嵌入作为第一尺度的输入及 AdaLN 层的输入。
- 位置编码:不管是对于尺度编号还是图像位置编号,VAR 用的是可学习的绝对位置编码。HART 对尺度采取了正弦编码,对图像词元采取了 2D RoPE(旋转位置编码)。
- 更大尺度:原 VAR 词元图的最大边长是
16,HART 往后面添加了21,27,36,48,64这几个边长。 - 轻量级扩散模型:由于扩散模型仅需建模单个词元的分布,它仅有 37M 参数,只需 8 步就能完成高质量采样。
定量实验结果
先看一下最热门的「刷点」指标——ImageNet $256 \times 256$ 按类别生成。作者没放最好的 MAR 模型,我补上去了。
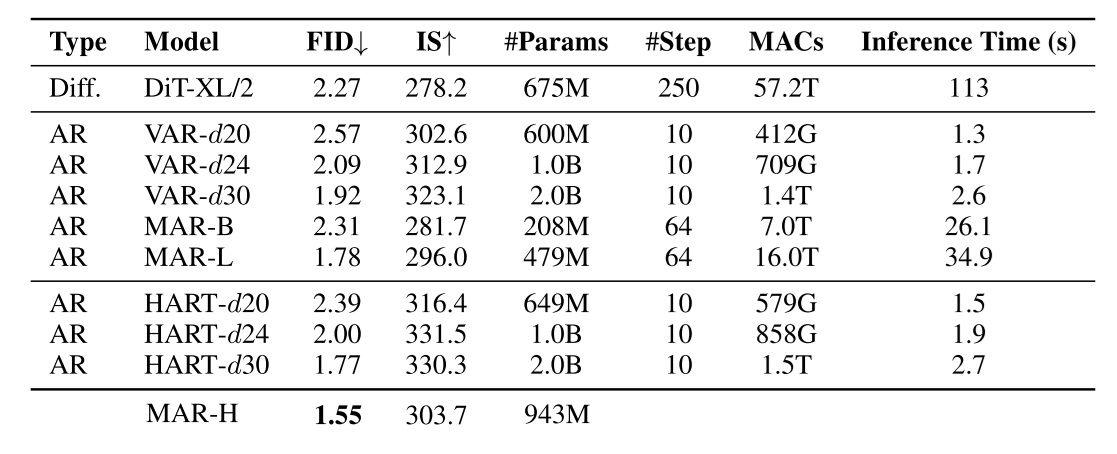
在这个任务上,HART 和 VAR 的主要区别在于是否使用扩散模型输出残差图像。从结果可以看出,残差扩散模型几乎没有提升推理时间,却对 FID 指标有不小的提升(考虑到数值越低,提升难度越大)。并且,通过比较不同模型的速度,我们发现类 VAR 模型最大的优势在于推理速度快。
再看一下这篇论文重点关注的文生图指标。除了常用的主要衡量文图匹配度的 GenEval 外,论文还展示了两个今年刚出的指标: MJHQ-30K 数据集上的指标和 DPG-Bench。
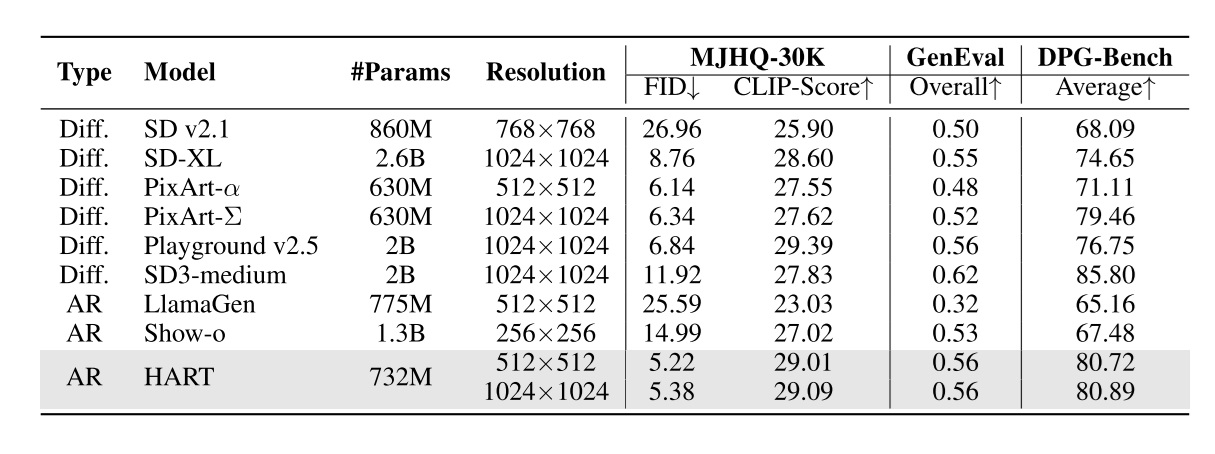
这些指标不见得很有说服力。在由用户投票的排名中 (https://imgsys.org/rankings),Playground v2.5 最好,SD3 和 PixelArt-Σ 差不多。但是,MJHQ FID 和 DPG-banech 指标都不能反映出这些模型的排名。特别地,FID 用到的 Inception V3 网络是在 $299 \times 299$ 的 ImageNet 上训练的,所以 FID 既不能很好地反映高分辨率图像的相似度,也不能反映更复杂的图像的相似度。
综上,HART 在高分辨率文生图任务上的表现暂时不能通过实验结果反映。根据部分社区用户的反馈(https://www.reddit.com/r/StableDiffusion/comments/1glig4u/mits_hart_fast_texttoimage_model_you_need_to_see/ ),HART 在高频细节的生成上存在缺陷。通过回顾 HART 的方法,我们可以猜测这是残差扩散模型的设计不够好导致的。
总结
为了缓解 VQ 自编码器中 VQ 操作带来的信息损失,HART 把信息损失当成一张残差图,并额外用一个轻量级像素扩散模型来独立地生成残差图的每个像素。HART 把这一改进直接应用到了 VAR 上,并提升了 VAR 的 ImageNet FID 指标。HART 在高分辨率文生图任务上依然无法媲美扩散模型,并且由于扩散模型存在诸多加速手段,它在生成速度上也没有优势。
VQ 操作将复杂的图像转换成了易于学习的图像词元,但牺牲了自编码器的重建质量。为了改进这一点,有许多工作都试图改进原 VQVAE 的最近邻 VQ 操作。但无论如何,VQ 导致的误差是不可避免的。HART 从另一个角度缓解 VQ 重建误差:用另一个模型来生成残差图像。这种设计思想很有前途,有希望彻底去除 VQ 的误差。然而,天下没有免费的午餐,提升了生成效果,就不得不增加训练和生成时间。HART 用轻量级像素扩散模型生成残差图的做法虽然不会拖慢模型速度,但效果还不够好。或许可以将其换成一个感受野稍大一点的扩散模型,在不显著增加生成时间的前提下提升残差图生成效果。