CFG-Zero*：流匹配时代的新版 Classifier-Free Guidance

如果你玩过图像扩散模型，那你一定不会对 “guidance_scale=7.5” 这个参数感到陌生。这个 “guidance” 指的就是 Classifier-Free Guidance (无需分类器指引，CFG)。忽略其背后的数学原理，CFG 的作用和公式其实非常易懂。假设 $F(x, c)$ 是一个输入为图像 $x$ 和约束 $c$ (比如文本) 的神经网络，则使用 CFG 后的结果 $\tilde{F}(x, c)$按下面的公式计算：

$$\tilde{F}(x, c) = (1-w) \cdot F(x, \emptyset) + w \cdot F(x, c)$$

其中，$w$ 是指引强度，在 Stable Diffusion 常取 7.5 的强度参数就是这里的 $w$。直观上看，通过增加 $w$ 的大小，我们可以让 CFG 结果更靠近带约束的输出 $F(x, c)$，更远离无约束的输出 $F(x, \emptyset)$。比如 $w=0$ 时，CFG 结果就是无约束输出 $F(x, \emptyset)$；$w=1$ 时，CFG 结果就是带约束输出 $F(x, c)$。在约束 $c$ 为文本的文生图扩散模型中，我们常常可以通过调整这个参数，来提升图像与输入文本的匹配程度。

在 CFG 中，$F$ 可以是任何一个神经网络。比如，它可以是 DDPM 中预测噪声的网络 $\epsilon$，也可以是流匹配中预测速度的网络 $v$。甚至在一些没有用到扩散模型，但是输入中包含 $c$ 的自回归模型中，我们也可以用到 CFG。

但是，上面的 CFG 公式还有没有改进空间呢？近期，以 NTU S-Lab 博士生范洧辰主导的工作探究了一种专门为流匹配 (Flow Matching) 打造的改进版 CFG—— CFG-Zero*。

这个方法可以提升所有流匹配模型的生成质量，比如文生图模型 SD3, FLUX.1，以及视频生成模型 WAN-2.1。以下是 SD3.5 上的实验结果。

由于 CFG 的原理比较简单，在这篇博文中，我会跳过背景介绍，直接讲解 CFG-Zero* 的方法及主要消融实验结果，并给出我对该论文的看法。

项目网站：https://weichenfan.github.io/webpage-cfg-zero-star/

GitHub: https://github.com/WeichenFan/CFG-Zero-star

CFG-Zero* 方法讲解

CFG-Zero* 由两个相对独立的改进组成：

1. 给 CFG 公式中多乘上一个系数
2. 在流匹配采样的早期不更新带噪图像

我们来分别学习这两项改动的原理。

改进版 CFG 公式

作者认为，应该在 CFG 中添加一项能够调节无约束和带约束输出相对大小的缩放系数 $s$。按照前文的 CFG 公式，对于输出 $t$ 时刻速度的流匹配模型 $v_t^{\theta}(x, c)$，改进版 CFG 的输出应为：

$$\tilde{v}_t^{\theta}(x, c) = (1-w) \cdot s \cdot v_t^{\theta}(x, \emptyset) + w \cdot v_t^{\theta}(x, c)$$

也就是说，我们在原来 CFG 公式的 $v_t^{\theta}(x, \emptyset)$ 前多乘了一个标量 $s$。

此外，作者还认为，最优情况下，$s \cdot v_t^{\theta}(x, \emptyset)$ 和 $v_t^{\theta}(x, c)$ 应该尽可能接近。即 $s$ 满足

$$\min_s|| s \cdot v_t^{\theta}(x, \emptyset) - v_t^{\theta}(x, c)||_2^2$$

上述两个假设是怎么得出的？在理解公式的原理之前，我们先看一下这个公式的几何意义，再反过头倒推其原理。

我们不妨将 $v_t^{\theta}(x, \emptyset)$ 和 $v_t^{\theta}(x, c)$ 看成平面上的向量。

给 $v_t^{\theta}(x, \emptyset)$ 添加一个系数，就意味着 $s \cdot v_t^{\theta}(x, \emptyset)$ 可以是其所在直线上的任何一个向量。

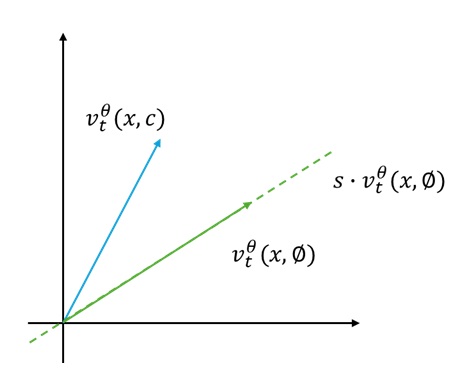
什么时候向量 $s \cdot v_t^{\theta}(x, \emptyset)$ 与 $v_t^{\theta}(x, c)$ 距离最短呢？当然是 $s \cdot v_t^{\theta}(x, \emptyset)$ 正好位于 $v_t^{\theta}(x, c)$ 在 $v_t^{\theta}(x, \emptyset)$ 上的投影处。

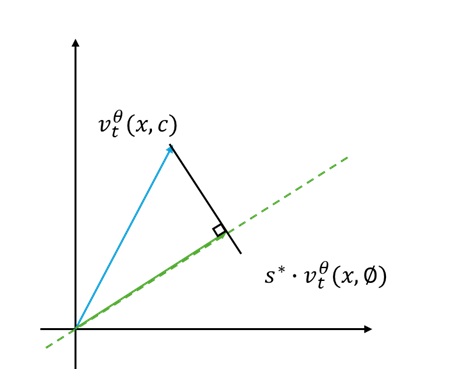
此时 $s$ 的取值 $s^*$ 可以通过求向量内积再除以原向量的模得到。

$$s^* = \frac{v_t^{\theta}(x, c)^T v_t^{\theta}(x, \emptyset)}{||v_t^{\theta}(x, \emptyset)||^2}$$

了解完改进版 CFG 优化目标的几何意义后，我们再来尝试倒推它的两项设计：1）为什么要乘 $s$；2）为什么要令两个向量的距离最短。

CFG 的目的就是让带约束输出能够尽可能远离无约束输出。标准的 CFG 只告诉我们如何让某一个点 （带约束输出）远离另一个点（无约束输出）。现在，假如无约束输出是一条直线，那我们应该以「最快」的方向让带约束输出远离这条直线。这里的「最快」方向其实就是点对直线做垂线所在方向。

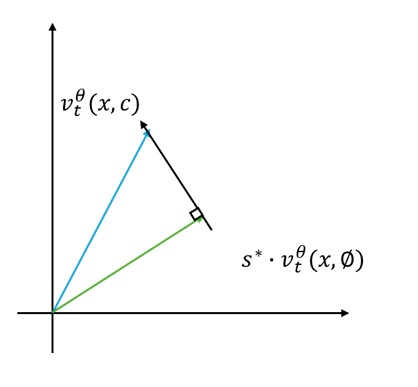
根据上述分析，我们解释了第二项设计：令向量距离最短，本质原理是找到一个让带约束输出远离无约束输出所在直线的「最快」方向。

那么，第一项设计又如何解释呢？为什么可以给无约束输出多乘一个系数呢？这就很难给一个严谨的解释了。我们只能猜测，对于输出速度的流匹配模型来说，无约束输出的速度的方向比速度的大小更加重要。因此，我们不仅要远离此时无约束的输出，还要远离无约束输出所在直线（所有速度方向相同的点）。

关于这两项假设，作者在论文中做了一定的解释。

对于为什么要乘 $s$，作者认为这是受到 classifier guidance 的启发。在 classifier guidance 中，无约束项和梯度项（在 CFG 中梯度项即为带约束输出）之间是有一个自定义参数 $s$ 来调节它们的相对比例的。CFG 本来就是 classifier guidance 的一种特殊形式，自然也可以用上这个设计。这样看来，作者也没能从理论上讲清为什么要乘 $s$，只是参照以往工作，尝试性地使用了这项改动。

对于在求解 $s$ 时为什么要令两个向量的距离最短，作者解释如下：假设最优情况下，ground truth 输出应为 $v_t^{*}(x, c)$，那么我们应该最小化改进版 CFG 输出 $\tilde{v}_t^{\theta}(x, c)$ 与其的距离（参数 $s$ 为变量）。

$$L(s) = || \tilde{v}_t^{\theta}(x, c) - v_t^{*}(x, c)||_2^2$$

上式其实描述了两个向量之间的距离。根据三角不等式（三角形两边之和不小于第三边），可以估算其上界：

$$L(s) \leq || \tilde{v}_t^{\theta}(x, c) ||_2^2 + || v_t^{*}(x, c)||_2^2$$

所以问题变成了令 $\tilde{v}_t^{\theta}(x, c)$ 的模尽可能小，也就是令改进版 CFG 里两个向量距离尽可能短。按照我们上文的几何分析，就可以求出最优的 $s$。

我认为上述分析非常牵强。作者引入 GT 输出 $v_t^{*}(x, c)$，只是为了说明模型输出和 GT 的距离的上界包含 $\tilde{v}_t^{\theta}(x, c)$ 的模。可是，优化上界，真的就能优化这个值本身吗？这无法从理论上说明，只能通过实验来验证。应该令 $\tilde{v}_t^{\theta}(x, c)$ 的模尽可能小，同样是一个实验性的结论。

零初始化流匹配早期输出

在简单的高斯混合任务，即从带噪分布 $\mathcal{N}(0, \mathbf{I})$ 生成目标分布 $\mathcal{N}(\mu, \mathbf{I})$ 上，我们可以直接求出流匹配的闭合解。因此，在这种简单任务上，我们可以训练流匹配网络，观察它和流匹配闭合解的误差，进而研究流匹配网络的学习规律。

通过这种研究方法，作者发现了另一个规律：训练刚开始时，在流匹配的开始阶段（即图像为高斯噪声的阶段），网络预测的速度 $\tilde{v}_0^{\theta}$ 非常不准确，甚至不如直接输出 $0$ 向量。只有得到充分训练后，网络的预测值才比输出 $0$ 更好。

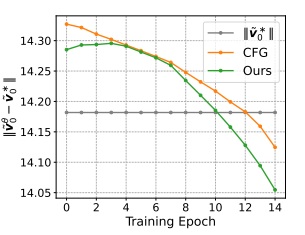
在更大的 ImageNet 数据集上，该结论同样有效。

我们可以猜测，现在大型文生图模型或者视频模型都没有充分收敛。因此，我们可以对这些模型做一个非常简单的改进：跳过刚开始几次去噪步骤（即让流匹配输出 $0$ 向量），让纯高斯噪声从某个中间时间步开始去噪。

实验

把 CFG 公式改进，并且加入零初始化后，我们就得到了最终的 CFG-Zero*。作者用大量定性和定量实验证明了 CFG-Zero* 能够从多个指标上提升各类流匹配模型的效果。网上有许多 AI 应用博主分享了 CFG-Zero 的使用效果 （感兴趣的读者可以去 Bilibili 搜索 CFG Zero Star），发现它确实能够增强图像细节。在社区中，CFG-Zero 也广受好评，被加入了各个流匹配模型代码仓库的官方实现中。

在这篇博文中，我们主要关注 CFG-Zero* 的消融实验，并分析它们是怎么支持前文的方法的。

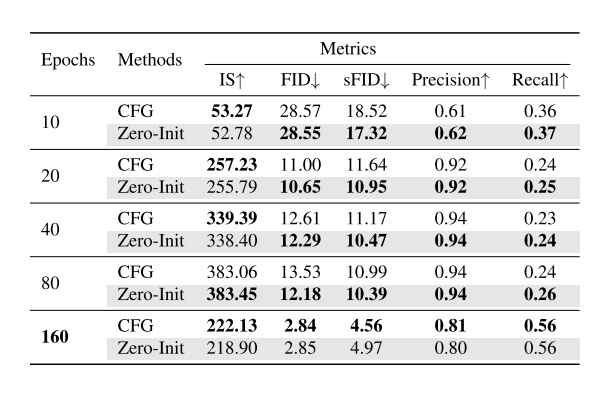
在消融实验一节中，作者首先展示了不同采样配置下，CFG-Zero 相较普通 CFG 的表现。这里的采样配置包括不同的采样步数、不同的 CFG 强度。从图中可以看出，CFG-Zero 在多数情况下都有优势，但数值上不是很明显。

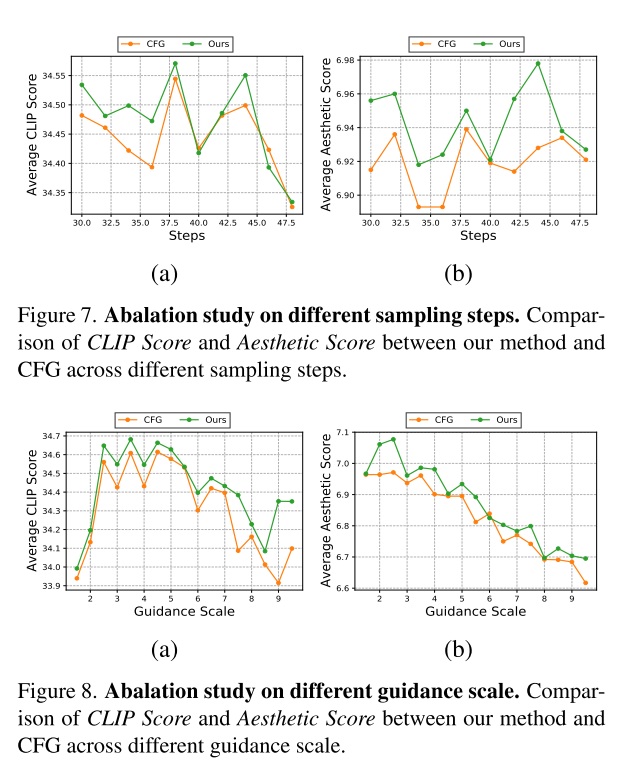
由于 CFG-Zero* 实际上由两个独立的方法组成，我们需要分别验证它们的有效性。作者同样给出了相关表格。可以看出，这两个方法都有用，但数值提升不是很明显。并且，不用零初始化，只加入缩放参数的提升似乎非常微小。

论文里还有一个应该对刚开始多少步做零初始化的拓展消融实验。这个实验和原理验证关系不大，在此略过。

仅从这些实验结果中，我感觉 CFG-Zero 在这几项指标上的提升非常不明显。我猜想 CFG-Zero 的作用可能更需要通过定性结果来反映，在一些普通 CFG 生成得不理想的例子上，CFG-Zero* 或许能够做好，就像论文开头展示的对比结果一样。

以上是论文里展示出的消融实验。但在我看来，为了支撑方法中的假设，论文还需要提供更多的实验结果：

• 为了证明优化 $|| \tilde{v}_t^{\theta}(x, c) ||_2^2 + || v_t^{}(x, c)||_2^2$ 这个上界，就能优化最后的误差 $|| \tilde{v}_t^{\theta}(x, c) - v_t^{}(x, c)||_2^2$，应该展示一个折线图，说明随着 $|| \tilde{v}_t^{\theta}(x, c) ||_2^2$ 变小，误差也能变小。另外，此时 $\tilde{v}_t^{\theta}(x, c)$ 其实不仅可以是 CFG 结果，还可以是带约束或者无约束的结果。
• 为了证明 $s=s^*$，即沿着垂线方向远离无约束输出是最好的，应该展示一个折线图，表示不同 $s$ 取值下和和 GT 误差的变化。
• 文章多次强调这些优化是针对流匹配的，但是没有从原理上讲为什么这些方法用不到 DDPM 上，也没有展示任何相关实验结果。

如果是作为一篇面向应用的论文，文中的实验结果是非常完备的。但从理论贡献上看，如果能够多展示一些支持理论分析的实验，文章就能给读者带来更多启发。

总结

CFG-Zero 是一种针对流匹配设计的即插即用的改进版 CFG。它由两个独立的部分组成：1）给无约束输出添加缩放系数；2）跳过开始几步流匹配去噪步骤。实验表明，CFG-Zero 无论是在文生图模型还是视频模型上都表现得很好。目前，CFG-Zero* 已经加入了 Diffusers 框架，并被各个主流流匹配官方仓库使用。

CFG-Zero 论文的主要贡献是提出了一种实用的流匹配采样增强方法。对于这类方法，用户会希望方法尽可能不需要训练，且效果尽可能好。CFG-Zero 完美契合了这两个条件。可以预见，CFG-Zero* 将成为未来流匹配模型的标配。

CFG-Zero* 论文的另一大贡献是提供了一种分析流匹配模型的方法，即在简单的高斯分布生成任务上，比较深度学习模型和闭合解之间的误差，探索模型的学习规律。基于这种研究方法，论文发现流匹配模型在去噪初期预测结果极其不准这一现象，比巧妙地用零初始化提升了推理的速度和质量。

尽管论文提出了一种 CFG 改进公式，但这套公式背后的原理还没有完全被该论文揭示。后续可能可以探索的点有：

• 这套方法是否能用到 DDPM 或者其他加噪公式或者预测目标上？如果不能，是哪一个区别导致的？
• 当前系数 $s$ 的选择真的是最优的吗？除了给无约束项添加系数，有没有其他的 CFG 改进方法？

在分析这篇文章的理论时，我再次感受到了目前深度学习方法面临的窘境：多数有效的方法难以详尽地解释清其原理，很多重要步骤完全是由实验结果决定的。比如 DDPM 中，前面算变分上界算得好好的，到最后一步算损失函数时，突然就把系数省略了。很多方法看上去有一套严密的数学公式，但实际上其中存在若干难以解释的步骤，而往往这些通过实验得到的步骤才是方法成功的关键。所以，在学习这些看起来很复杂的方法时，除了一股脑地接受论文里的推导外，我们也要仔细审视推导中究竟哪些步骤其实是存在逻辑跳跃，是由实验决定的。