近期何恺明团队的论文提出了一种叫做 Just image Transformers (JiT) 新式 DiT (Diffusion Transformer)。它的核心思想是:如果让扩散模型的预测目标从速度变成清晰图像,我们就能成功训练出一个像素空间 (pixel space) 的高分辨率 DiT,且无需对 DiT 结构做复杂的改进 。我这段时间也在做像素空间的 DiT,对这篇文章很感兴趣,立刻在我的实验环境下复现了 JiT。结果发现,我没能正确理解文章的贡献:JiT 论文表明,仅仅在 Transformer 的 patch size 较大 时,预测清晰图像才比预测速度更好。
在这篇博文中,我不会按照原论文的叙述逻辑,而是会根据我对这个领域的理解和实验过程,来逐步讲解 JiT 论文的发现,并给出我自己的分析。
高分辨率扩散模型的探索
最早的扩散模型
自从被提出以来,扩散模型最遭人诟病之处就是它的计算效率:无论是训练和推理,扩散模型都比之前的 GAN 要慢很多。这可以从早期的 ADM 模型的实验表格中反映出来。ADM 模型出自大名鼎鼎的论文 “Diffusion Models Beat GANs on Image Synthesis”,这篇论文在扩散模型奠基之作 DDPM 的基础上对 U-Net 去噪网络略加优化,并提出了 Classifier Guidance 这种优化条件生成 (conditional generation) 质量的方法。基于这些改进,论文在 ImageNet-256 上训练了一个进阶版 DDPM,也就是 ADM。它的结果如下,其中 Compute 的单位是 1 个 V100 运行一天能完成的计算量。
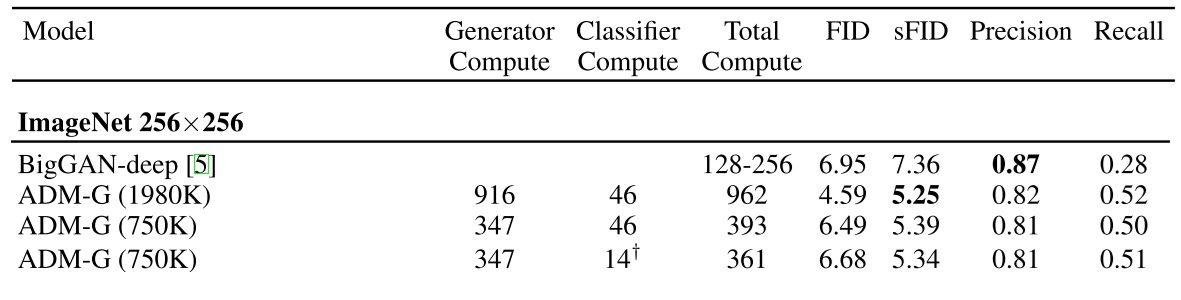
我们可以主要看 Total Compute 和 FID 这两列。最好的 ADM 要花 962 个 V100 天才能训练出一个 FID = 5.25 的模型。而现在,有了 latent space 的 DiT 后,哪怕是学校实验室的研究者也可以用一个多卡主机在一周内训练出一个 FID = 2 左右的模型。可见,早期扩散模型的学习效率是很低的。
LDM
为了提升扩散模型的推理和训练效率,Latent Diffusion Models (LDMs) 将之前 VQVAE, VQGAN 的两阶段生成方法引入了扩散模型中。LDM 会先训练一个能够压缩和复原图像的 VAE,再训练一个生成 VAE 潜空间 (latent space) 里的潜图像的扩散模型。由于潜图像的元素数远少于像素图像的元素数,LDM 的训练十分高效。
后续的 DiT 工作将 LDM 里的 U-Net 升级成了 Transformer。DiT 的名字虽然叫 Diffusion Transformer,但这篇论文依然沿用了 LDM 的两阶段设计,准确来讲它是一个 latent Diffusion Transformer。
在 DiT 论文的 ImageNet-256 benchmark 表格中,我们能看到 LDM 比像素空间的 ADM 更好,而用了 Transformer 的 DiT 比用 U-Net 的 LDM 更好。
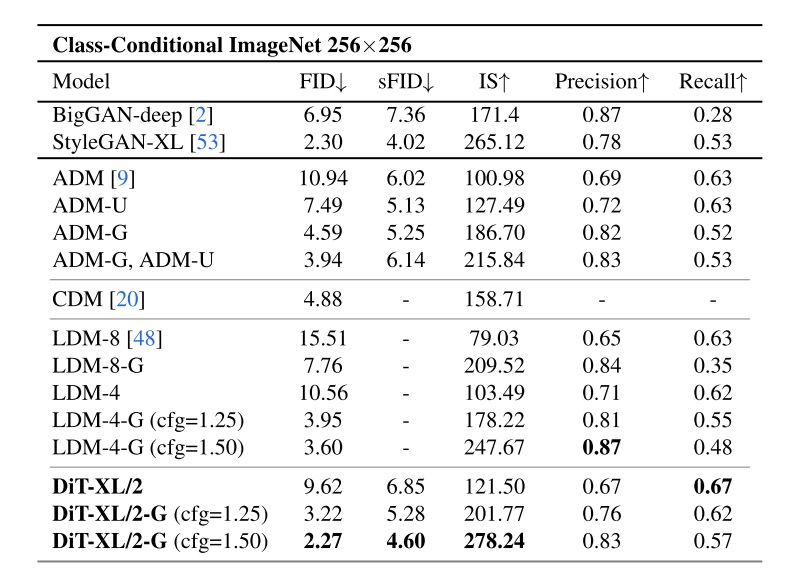
像素空间扩散模型的后续研究
LDM 虽然大大提升了扩散模型生成高分辨率图像的效率,但它并没有解决用扩散模型生成长序列这件事——因为 LDM 是通过减少潜图像序列的长度来提升效率的。但当输入序列变长,比如要生成视频时,我们仍然绕不过长序列生成这个问题。因此,继续研究像素空间的扩散模型仍有价值。
为什么像素空间的 ADM 的生成质量不够好呢?后续研究发现,为了让扩散模型每个时刻的信噪比不随序列长度变化,随着输入序列长度的增加,应该逐步增强噪声。如下图所示,同样添加标准高斯噪声,观察第一行 $64 \times 64$ 的带噪图像和第二行 $128 \times 128$ 带噪图像 average 下采样 2 倍后的输出,我们发现 $128 \times 128$ 明显看起来噪声更少,信息更多。这时,给噪声 $\times 2$ 后,它的信噪比就和 $64 \times 64$ 时差不多了。

像素空间扩散模型 Simple Diffusion (SD) 以及 Simple Diffusion 2 (SiD2) 基于这一观察,调整了加噪的方式。此外,它们也把 U-Net 升级成了和 Transformer 更像的 U-ViT。最终,SiD2 在 ImageNet-256 benchmark 上取得了很不错的表现。
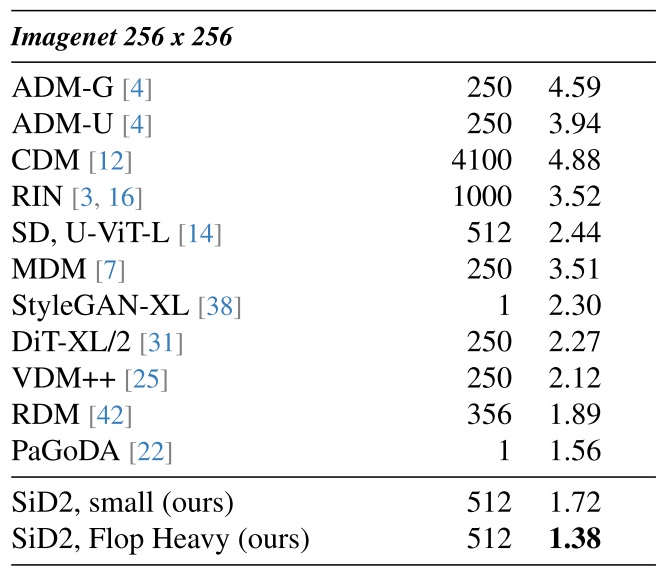
现在主流扩散模型主要参考了 Stable Diffusion 3 (SD3) 的噪声调整方式,会使用 logit-normal 采样而不是均匀采样来获取训练时的 t。
Pixel DiT
在前面的对比实验中,我们发现,在潜空间里 Transformer 比 U-Net 好。而之前像素空间的工作都用的是 U-Net,能否在像素空间里也用 DiT 呢?实际上,在 2025 年 10 月之前,研究 Pixel DiT 的工作非常少。这是因为 Transformer 的计算复杂度很大,我们必须用某种方式来压缩输入序列。但这些压缩往往会严重影响生成质量。
说起压缩序列,最常见的做法是 ViT 里的 patchify 操作:输入时,对图像做步长为 $p$ 、卷积核大小 $p \times p$ 的卷积,即把每 $p \times p$ 个像素过一个线性层压缩成一个 token (这里的 $p$ 被称为 patch size)。在输出时,用一个线性层让每个 token 的输出通道数为 $p \times p \times 3$,再把一个 token 还原成 $p\times p$ 个像素。这个操作是否可行呢?
DiT 论文发现,当参数 $p >= 4$ 后,DiT 生成质量会出现明显下降。因此,自 DiT 之后,所有的大型扩散模型几乎都将 $p=2$ 作为默认设置。
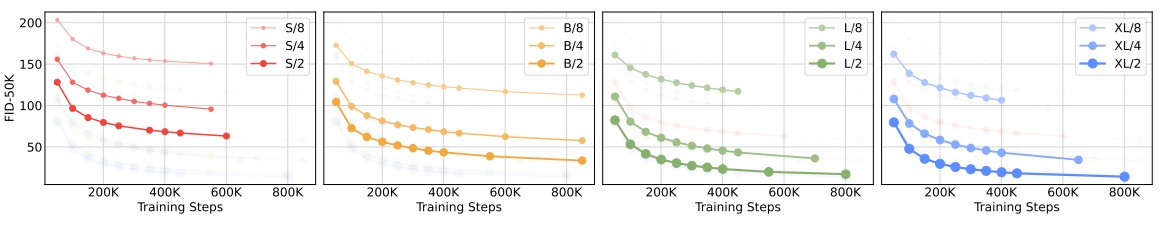
然而,仅将输入序列压缩 $2\times 2$ 倍,高分辨率像素图像的元素数还是太多了,DiT 的运算速度会非常慢。此前尝试在像素空间训练 DiT 的文章有 PixelFlow 和 PixelNerd。PixelFlow 照搬了 f-DM,PyramidFlow 的多阶段加噪方式,让扩散模型在生成时从低分辨率图像开始,一边去噪,一边做上采样。基于这一设计,PixelFlow 成功训练了一个 $p=4$ 的 DiT。PixelNerd 则认为,patchify 对输入的处理没问题,但将 token 还原成 pixel 的过程可以优化。因此,PixelNerd 用了一个类 Nerf 的网络来解码像素值,而 DiT 仅作为一个 encoder。最终 PixelNerd 训练出了一个 $p=16$ 的 DiT。
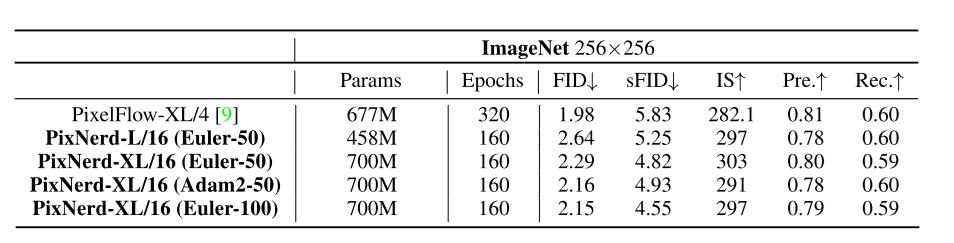
这两个工作都对原来的 DiT 做了不少改进。能不能进一步简化,直接在 ImageNet-256 上训练一个 $p=16$ 的普通 DiT 呢?这就是 JiT 要解决的问题。
Pixel DiT 动机总结
早期像素空间的 ADM 效果不够理想。LDM 通过加入潜空间来提升训练效率与生成质量,但它只是绕过而不是解决了长序列生成问题。ADM 的改进方向有两个:1)改进长序列下的加噪方法;2)从 U-Net 升级成 DiT。前者已经被成熟研究并广泛用于当前的大型扩散模型了。而 Pixel DiT 的研究还不够多,其瓶颈在于 patch size 过大时 DiT 生成质量会严重下降,必须加入一些额外的设计。而 JiT 试图训练一个不带任何额外设计,且 patch size 较大的 pixel DiT。
扩散模型预测目标
JiT 做的事情可以用一句话概括:把 DiT 的预测目标从 $v$ 换成 $x$。熟悉扩散模型的研究者可能一眼就能看懂这句话是什么意思。当然,为了让人人都能看懂,在这一章里,我们将在如今最常用的 rectified flow 噪声调度器下,回顾扩散模型的三种预测目标及其相互转换方式。
目前最常用的 rectified flow 加噪公式为
其中,$x$ 是清晰图像,$\epsilon$ 是高斯噪声,$z_t$ 是 $t$ 时刻的带噪图像。注意,和早期的 DDPM 相反,这里时刻 0 时图像为纯噪声,时刻 1 时图像为清晰图像。而早期我们用 $x_t$ 来称呼带噪图像,并用 $x_0$ 指代清晰图像。这个公式非常简单,就是清晰图像和噪声之间的线性插值。

为了方便理解,我们将所有图像画成一维数轴上的点。但实际上它们是在高维空间里的。扩散模型的学习目标可以简单解释为:我们现在有一个高维空间里的点 $z_t$,该怎么找到终点 $x=z_1$ 呢?
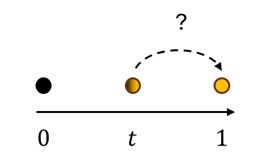
扩散模型的神经网络主要有三种预测目标:噪声 $\epsilon = z_0$,清晰图像 $x = z_1$,以及两者之间的速度 $v = x - \epsilon$。因为两点确定一条直线,而我们又知道了当前点在哪,所以只需要再知道直线上的一个量,就知道了直线的所有信息。以论文中用到的方法为例,我们来看已知 $z_t, x$ 时该如何求 $v$。
已知 $z_t, x$,我们就能求出它们之间的位移 $v’=x-z_t$,并知道该向量的模长为 $1-t$。而 $v$ 的方向相同,模长为 $1$。因此,我们可以求出 $v=(x-z_t)/(1-t)$。

JiT 方法实现
尽管我们知道扩散模型的三种预测目标之间可以转换,但神经网络学习预测三种目标的难度是不同的。JiT 认为,在设计预测目标时,有两个设计空间:1)让神经网络输出哪个预测目标;2)让哪个预测目标求 l2 loss。由于网络输出的目标之间可以互相转换,所以第一步和第二步可以用不同的预测目标。还是拿刚刚的例子,假设我们预测 $x_\theta$,但是要用 $v_\theta$ 求 loss,我们就先让网络输出 $x_\theta = \text{net}(z_t, t)$,用 $v_\theta=(x_\theta-z_t)/(1-t)$ 求出预测的速度,再对 $v_\theta$ 和 $v$ 求 loss。
如下面的消融实验结果所示,预测 x,使用 v-loss 是最优的。
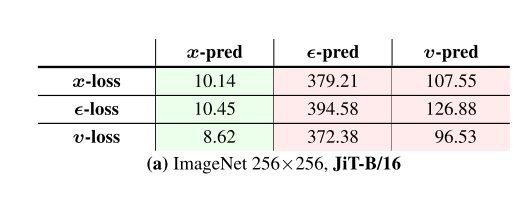
JiT 的主要改动就是以清晰图像为预测目标,其他改动的影响相对没那么大。我简单列举一下其他的改动。
噪声强度偏移。如前文所述,对高分辨率图像得加更多的噪声。JiT 使用了 SD3 的 logit-normal t 采样技术。这一改动也能大大降低 FID 指标。
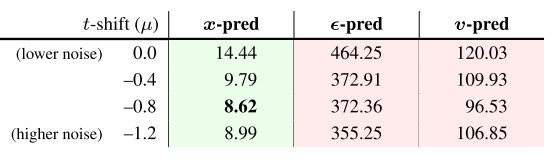
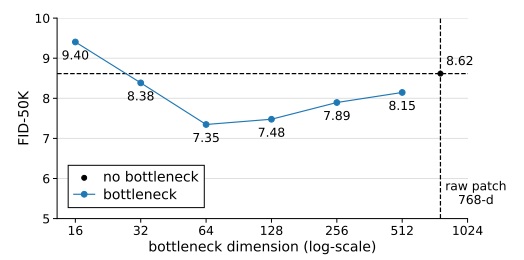
Bottleneck 嵌入层。原来 DiT 在将输入通道数变成模型通道数时,只会用一个普通的线性层。而 JiT 把它换成了一个双层 bottleneck 结构:先降维,再升维到模型通道数。这个模型设计上的小改动也能提升生成质量。
现代 DiT 结构。JiT 参考之前的 LightningDiT (即提出了 VAVAE 的论文),对 DiT 的模块进行了改进,使用了 SwiGLU, RMSNorm,并将位置编码换成了 RoPE,还加入了 qk-norm。
针对 class condition 的优化。 JiT 参考同组工作 MAR,将单个类别 token 拓展成了 32 个类别 token。此外,JiT 还用了一种叫做 CFG interval 的技术,能够提升 CFG 的采样质量。

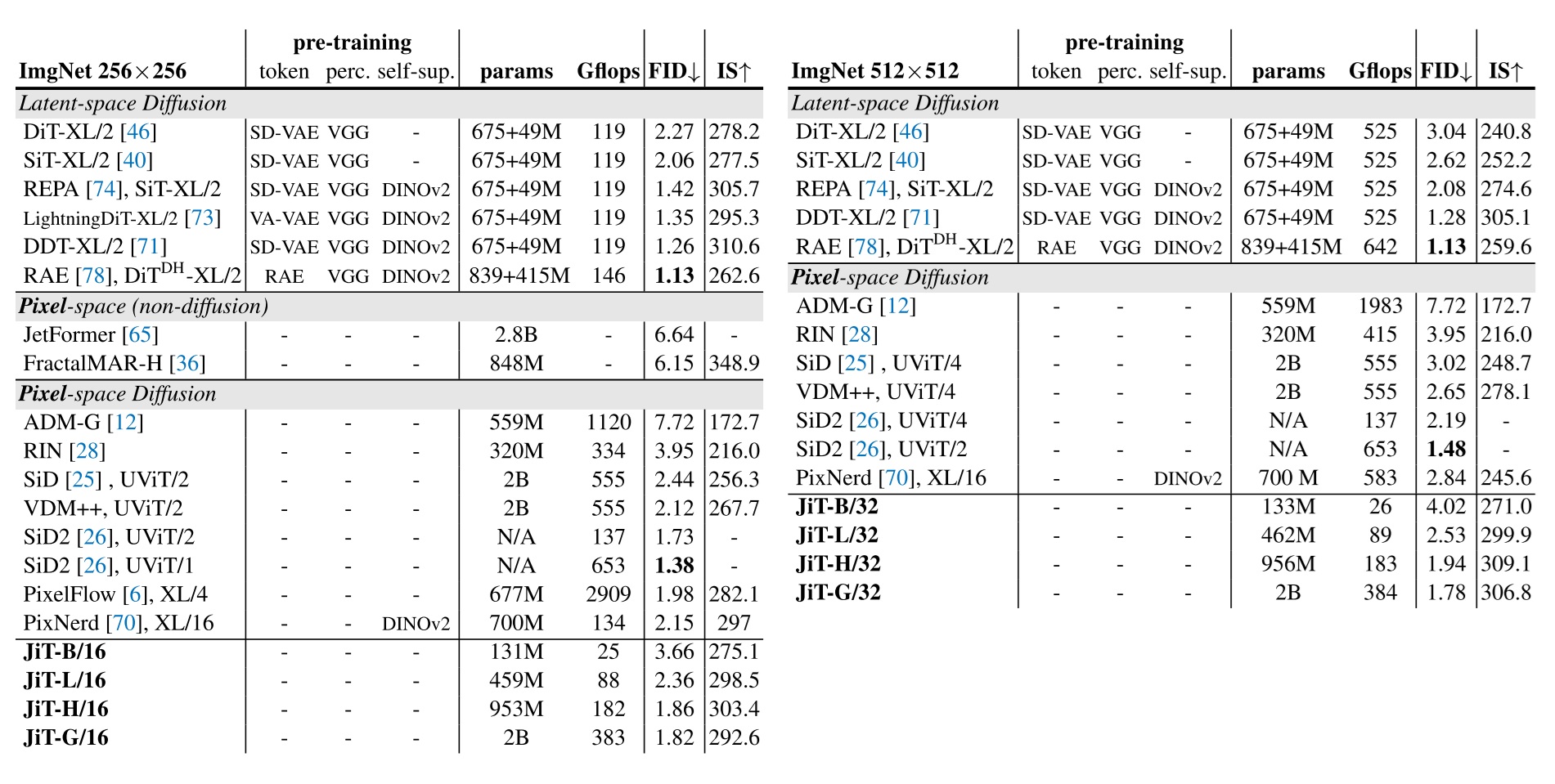
最终训练出来的 JiT 在 ImageNet-256, ImageNet-512 上都取得了不错的结果。
实验分享
到目前为止,我仅仅是重述了 JiT 论文的内容,并没有对其内容做进一步分析。在这一章,我会分享我复现论文时一些有趣的经历,并基于我的实验结果进行分析。
代码实现
在我的训练环境里,我已经准备好了 FFHQ-128 数据集及一个加入了 RoPE 的流匹配版 DiT。我想快速验证一下预测清晰图像这件事能带来多大的提升。恰好,JiT 论文正文给出了 Python 风格的伪代码简明实现,我就直接把它搬进我的代码了。如果已经准备好了 v-prediciton 的训练环境,只需要按照下图红框所示,稍微改几行代码,就能预测清晰图像并启用 v loss 了。

改完之后,我碰到的第一个问题是 loss 出现 NaN。我敢保证这个代码库没有问题,那么出问题的应该是数据范围。我仔细审视了被改动的代码,发现将 x-prediction 转成 v-prediction 时,会出现 / (1-t) 这个操作。假设取 1000 个扩散模型训练步数,那么 t 的范围是 [1/1000, 1]。这就会让某些 t 的 loss 出现乘 1000 倍的操作,进而导致数值爆炸,出现 NaN。
经验告诉我,应该像梯度裁剪一样,把这个权重设一个上限才行。我只好去翻看了 JiT 的 PyTorch 官方实现代码,果然看到了下面的操作:
1 | /(1-t).clamp_min(5e-2) |
也就是说,分母最小是 5e-2,乘的权重最大是 20,这样梯度不会炸掉。关于这样改动的合理性及其背后的影响,我会在后文分析。
改完这个 bug 后,模型总算训起来了。但是,模型在采样时永远只能生成纯黑的图片。这又是哪错了呢?为了确保论文里的速度和我代码库的速度的定义一致,我自己推导了一遍 x 和 v 的转化公式。最后发现,速度的定义没错,论文里 t 的定义和我这里是反过来的!我用的 Diffusers 库坚守 DDPM 的老传统,把 t=0 当成清晰图像,t=1 当成纯噪声。不知道哪个发明流匹配的人硬生生把这个定义反了过来。太烦人了!
改完这两个 bug,模型总算是成功训出来了。
实验结果分析
实验结果显示,x-prediction 比我之前用的 v-prediction 差得多得多!这是论文有问题吗?我只好回头认真阅读了几遍论文。我在粗略地看了一遍论文后,认为论文的主要主张是「高分辨率像素 DiT 用 x-prediciton 更优」。于是,我在 $128\times128$ FFHQ 数据集上训练了一个 p=1 的 DiT-S 。既然没有复现出论文的结果,那多半是我的配置有点问题。比对过后,我发现我配置上的主要区别是 p。按照论文里将输入序列缩减到 $16 \times 16$ 的做法,我在边长 128 的数据上采用了 p=8 的配置。这下总算复现出了论文的结果。
如下图所示,_base 指的是用 v-predition 的 baseline,_x0 指的是 JiT 最终采用的 x-prediction + v loss。我这里输出的是 1000 个样本的 FID 指标 (越低越好)。训练一共执行 200 个 epoch,batch size 为 256。
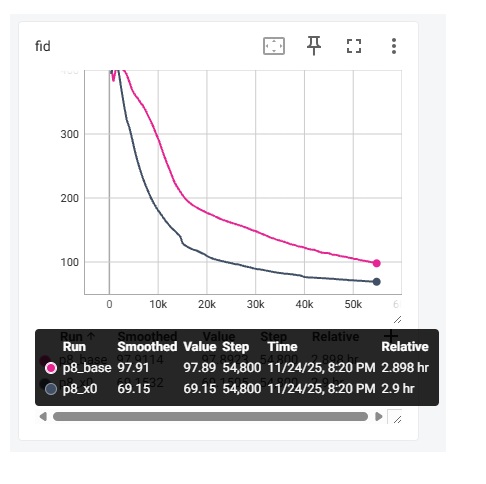
这样看来,我对论文的结论理解似乎有误。论文的真正结论应该是「大 patch size 的 DiT 用 x-prediciton 更优」,和分辨率究竟多大,以及是否是像素 DiT 无关。
为了进一步验证我的结论,我做了 p = [1,2, 4, 8] 在 baseline 和 JiT 配置下的 8 个实验。各个实验的 Batch Size 及训练量如下所示:
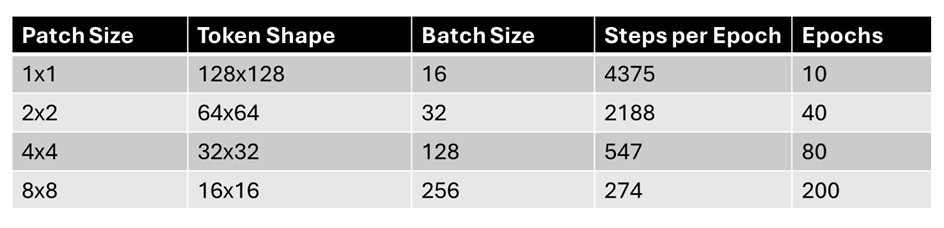
首先,我们先来复现一下 DiT 的结论:p=2 时,模型的质量尚可接受。再增加 p 则会大大降低模型质量。相关的图表如下所示。(由于我在 p=2,4 时训练了两个阶段,图表会比较杂乱,还望见谅)
先看一下 p=1,2 时的对比。从曲线上看,二者几乎是重合的。但由于 p=2 时 batch size 是 p=1 时的两倍,所以训练的数据量相同时,p=1 还是最优的。我之前有一个训了更久的 p=1 的模型,FID 差不多就是 43 左右,而图中训了 40 个 epochs 的 p=2 模型 FID 为 43.94。也就是说,充分收敛时,p=2 确实不太会影响生成质量。

再增加 patch size 的话,情况就不一样了。p=4 训 80 个 epochs 还比不过 p=2 训 20 个 epochs 的质量。而 p=8 时,几乎看不到能收敛的希望。

接着,我们来对比 baseline 的 v-prediciton 和 JiT 的 x-prediction + v-loss。仅在 p=8 时,JiT 比 baseline 更优。在 p 更小时,还是 baseline 更优。而且,在 p=8 时,x-prediction 也挽救不了大 patch size 带来的质量下降。哪怕它训练了 200 个 epochs,最终的 60 多的 FID 也比不过小 patch size 下训练 epoch 数更少的模型。
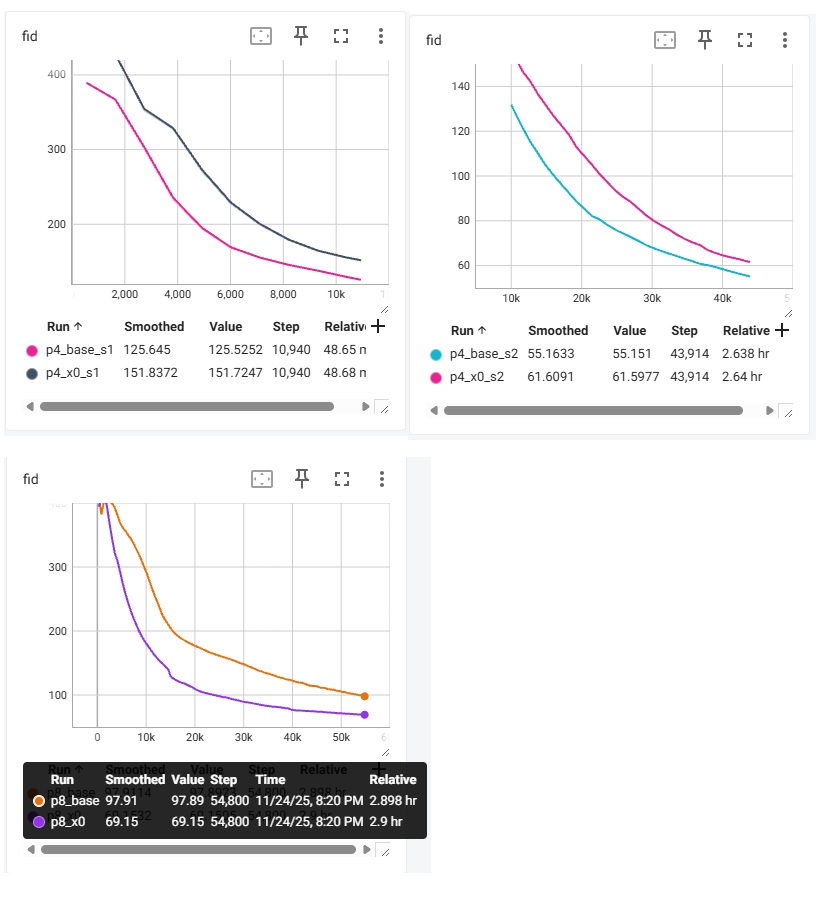
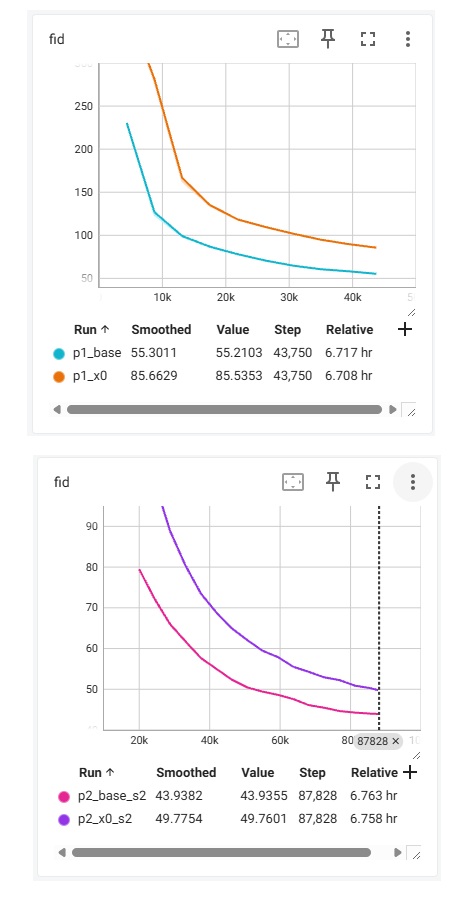
通过这些实验,我可以断言,JIT 提出的扩散模型预测目标仅在大 patch size 下有效。这个方法仅仅是不得不用大 patch size 时的无奈之举。如果计算资源足够,用原来 v-prediction 的小 patch size 模型还是更好的。
解释实验结果
流形假设基础
为什么 JiT 在大 patch size 时有效呢?JiT 论文用流形假设 (manifold assumption) 理论来解释这个现象。在探讨 JiT 为什么有效前,我们先简单认识一下流形假设。由于我也没有系统学习过这个概念,只能用一些不太严谨但非常直观的例子来解释它。
流形假设表示,高维空间的数据集里的数据并不是均匀分布在整个空间里,而是在一个低维流形上。我们可以用一个简单的例子来说明:假设我们有一个灰度值构成的数据集,可能的灰度值是 [0, 255]。但是,我们存储这些颜色的数据集用的是 3 通道的 RGB 颜色。虽然 RGB 颜色空间有 $256^3$ 种可能,但实际上灰度值只有 $256^1$ 种,且它们分布在一条直线上。这条直线就是高维 3D 空间里的 1D 流形。
JiT 还提出了另一个命题:符合流形假设的数据更容易被神经网络预测。而在扩散模型的预测目标中,纯噪声 $\epsilon$ 是不符合流形假设的,因为它均匀分布在整个高维空间。因此,由纯噪声算得的 $v$ 也是不符合流形假设的。只有来自真实数据集的清晰图片符合流形假设。
为了验证该命题,JiT 开展了一个迷你实验:为了构造出符合流形假设的数据集,作者将一个 2D 图形用一个维度为 D 的随机投影矩阵投影到了 D 维。接着,作者训练了三个预测目标不同的扩散模型,观察哪个模型能够成功预测这个投影后的 D 维数据。结果发现,随着 D 增加,只有 x-prediction 维持不错的预测效果,预测 $\epsilon$ 和 $v$ 都不行。
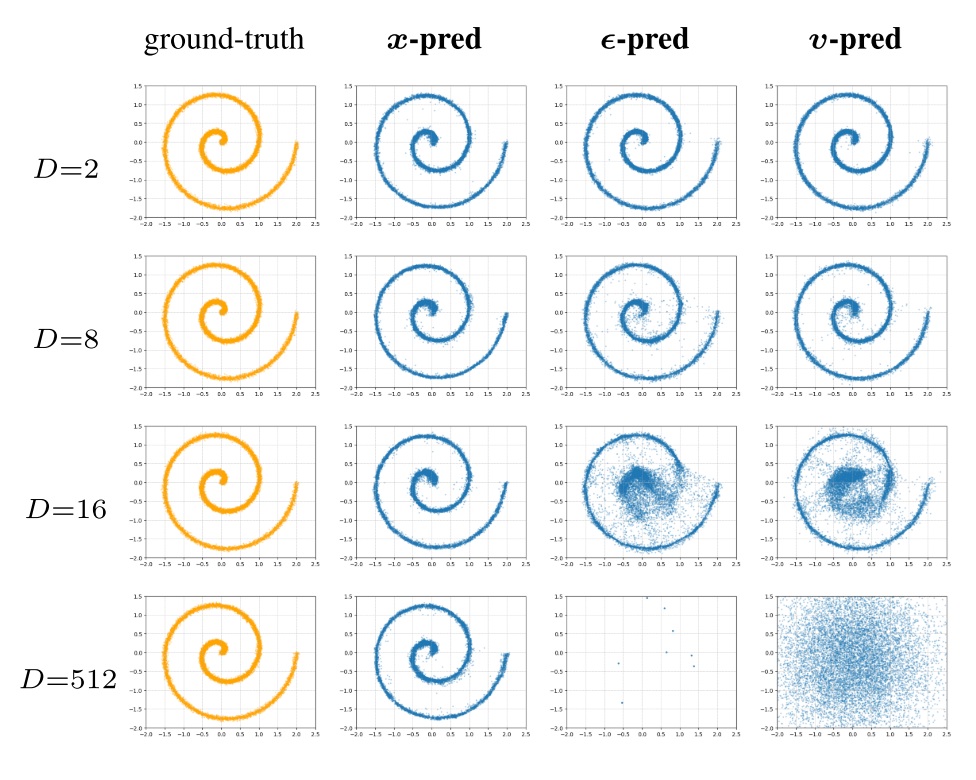
这个实验证明,我们对神经网络拟合能力的理解是正确的:神经网络更擅长拟合符合流形假设的数据集。
大 patch 与流形假设
如果神经网络与流形假设的理论是对的,那么 x-prediction 应该总是更优的,为什么我们在 JiT 中发现只有大 patch size 时更优呢?作者在论文里没有详细讨论这一点,而我通过之前的知识大概想出了原因。这涉及神经网络的更底层的概念:一个 Transformer 到底预测了什么?
在学习神经网络的时候,我们会先学全连接网络,再学 CNN, RNN, Transformer。一般教程会说,全连接网络更容易过拟合,而其他网络泛化性更好。但仔细思考后,我们可以更具体地指出全连接网络和其他高级网络的区别:全连接网络用一套参数建模了所有输入到所有输出的关系,换句话说,对于每个输出元素,它用到的参数是不同的。而其他高级网络实际上是在用同一组参数输出一个元素,只不过输出某元素时,输入还包含其它元素的信息。
以 CNN 和 Transformer 为例,我们来验证这个概念。CNN 对每个元素都用同样的卷积核,只不过每个卷积核的输入不同;Transformer 的注意力操作是一个无参数的信息融合操作,其他所有投影层、MLP 全是逐元素生效的。
神经网络其实只负责输出一个数据元素,而现在的扩散模型 loss 或者交叉熵 loss 都是逐元素计算的。所以,看上去神经网络学习的是整个数据集的分布,但它只需要学到整个联合分布的分解 (factorization),也就是其中某一项数据的规律即可。
根据这个假设,我们来尝试解释 patch size 对 DiT 的影响。不加 patch size 时,图像的每个数据元素是一个三通道的像素。单个像素的分布可能非常容易学,不管它是清晰图片,还是由纯噪声计算出的速度。这时,是否符合流形假设不影响学习难度,因为数据本身的维度就低。哪种预测方式更好需要用另外的理论解释。
而增加 patch size,其实是让单个元素的分布更加复杂了。我们可以忽略 patchify 里的线性层,把 patchify 看成是把 $p \times p$ 个像素在特征维度上拼接,把三通道数据变成 $3pp$ 通道的数据(事实上,FLUX.1 的 patchify 就是这么做的)。这个通道数为 $3pp$ 的数据才是真正的「高维数据」,Transformer 要预测的输出通道数是 $3pp$。这时,就可以根据前面迷你实验的结论,用流形假设来解释为什么 $p$ 较大时 x-prediction 更好。
x-loss 和 v-loss
正如 JiT 论文所说,扩散模型的预测目标和求 loss 的目标是解耦的。论文表格显示,v-loss 总是好于 x-loss。这里我将针对 JiT 的代码实现来简单讲一下解释该现象的思考方向。
在代码中,如果要用 x-prediction + x-loss,会这样写:
1 | input x |
如果换成 v-loss,会改成这样:
1 | input x, eps, t |
观察两组 loss,我们发现,其实 v-loss 里那个减去 z 是没用的,因为不管的预测值还是 GT 都带了 -z。因此,x-loss 和 v-loss 的唯一区别就是后面的 /(1-t)。越是靠近清晰图像,1-t 越靠近 0,loss 权重更高;反之,越靠近噪声,loss 权重越低。所以,不同的 loss 其实就是在不同的 t 时用了不同的权重而已。哪种 loss 最优很难用理论解释,现在大家都是从调参实验中获取结论。
我们再来讨论一下代码里为什么可以对分母加 .clamp_min(5e-2)。训练时每个 t 的权重不影响训练的正确性,为了数值稳定,加这个没问题。但采样时,如果算速度时还加了这个,按理来说采样算法是错误的。但换算过来,只有 t < 0.05 时采样公式才不对。如果采样总步数是 50,只有最后两步是不对的。可能这个微小的误差对于采样算法来说是可以接受的吧。
总结
此前大家没能成功训练出 ImageNet-256 上 p=16 的 DiT。JiT 用 x-prediction 取代 v-prediction 解决了此问题。这一做法背后的理论基础是流形假设和神经网络的 factorization: 神经网络将预测复杂分布分解成了预测每一个简单元素的分布,而 patchify 把原本低维的元素变成了高维的元素。此时,如果在预测目标中加入噪声,就会违反流形假设,让模型要学习的高维数据分布过于复杂。
虽然论文最终也把 JiT 在 ImageNet-256 的 FID 训到了 2 以下,比 DiT 要好,但 JiT 用了更多训练和采样的 trick,完全相同的环境下不见得能比得过 VAE + patch size=2 的 DiT。在我自己的实验里也发现,patch size 较小的 v-prediction 仍然是最好的。正如作者在 conclusion 中所写,JiT 的意义可能是用于 tokenizer (或者说压缩数据的 VAE) 不好获取的场合,这时我们能够用大 patch size 直接对输入数据做压缩。另外,我认为 JiT 做的高分辨率像素图片生成和隐空间图片生成没啥区别。隐空间图片分辨率上去了,一样会面临难以训练的问题。因此,JiT 的贡献或许和是否有隐空间无关,它是一种适用于任何数据的,提升大 patch size DiT 生成质量的方法。
就论文写作上,我认为作者虽然写了一套看起来很有逻辑的故事,但没有把核心贡献讲清楚,而仅仅是在方法部分分析了 pathchify 过后维度变大导致了数据不符合流形假设。如果不是亲手做实验,我根本想不到 x-prediction 有效的场景不是 「高分辨率像素图像生成」,而是「大 patch size DiT 生成」。为了让读者能够更好理解论文,作者最好能在 introduction 里花更多的文字讲清楚是 patchify 导致了高维数据的产生,再讲高维数据与流形假设的关系。论文也最好能够提供本文所展示的同一分辨率不同 patch size 下模型的生成质量,以清楚地说明 patch size 决定了 x-prediction 是否有用。当然,我认为文章提出流形假设这个理论还是很有启发性的。此前我从来没有仔细想过为什么 patchify 会让 DiT 变得难训,但把它和流形假设以及神经网络的逐元素预测结合起来后,一切就清晰起来了。
看完这篇论文后,我的第一感是,patchify 对于输入的处理没有问题,但是在输出阶段还原数据尺寸时的做法过于简单。那么,是不是可以用另一个网络来专门负责解码像素级输出,而大 patch size 的 Transformer 仅作为编码器?比如再用一个像素 Transformer,但是注意力层只看自己的像素级特征和之前的 patch 级特征。这个 idea 或许很常见,之前隐空间里的 DDT 、像素空间的 PixelNerd 都用了类似的做法。但没想到,就在前两天,陆陆续续有好几篇像素空间 DiT 生成工作发表了出来,做法跟我这个想法都差不多。看来像素 DiT 这个领域能做的空间也越来越少了。
个人感想
最后谈一点和本文不是很相关的感想。一直以来,我觉得多数人对于扩散模型的学习方式存在误区,好像弄完一堆数学推导,知道 DDPM 和 Flow Matching 是怎么建模的才是最重要、最高大上的。但实际上,除非是专门做与理论紧密相关的研究,比如采样加速,否则理解这些公式对调优扩散模型的结果毫无帮助。从本文的结果也能看出,仅用数学理论完全无法解释要用哪种 loss,以及为什么如何不同 t 时设置不同的权重。究竟怎样的噪声公式最好,其实取决于神经网络的性质以及常见数据集的分布规律,而和预定义的扩散模型公式无关。是扩散模型公式去适应神经网络,而不是让神经网络预测某个预定义的公式变量。所以,在研究扩散模型或者其他生成方法时,必须要像物理一样从现象中归纳,而不是像数学一样基于演绎推理。而且,研究过程中也必须涉及对神经网络的分析。现在 AI 的发展很多都是经验、实验指导的,但要长期发展的话,必须建立某种理论模型,不论这个模型是否与传统的数学模型相容。
参考文献
(JiT) Back to Basics: Let Denoising Generative Models Denoise
(ADM) Diffusion Models Beat GANs on Image Synthesis
(VQVAE) Neural Discrete Representation Learning
(VQGAN) Taming Transformers for High-Resolution Image Synthesis
(LDM, Stable Diffusion) High-Resolution Image Synthesis with Latent Diffusion Models
(ViT) An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
(DiT) Scalable Diffusion Models with Transformers
(Stable Diffusion 3) Scaling Rectified Flow Transformers for High-Resolution Image Synthesis
(SD) simple diffusion: End-to-end diffusion for high resolution images
(SiD2) Simpler Diffusion (SiD2): 1.5 FID on ImageNet512 with pixel-space diffusion
(Diffusion Noise SNR 研究) On the Importance of Noise Scheduling for Diffusion Models
(f-DM) f-DM: A Multi-stage Diffusion Model via Progressive Signal Transformation
(PyramidFlow) PyramidFlow: High-Resolution Defect Contrastive Localization using Pyramid Normalizing Flow
(PixelFlow) PixelFlow: Pixel-Space Generative Models with Flow
(PixelNerd) PixNerd: Pixel Neural Field Diffusion
(VAVAE, LightningDiT) Reconstruction vs. Generation: Taming Optimization Dilemma in Latent Diffusion Models
(MAR) Autoregressive Image Generation without Vector Quantization
最新 Pixel DiT 论文 (除此之外,JiT 表格里对比的所有 baseline 论文都值得阅读):
Advancing End-to-End Pixel Space Generative Modeling via Self-supervised Pre-training
DiP: Taming Diffusion Models in Pixel Space
DeCo: Frequency-Decoupled Pixel Diffusion for End-to-End Image Generation
PixelDiT: Pixel Diffusion Transformers for Image Generation