作者亲述 | Log-linear Sparse Attention:首个 $O(N \log N)$ 高性能稀疏注意力
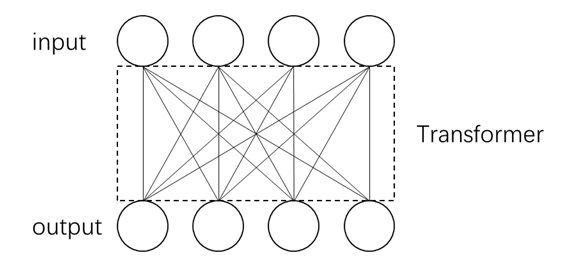
$O(N^2)$ 复杂度的自注意力操作一直是当前大模型的计算瓶颈。今年,注意力的一个热门改进方向是稀疏注意力:不对所有 KV token 求注意力,只对极少数重要的 KV token 求注意力。这个方向的代表作是 Kimi 的 MoBA 和 DeepSeek 的 NSA。然而,这些稀疏注意力并没有真正降低该运算的复杂度,总运行时间仍随着序列长度 $N$ 按照 $O(N^2)$ 的趋势增长。
针对这一问题,我们团队近期的研究 Log-linear Sparse Attention (LLSA) 从算法设计的层面将以往稀疏注意力的复杂度优化至 $O(N \log N)$。同时,我们用 Triton 编写了一套适配当前 GPU 架构的 LLSA 的高效并行实现,并用较优的稀疏算法尽可能减少了稀疏操作的时间占用。我们在无 VAE,无 Patchification 的纯像素 DiT 生成任务上验证了 LLSA 的有效性。在最长为 $512 \times 512$ 的像素序列上,LLSA 的生成质量不逊于全注意力,而运算时间大大缩短。
在这篇博文中,我会介绍我们团队在 arXiv 上发布的 Trainable Log-linear Sparse Attention for Efficient Diffusion Transformers 论文,并在文末给出我对论文的评价并探讨论文未来拓展方向。LLSA 的高性能 Triton 实现也已经开源。欢迎各位科研同行使用我们的方法,或是在读完论文后与我们交流、合作。
arXiv: https://arxiv.org/abs/2512.16615
GitHub: https://github.com/SingleZombie/LLSA

背景介绍
首先,先明确一下 LLSA 的适用范围。正如论文标题所写,这是一种可训练的 (trainable) 注意力机制。因此,它和 Sparse VideoGen 等面向预训练模型推理加速的方法不同,不必保证输出和全注意力尽可能接近,只要能训练一个带有这种注意力的 Transformer 就行。LLSA 对标的是 MoBA (Mixture of Block Attention), NSA (Native Sparse Attention) 这样的注意力机制,拥有更大的设计空间。
在这一节中,我将先补充背景介绍,帮助读者理解我们在解决一个怎么样的问题。之后,我会简单回顾一下和这个工作相关的早期工作。
注意力的稀疏化
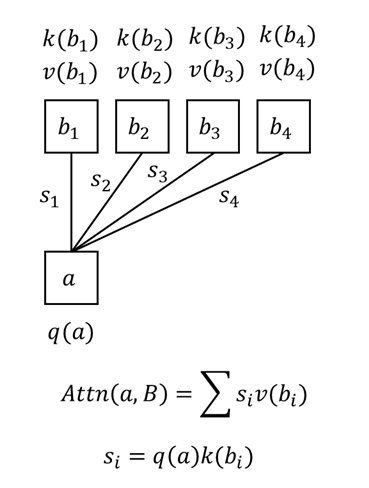
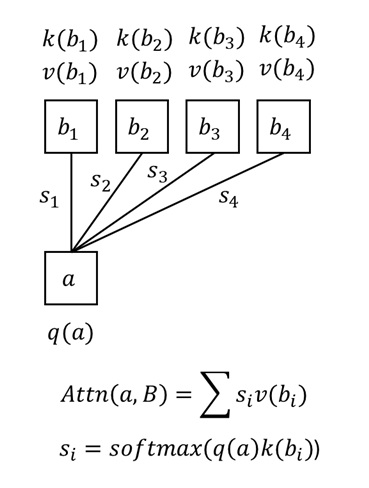
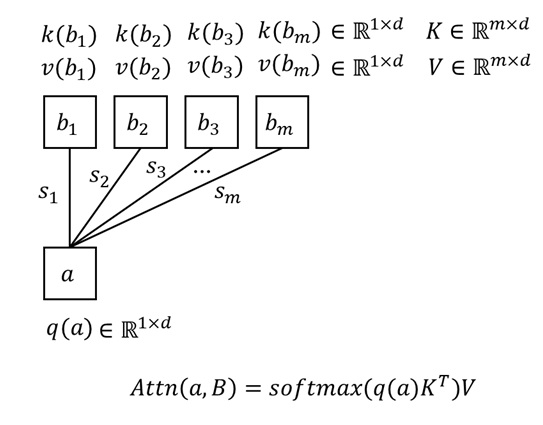
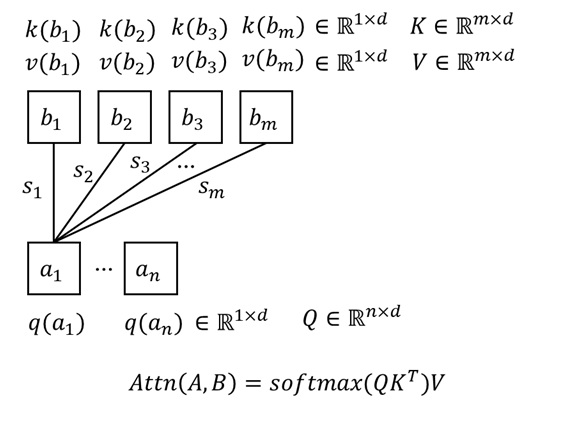
注意力操作可以简单表示为:
其中,$\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N\times d}$,$N$ 是序列长度,$d$ 是特征通道数。我们通常将 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ 称为 query, key, value。
上面的公式其实是 $N$ 个 query 合并成矩阵的写法。如果一次只考虑一个 $q \in \mathbb{R}^{1\times d}$ 的话,注意力公式会更容易理解。我们先算一个 query 对所有 key 的归一化相似度 $p = \text{softmax}(q \mathbf{K}^{\intercal})$,再把这个相似度用逐元素乘法乘到 value 上,得到该 query 的注意力输出 $o = p\mathbf{V}$。把所有 $o$ 拼接成矩阵就得到了最后的输出 $\mathbf{O}$。
理解了注意力公式后,我们来从复杂度的角度讨论为什么标准全注意力那么慢。因为有 $N$ 个 query,每个 query 要对 $N$ 个 key, value 求注意力输出,所以总复杂度是 $O(N^2)$。或者我们可以直接考查矩阵乘法 $\mathbf{Q} \mathbf{K}^{\intercal}$,由于 $\mathbf{Q}, \mathbf{K}\in \mathbb{R}^{N\times d}$,该矩阵乘法的复杂度是 $O(N^2d)$,忽略通常为常数的 $d$ 后复杂度是 $O(N^2)$。由于时间复杂度为序列长度的平方,所以在 Transformer 序列长度逐渐变长后,我们会发现注意力操作的速度下降得极快,相比其他线性复杂度的计算 (MLP, Norm),时间占比越来越高。
而许多研究表明,其实预训练模型里的注意力矩阵 $\mathbf{P} = \text{softmax}(\mathbf{Q} \mathbf{K}^{\intercal})$ 都是稀疏的。或者更具体地说,对于每个 query,大多数 key 的相似度都接近 0,忽略掉这些 key 也没关系。根据这个观察,一个很自然的想法是:能否使用 Top-$K$ 算法,每次只取最重要的 $K$ 个 key, value,而跳过其余的呢?
这个想法从正确性上来看并没有问题。但仔细一想,这个想法好像并不能实现加速:为了求 Top-$K$,我都把 $O(N^2)$ 个 query, key 相似度算完了,那还用稀疏注意力干什么呢?直接把 value 再乘上不就算完了?所以,这里的问题是:如果不能高效地算出 query, key 相似度,那么 Top-$K$ 稀疏注意力并不能实现加速。
现在我们常见的 Top-$K$ 稀疏注意力其实用了一个更高效的算法粗略算出了 query, key 的相似度。在认识它之前,我们先回顾一项前置知识:Block Sparse FlashAttention。
Block Sparse FlashAttention
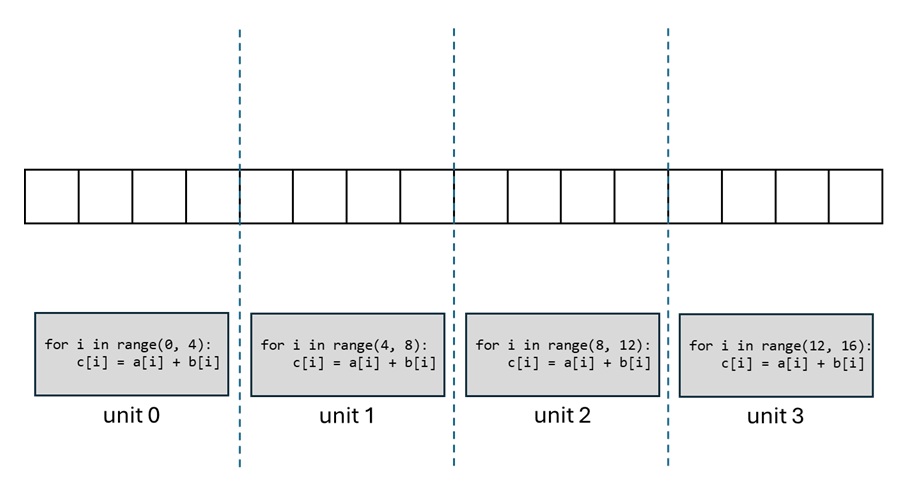
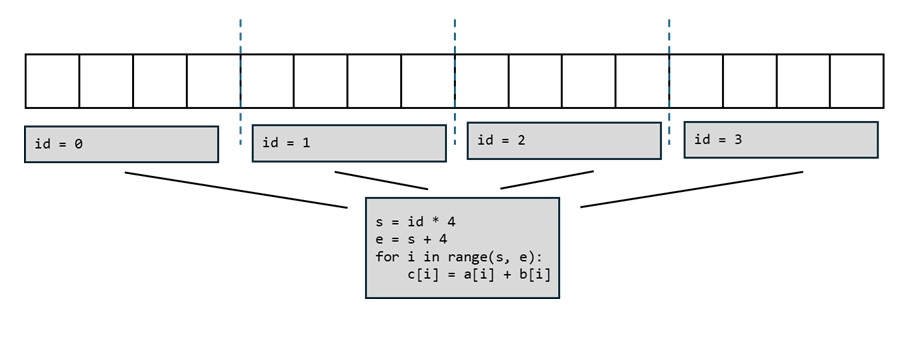
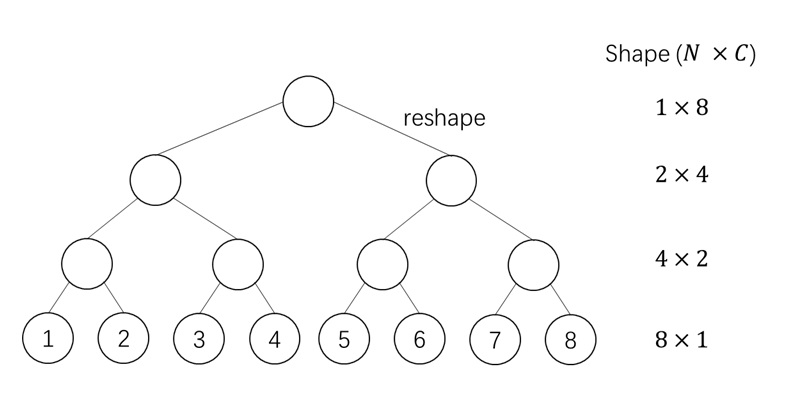
现代 GPU 编程都基于并行计算:GPU 可以同时算 $B$ 个同类型的计算。所以,假设我们要对两个长度为 $N$ 的向量求和,我们不是写一个长度为 $N$ 的循环,每次算一个元素,而是写一个长度为 $N/B$ 的循环(假设可以整除),每次算 $B$ 个元素。
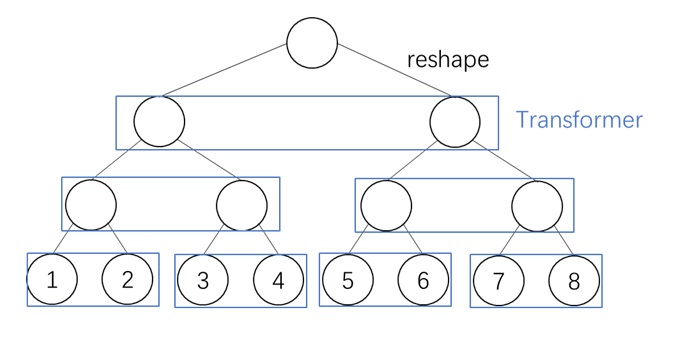
按照这个思想,FlashAttention 实现了一个高效的分块(block)计算。我们假设 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ 被分成了 $N/B$ 组,第 $i$ 组的 token 满足 $\mathbf{Q}_i, \mathbf{K}_i, \mathbf{V}_i \in \mathbb{R}^{B\times d}$。这样我们可以用 $N/B$ 个程序实现注意力运算,每个程序并行计算 $B$ 个 $\mathbf{Q}_i$ 的输出 $\mathbf{O}_i$。同时,在每个程序里,我们使用一个长度为 $N/B$ 的循环,每次处理 $B$ 个 $\mathbf{K}_i, \mathbf{V}_i$。这样的运算方式可以充分利用 GPU 的并行计算能力。
FlashAttention 天生支持块稀疏 (Block Sparse) 算法:假设我们用某个稀疏算法知道 $\mathbf{Q}_i$ 对 $\mathbf{K}_j$ 不用算,我们在第 $i$ 个程序的第 $j$ 轮迭代 (iteration) 时就可以直接跳过。这里稀疏算法的选择没有限制。比如我们可以用滑动窗口注意力,仅让每个 query 看到相邻的几个 key。
对于 FlashAttention 的详细介绍欢迎参考我的往期博文:不会 CUDA 也能轻松看懂的 FlashAttention 教程(算法原理篇)。
Top-$K$ Block Sparse Attention
有了 Block Sparse FlashAttention 的背景知识,一个高效的 Top-$K$ 稀疏注意力算法也就呼之欲出了。我们可以生成少量能够概括一个 block 所有信息的 query, key 特征,再从这些粗糙特征中计算 Top-$K$ 稀疏模式 (sparse pattern)。具体步骤如下:
- 对 $\mathbf{Q}, \mathbf{K}$ 做 $B$ 倍平均池化,得到 $\mathbf{Q’}, \mathbf{K’}\in \mathbb{R}^{T\times d}$。其中,$T=N/B$。
- 对 $\mathbf{Q’}, \mathbf{K’}$ 求内积,再对每个 query 求出内积 Top-$K$ 的 key block 的下标。
- 根据 Top-$K$ 算法得到的稀疏块下标,执行 Block Sparse FlashAttention。
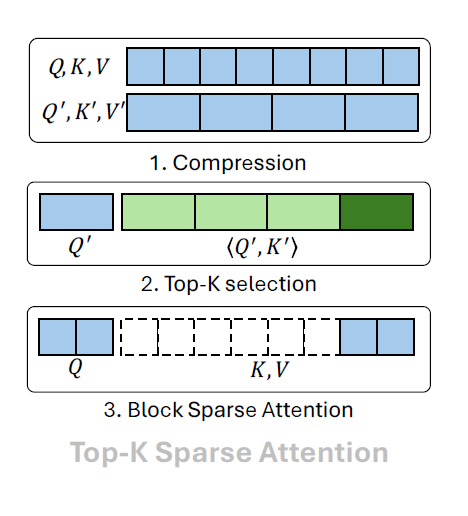
这个稀疏注意力算法可能并不与某个具体算法一模一样,但现在先进的 Top-$K$ 稀疏算法的核心都可以用这个算法表示,比如 MoBA, NSA,以及后文讲到的 VMoBA, VSA, SLA。
我们来粗糙地分析一下这个算法的复杂度。算法的运行时间主要耗费在第二步 Top-$K$ 搜索和第三步注意力计算,我们也只分析这两步。
对于 Top-$K$ 搜索,由于 query block 和 key block 数量都是 $O(N/B)$,所以这一步求内积的复杂度是 $O((N/B)^2)$。
对于稀疏注意力计算,每个 query 能看到 $KB$ 个 key,所以复杂度是 $O(NKB)$。
当 $N$ 不是很大的时候,Top-$K$ 那一步很快,稀疏注意力的运行时间依然占主导。但随着 $N$ 不断增大,含 $O(N^2)$ 那一项迟早会占据主导。也就是说,这种稀疏注意力算法并没有优化全注意力的复杂度,仅仅是让运行速度至多提升了 $B^2$ 倍。而我们的 Log-linear Sparse Attention (LLSA) 的目标是彻底优化掉 $O(N^2)$ 的复杂度。
相关论文
如我们前面反复提及的,NLP 领域使用这种可训练稀疏注意力机制的著名工作是 MoBA 和 NSA。另外,同期学术界也提出了 SpargeAttention,这个稀疏注意力也是基于先平均池化、再过滤的机制,在 NLP 和 CV 领域能够通用。后来 CV 领域提出了 VMoBA,VSA (Video Sparse Attention),SLA (Sparse-Linear Attention) 这三种用于 DiT 训练的稀疏注意力。VMoBA 把 MoBA 适配到了 CV 领域。VSA 和 SLA 都引入了一些机制来解决 Top-$K$ 注意力因稀疏性造成的信息损失问题。VSA 对粗糙 query/key 计算了一个粗糙注意力输出,并将该输出和稀疏注意力输出相加。SLA 用线性注意力高效计算了 Top-$K$ 以外的 key 的注意力输出。
将特征分解成 $O(\log N)$ 层是注意力优化的一种常见思想。比如较早一点的方法有 H-Transformer 和 Fast Multipole Attention。近期比较相关的工作中,Radial Attention 利用一种针对视频的静态稀疏模式,实现了 $O(N \log N)$ 的注意力。而 Log-linear Attention 基于优化线性注意力的质量而非优化全注意力的速度的初衷,使用树状数组为每个 query 维护 $O(\log N)$ 个而不是一个状态。和我们的方法最像的是早期方法 Multi-Resolution Attention (MRA),但这个方法并没有和 FlashAttention 结合,缺乏高效 GPU 实现,也没有在超长序列生成任务上验证。
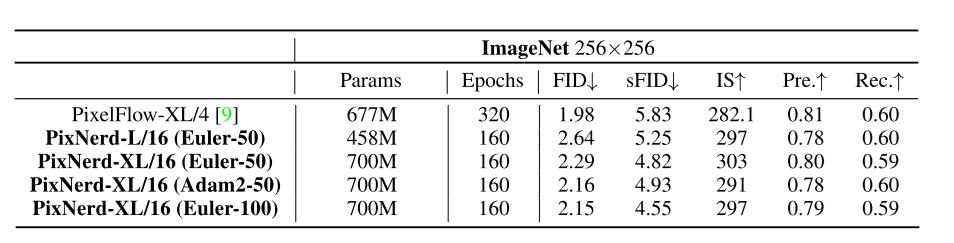
LLSA 以 Pixel DiT 为目标任务。在该科研工作进行时,Pixel DiT 的研究较少,近期工作只有 PixelFlow, PixNerd 两篇。当然,上个月 arXiv 上连续出现了 JiT, DiP, DeCo, PixelDiT 这四篇工作。不过,这些工作虽然没用 VAE,但全部使用了 patchify 压缩 token 数量。没有工作尝试在不用 VAE,不用 patchification 的情况下训练 DiT,因为这种情况下必然要面对注意力计算开销过大的困难。而我们的工作恰好就是冲着这个问题来的,所以最后用高分辨率纯 Pixel DiT 生成任务来验证我们的方法。
Log-linear Sparse Attention 方法实现
下图是论文方法的概览。
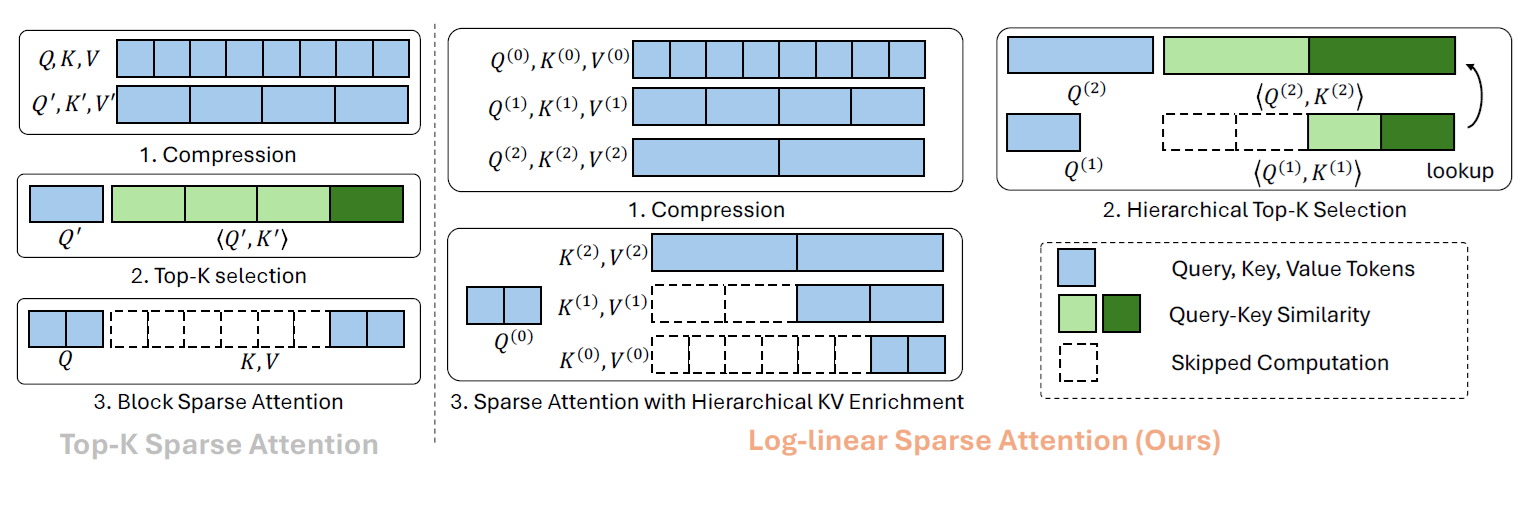
简而言之,LLSA 将以往两级稀疏结构升级成了多层级结构。另外,在最后计算稀疏注意力时,LLSA 不仅用了最精细的 key, value,还用到了不同层级、更加粗糙的 key, value。方法细节介绍如下。
注意力算法
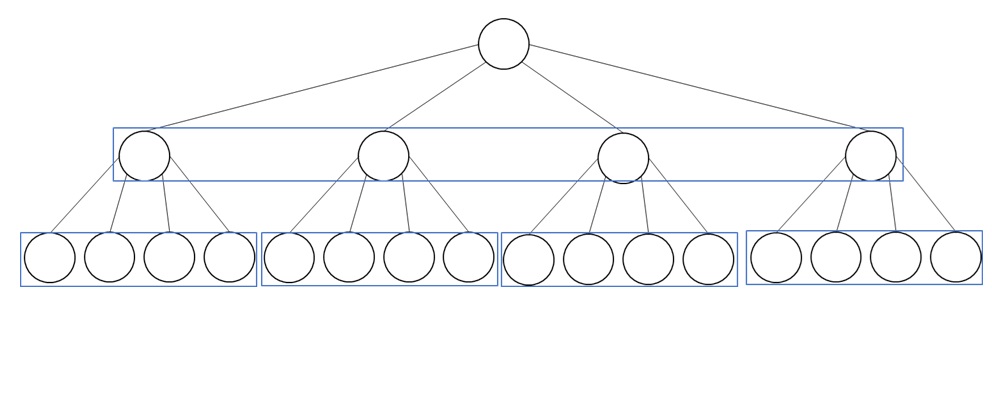
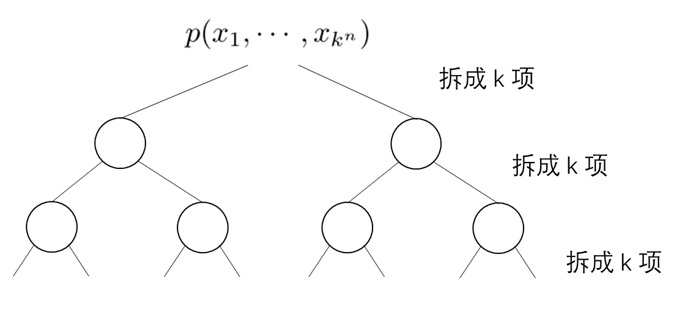
层级压缩。我们把 token 序列按粒度划分成 $L = \log_B N - 1$ 级。为此,我们用 $B$ 倍平均池化逐渐将原 token 特征 $\mathbf{Q}^{(0)}, \mathbf{K}^{(0)}, \mathbf{V}^{(0)} \in \mathbb{R}^{N\times d}$ 压缩成 $L$ 组粗糙 token,第 $l$ 组特征满足 $\mathbf{Q}^{(l)}, \mathbf{K}^{(l)}, \mathbf{V}^{(l)} \in \mathbb{R}^{N/B^l\times d}$。
层级 Top-$K$ 选择。在这一步中,我们自顶向下,由粗到精地为每个 query block 找到 Top-$K$ 相似度的 key block。
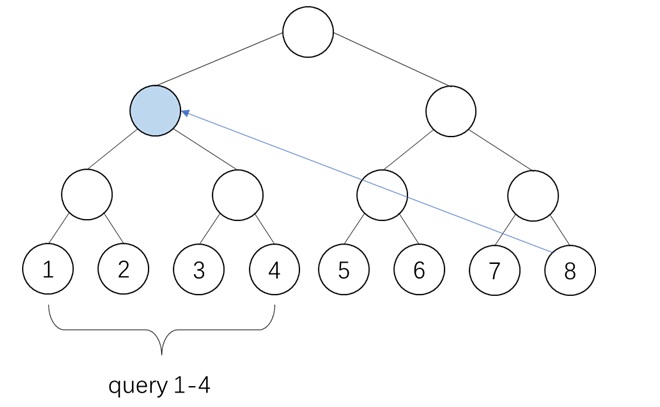
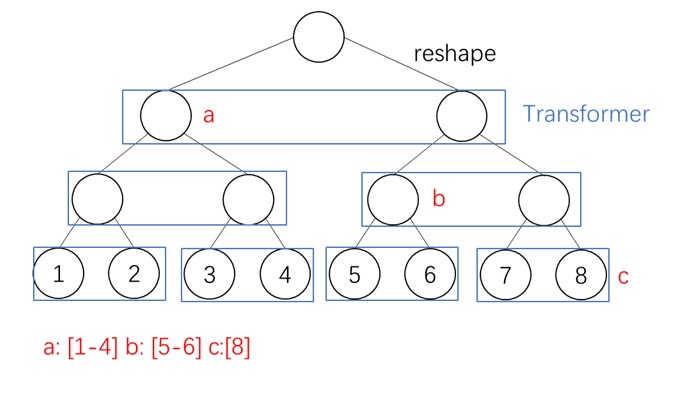
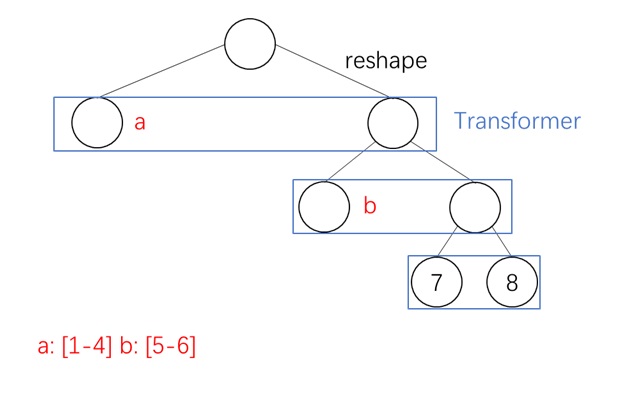
以下面这个 $N=8,B=2,K=1$ 的场景为例。一开始,我们对最顶级(第 $L$ 级)query, key 算全相似度。
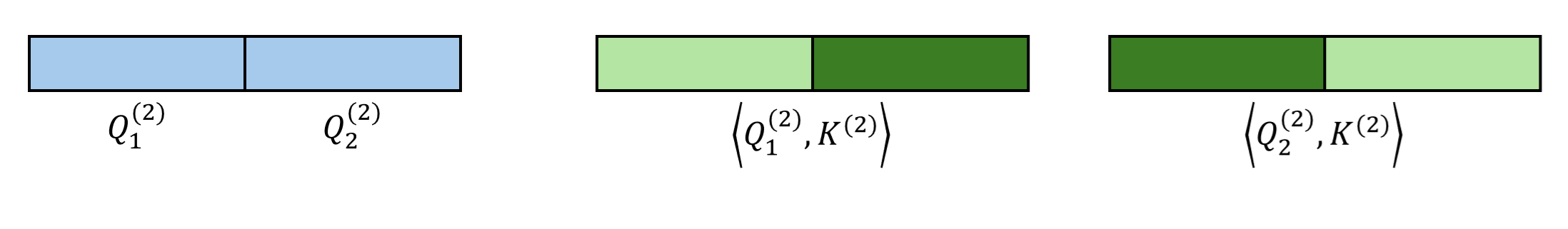
从第二粗糙级开始,我们递归地利用前一级的稀疏索引来再次选择 Top-$K$ token。这里,我们认为一个大 block 内所有精细 query 在这一级里拥有相同的 sparse pattern。比如下图中的 $\mathbf{Q}^{(1)}_1, \mathbf{Q}^{(1)}_2$ 都属于更粗糙的 $\mathbf{Q}^{(2)}_1$,它们应该只关注 $\mathbf{K}^{(2)}_2$ 对应的 key token。
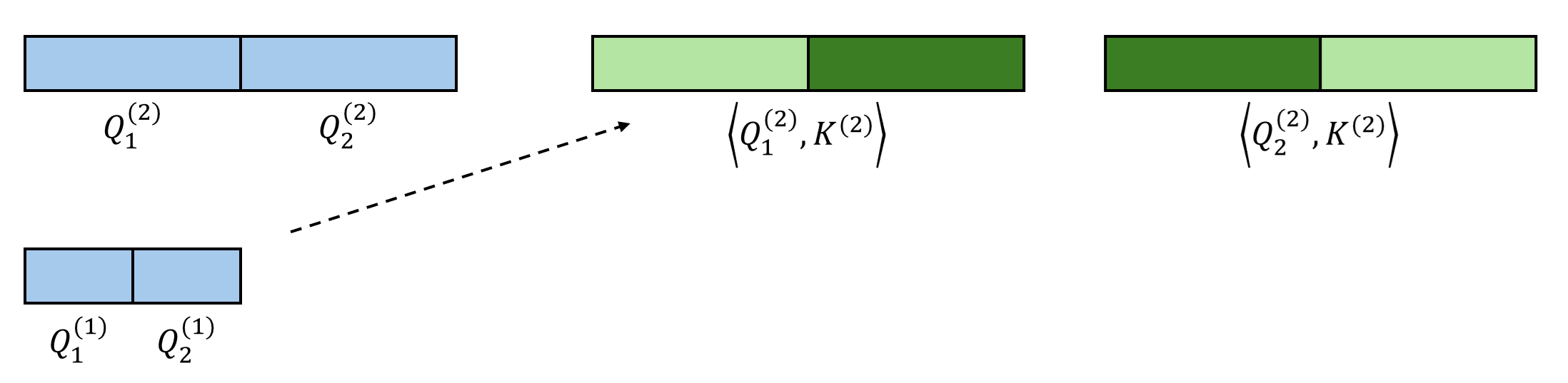
每个 query 在前一级里有 $K$ 个候选粗糙 key block。而到了这一级后,由于特征的精细度增加,每个 query 有 $KB$ 个候选 key block。对每个 query 的 $KB$ 个 key token,我们再执行 Top-$K$ 选择算法。算法递归执行,直到最底层。
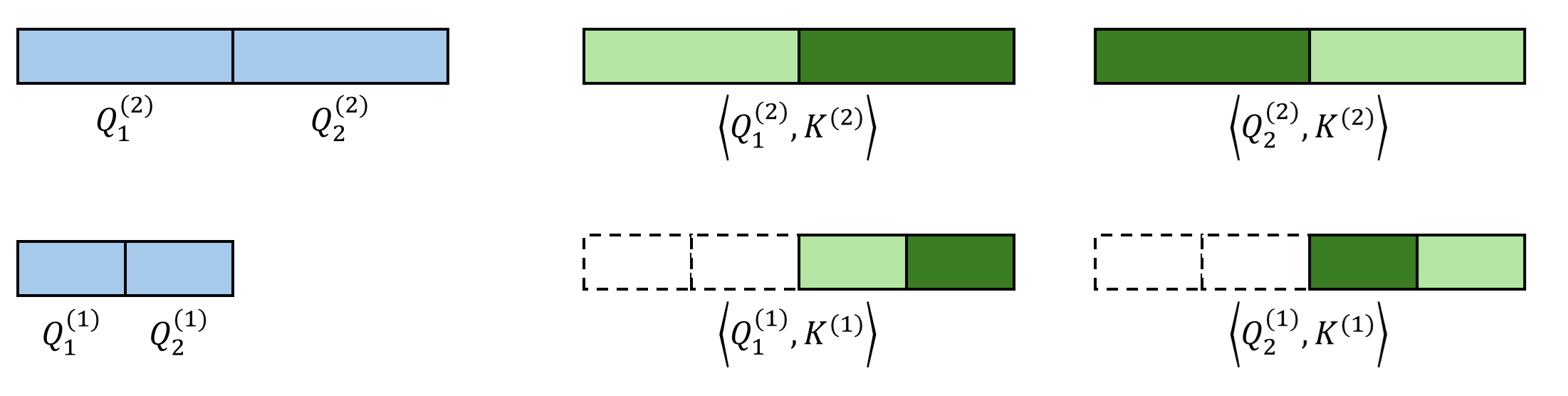
最终,和以往稀疏注意力算法一样,我们能给每个最精细的 query block 找到 Top-$K$ 个最精细的 key block。此外,我们还知道了每个 query block 在每一级 key block 中应该关注哪些稀疏 key block。
层级 KV 丰富化。在标准稀疏注意力中,只关注稀疏 K, V token 不可避免地会带来信息损失。
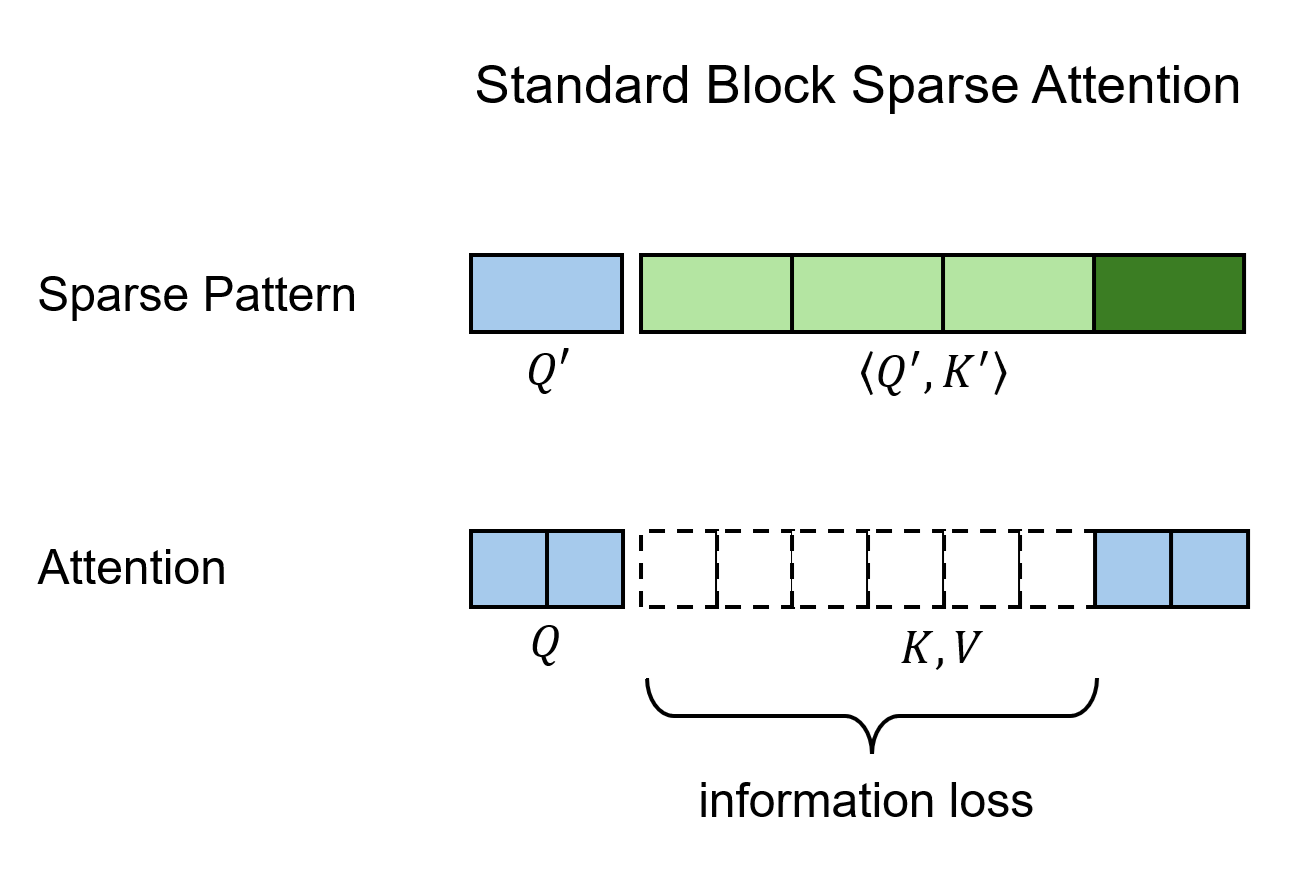
而 LLSA 在层级 Top-$K$ 选择中发现的多层级 sparse pattern 恰好能缓解这一点。相比于只看最精细的 K, V token,LLSA 还会在最后的稀疏注意力计算中把各级的粗糙 K, V token 考虑进去。这样做能让每个 query 不丢失全局信息。
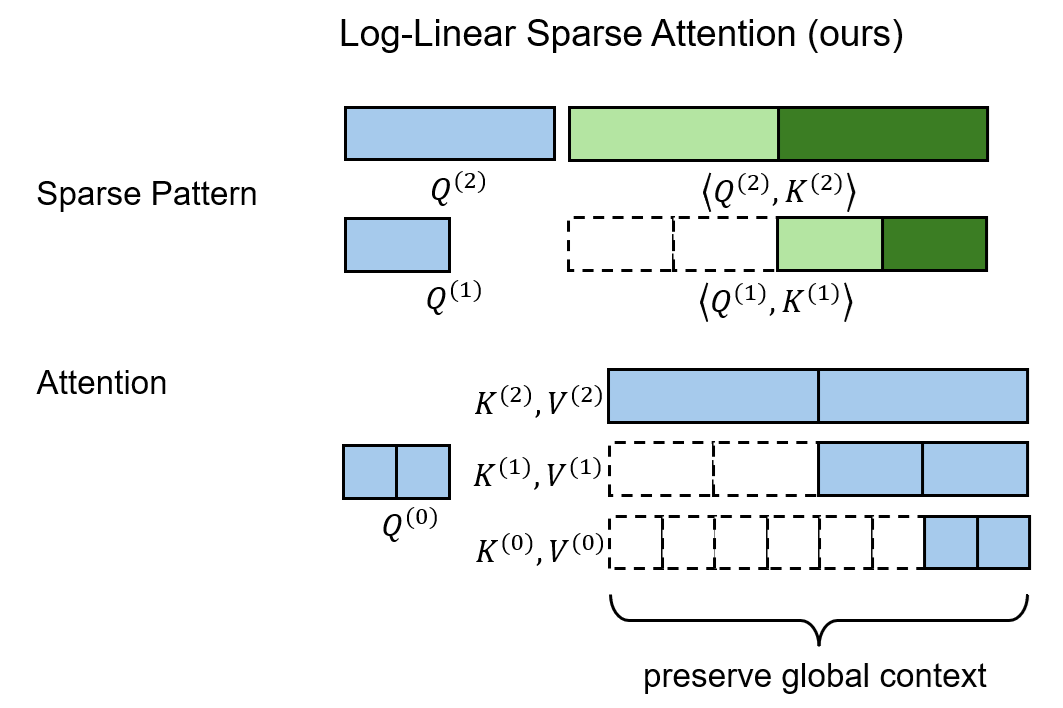
KV 权重重设。上一节讲的做法还不是最优的。按理来说,更粗糙的 token 拥有的信息更多,应该更重要一点。但在默认做法下,我们只会给所有层级的 K, V token 设置相同的权重。
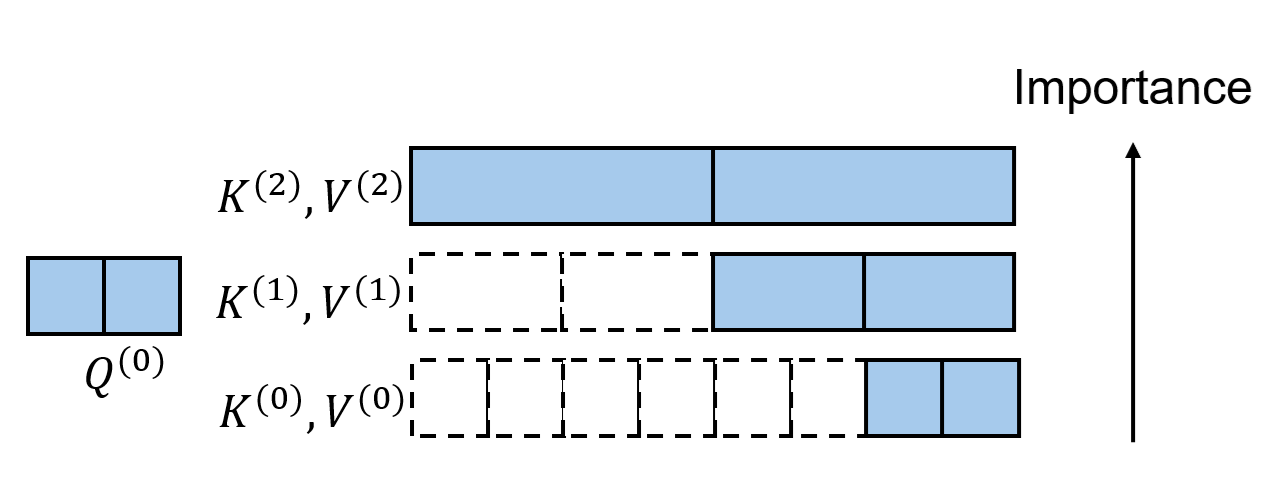
为此,我们假设一个 coarse K, V token 里所有精细 token 的信息可以通过最近邻上采样(或者说 repeat 操作)复原出来。按照这个假设,我们不需要真的去做上采样,而只需要在注意力运算中给不同层级的 token 设不同的权重就行。具体来说,第 $l$ 级 token 的权重为 $B^l$。这个权重会乘到 K 和 V 上。
复杂度分析
说了这么多,LLSA 真的比之前的稀疏注意力更快吗?让我们来分析一下它的复杂度。(假设 $B$ 是常数)
在层级压缩部分,只需要对总 token 数计数。不同层 token 数量构成一个等比数列,该数列的和小于一个与 $B$ 相关的常数乘以 $N$。所以复杂度是 $O(N)$。
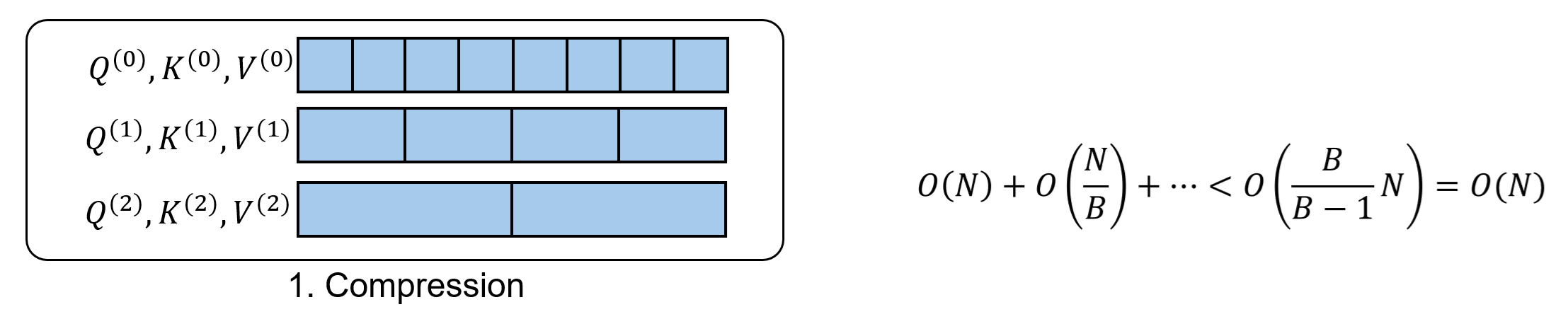
同理,在第二步层级 Top-$K$ 选择中,参与计算的 query 数加起来是 $O(N)$ 个。每一级要算相似度的 key token 数有 $KB$ 个,最终的复杂度是 $O(NK)$。
为了节省篇幅,这里我们没有分析 Top-$K$ 的复杂度。Top-$K$ 的复杂度取决于其算法实现。这一部分的运行时间其实和具体的数据长度、使用的并行算法相关,对 $K$, $B$ 的复杂度分析意义不大。但不管用什么算法,如果 $K$, $B$ 都是常数,仅考虑 $N$ 的增长的话,Top-$K$ 这一步的复杂度也是 $O(N)$。

在最后一步注意力计算中,有 $O(N)$ 个 query,有 $O(K\log N )$ 个 key, value block。这一步的复杂度是 $O(N K \log N )$。
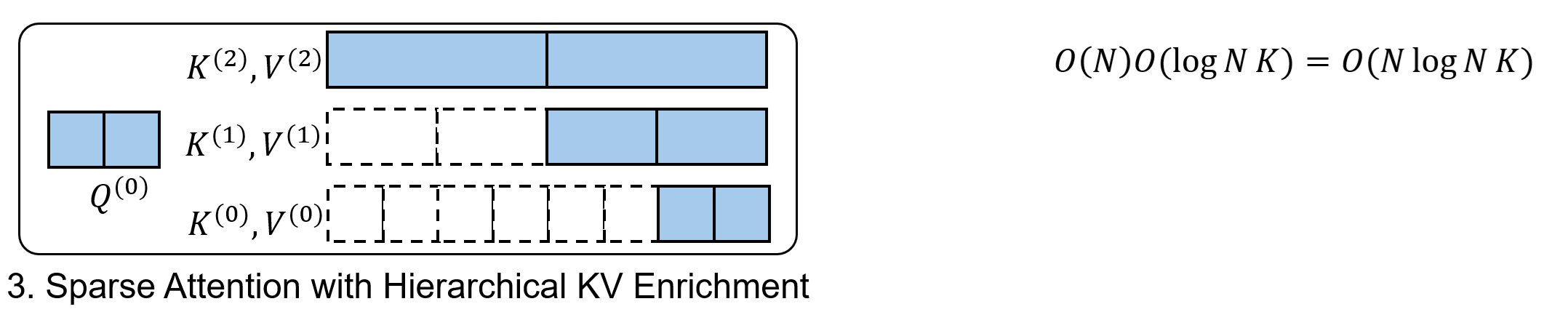
如果我们把 $K$ 也看成常数的话(实践中是这样的),整个 LLSA 的复杂度就是 $O(N\log N)$。我们成功把以前稀疏注意力 $O(N^2)$ 的复杂度降下来了。
高性能 GPU 实现
在现代深度学习框架中,设计新算子时必须要考虑它是否能兼容 GPU 并行运算。而 LLSA 在设计时,始终是兼容 FlashAttention 这种现代 GPU 实现的。
具体来说,在所有涉及稀疏访问的部分 (稀疏 Top-$K$,稀疏注意力),只需要把原来对于所有 K, V 的遍历换成对于稀疏索引的遍历,再根据索引去 gather K, V 的值即可。原来复杂度为 $O(N)$ 的循环都会被优化至 $O(K)$。
但在编程实现时,有一处难点:Top-$K$ 算法只能获取 Q-major 的稀疏索引(即哪些 Q 能看到哪些 K),但不能直接获得 K-major 的稀疏索引 (即哪些 K 能看到哪些 Q)。而在对 K, V 求梯度时,得用到 K-major 的稀疏索引,才能实现高效的求梯度算法。所以,我们要实现一套从 Q-major 索引到 K-major 索引的稀疏索引转置算法。

幸好这方面的研究在稀疏矩阵乘法领域已经很成熟了,我们直接把成熟的算法用了过来。我这里简单介绍一下算法的思想。由于每个 K 对应的 Q 的数量是不等长的,我们只能把所有 Q 索引存到一个一维展平的数组里。它相当于把不等长的二维 K-major 索引 flatten 成了一维。为了知道每个 K 用的是哪些索引,我们再用另一个辅助用的 offset 数组,表示每个 K 的开始、结束 offset。
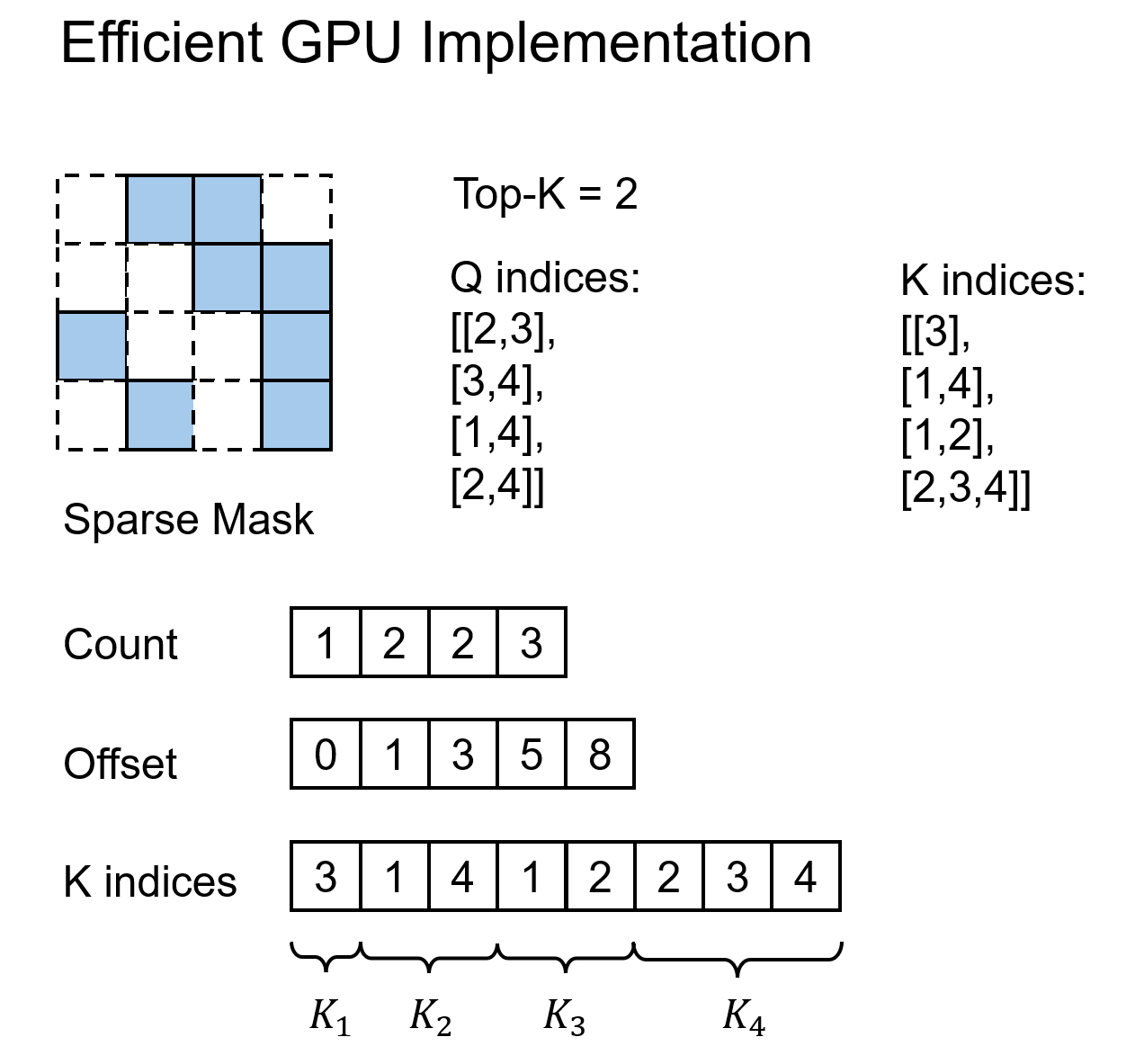
如果不用这个优化过的算法的话,就得用一个稠密的 mask 矩阵来表示每对 Q, K 之间是否有效来间接描述稀疏性。这样算法的复杂度会退化到 $O(N^2)$。此前不少方法都用的是这个更低效的算法实现。
实验
Pixel DiT 实现
为验证 LLSA 确实能降低注意力的复杂度,我们在长像素 token 序列上训练了一个无 VAE,无 Patchification 的像素 DiT。为了将 LLSA 适配到二维数据上,我们使用了索引重排。为了加快训练速度,我们使用了噪声重缩放和低分辨率预训练。
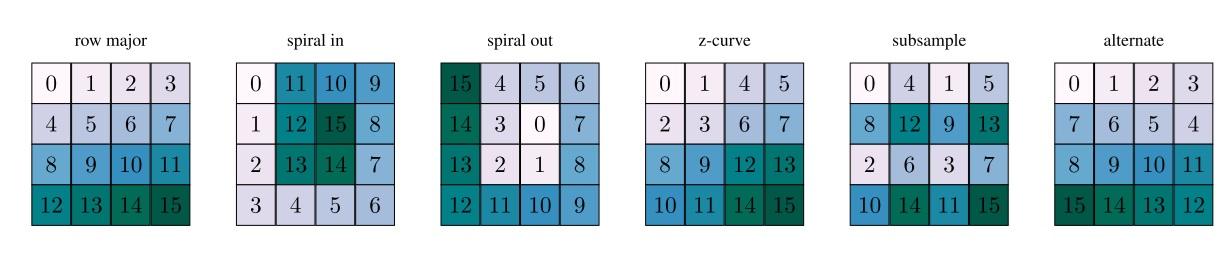
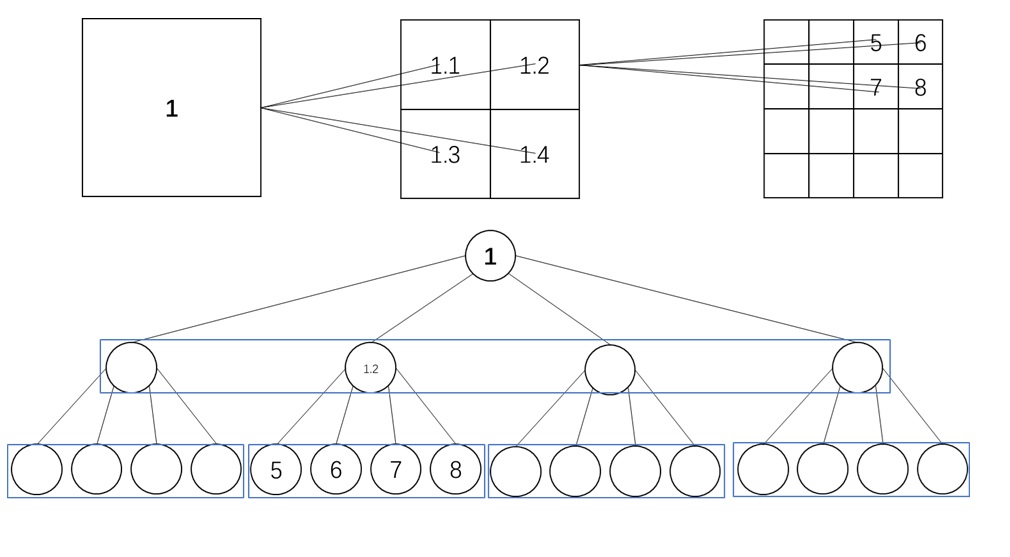
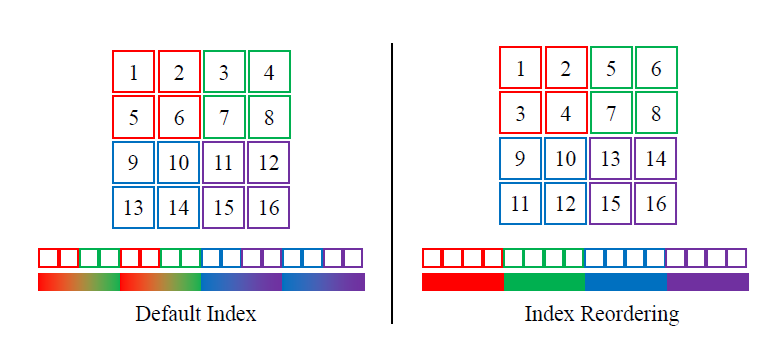
索引重排。LLSA 其实是为 1D 序列设计的。由于其中存在对相邻 $B$ 个 token 做平均下采样的操作,我们最好能保证相邻 token 的性质相似。而对于 2D 图像,最自然的做法是令 2D patch 的 1D 索引尽可能相邻。于是,我们参照之前的工作,设计了下面的索引重排方式。
噪声重缩放。之前 Simple Diffusion, SD3 等工作表明,高分辨率的数据应该加更多的噪声。在我们的实验中,发现最好的提升噪声强度的方法就是在噪声前乘一个系数 $s(s\geq1)$。比如对于 rectified flow 加噪公式:
根据实验结果,对于序列长度为 $n\times n (n>64)$ 的图片,我们令 $s = n/64$,也就是把信噪比对齐至 $64\times 64$ 的图片。
预训练。参考 SD3 等大型文生图模型的多阶段训练方式,我们先在低分辨率图像上预训练模型,再逐渐在高分辨率上微调。
DiT 模型。我们把标准 DiT 的位置编码换成了 RoPE,并且加上了 qk-norm 以稳定 bfloat16 的训练。
我们没有把 backbone 升级成 LightningDiT 或 DDT,也没用 REPA。
指标。除非有额外声明,论文中指标的默认配置为:FID 是用 10,000 个经过 20 步去噪生成的图片来计算的。吞吐量的单位是 1,000 像素 token / 秒。使用的 GPU 是单卡 H200。
消融实验
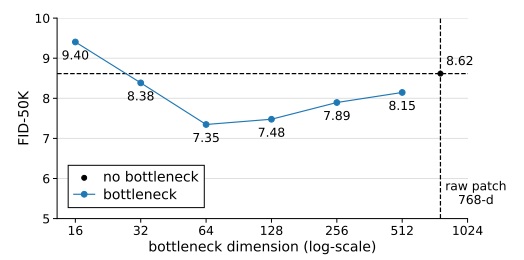
消融实验默认是在 FFHQ-128 上训练了 20 epoch 的模型上测试的。所有实验中,默认情况下,超参数 $B=16$, $K=8$。我们简单看一下主要的消融实验结果。
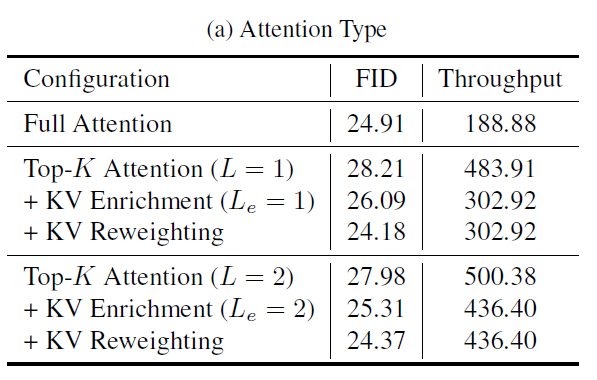
表格中,$L$ 是层级数,$L_e$ 表示多少级用了 KV Enrichment。能得到的结论有:
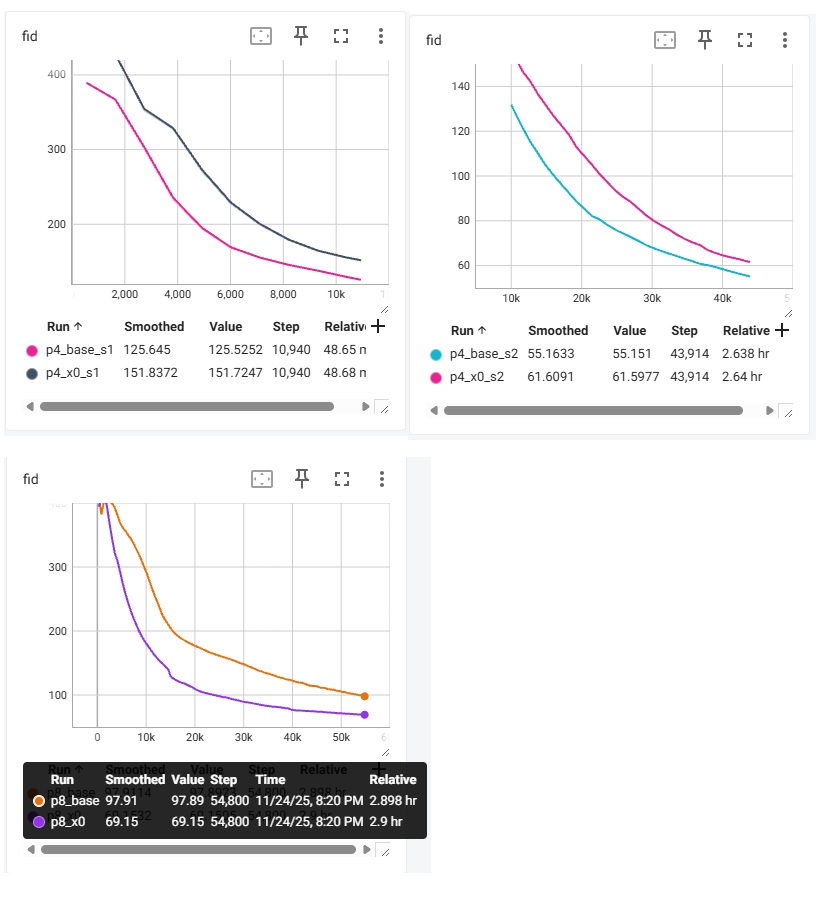
比较 $L=1$ 和 $L=2$ 的结果,能发现换成 $L=2$ 显著提升了速度,同时 FID 略微变差(变差的主要原因是用到的 KV token 数大幅减少)。这证明了 LLSA 划分成 $\log N$ 层级设计确实能够提升计算效率。
KV Enrichment 和 KV Reweighting 都很有效。最后甚至稀疏注意力的 FID 比全注意力还好。
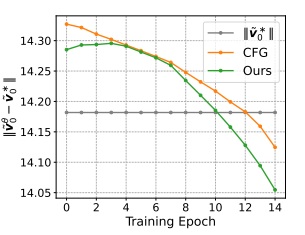
我们还尝试在 $512 \times 512$ 的 FFHQ 上训练 $L=3$ 的 LLSA。结果也完全符合预期:在序列变长时增加 $L$ 能使得模型速度几乎按 $O(N \log N)$ 增长,但因用到的 KV token 变少,效率提高,质量会稍差一点。
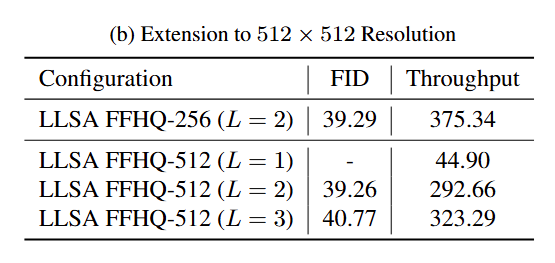
论文正文和附录里还有更多消融实验结果。最终的结论是,注意力和训练方式中的每一项设计都是有效的。
对比实验
在对比实验中,我们比较了 VSA,SLA 这两种方法。这里也顺带介绍一下 VMoBA。据我所知,近期做 DiT 可训练稀疏注意力的工作就是这三个。仅看使用哪些 key block,忽略各个方法对图像/视频的处理细节,各方法的做法为:
- VMoBA:VMoBA 和 MoBA 都等价于上面表格里 Top-$K$ Attention。
- VSA:对平均池化后的 Q, K, V 算一个粗糙注意力输出,把它和稀疏注意力的输出相加。
- SLA:用另一个线性注意力拟合 Top-$K$ 以外的 K, V 输出,把它和稀疏注意力的输出相加。
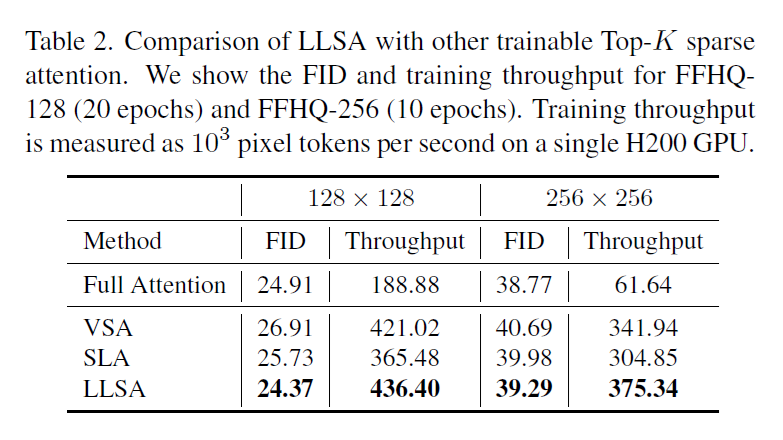
为了保证对比实验的公平,我在同样的训练环境下用尽可能相同的超参数进行了实验。具体来说,我把 VSA, SLA 的代码搬进了我的训练环境下。由于它们的 GPU 反向传播实现较为低效,为了公平地比较算法速度,我把 VSA, SLA 的反向传播也升级成了稀疏索引卷积的版本。此外,由于我们启用了 KV Enrichment,对于同样的 $K$,LLSA 在稀疏注意力计算时会访问更多 K, V token。为了质量对比上的公平,我们增加了 VSA, SLA 的 $K$,使得它等于 LLSA 在稀疏注意力时实际访问的 K, V 数量。
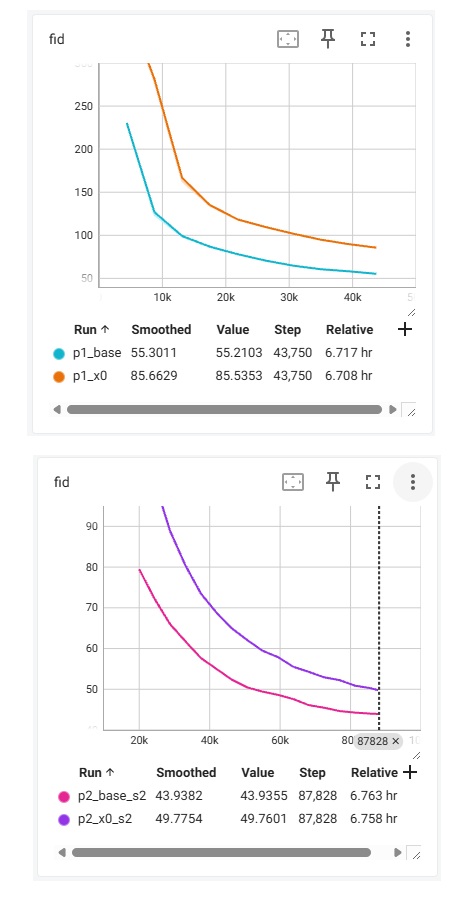
在 FFHQ 上的对比如下。LLSA 又快又好。
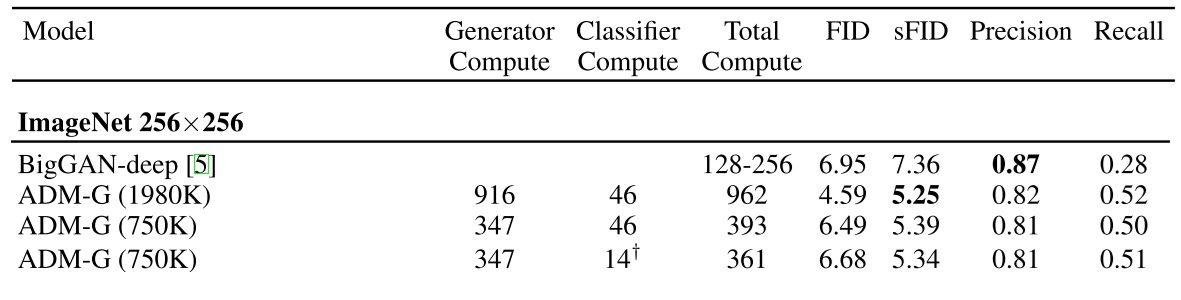
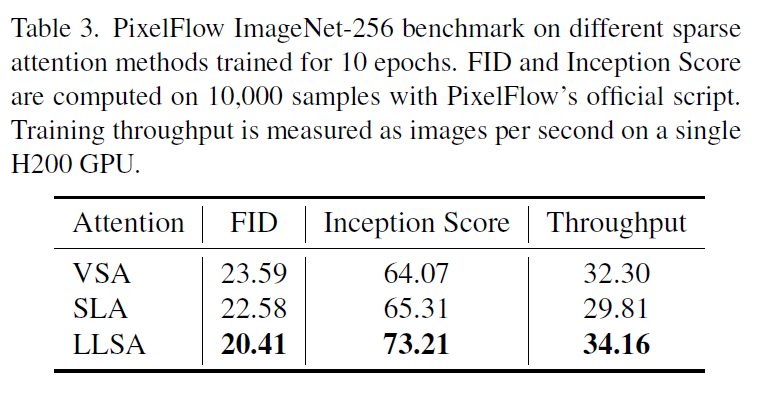
我们也尝试了 ImageNet-256 上的验证实验。为了在有限的时间内完成训练,我们以 patch size = 4 的 PixelFlow 为 DiT backbone,将其中的全注意力替换成 VSA, SLA, 或 LLSA。训练 10 个 epoch 后的结果如下。
前四个 epoch 训练时的指标如下。
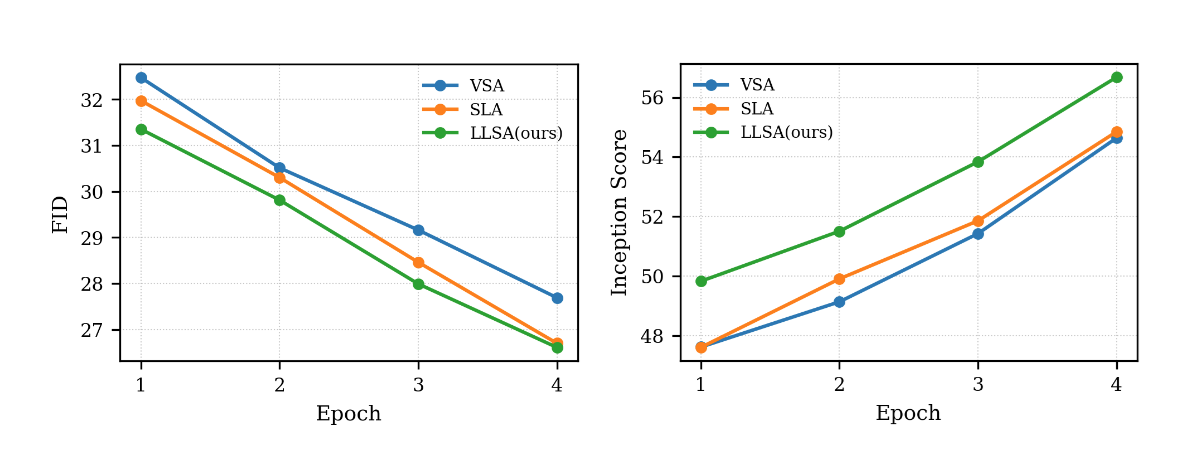
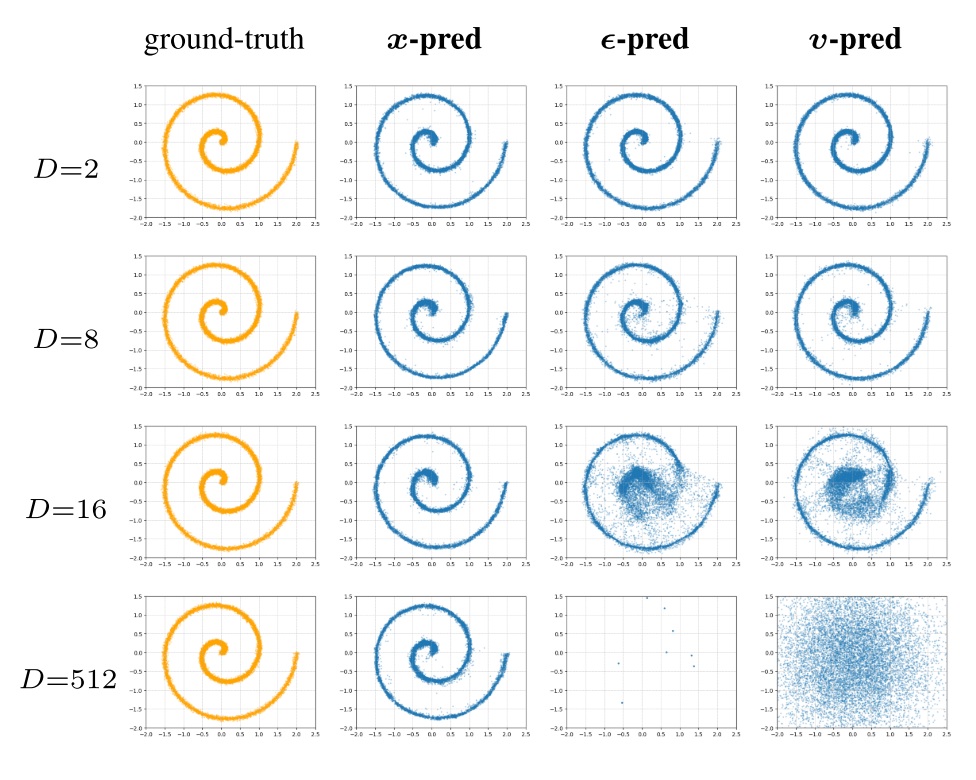
可以看出,哪怕是在实验配置较保守的情况下,无论是在 FFHQ 还是在 ImageNet 上,LLSA 都比之前的稀疏注意力又快又好。这个实验结果其实很正常。在设计注意力时,我尝试了很多处理粗糙 K, V 的方法。最后发现,如果像 VSA, SLA 一样引入多个计算 branch 再把结果相加,效果怎么都比不过只做一次注意力。可见,哪怕忽略 $O(\log N)$ 加速那一块,将池化后的 K, V 和原来的精细 K, V 一起做注意力的做法在生成质量上优于之前的处理方法。
效率
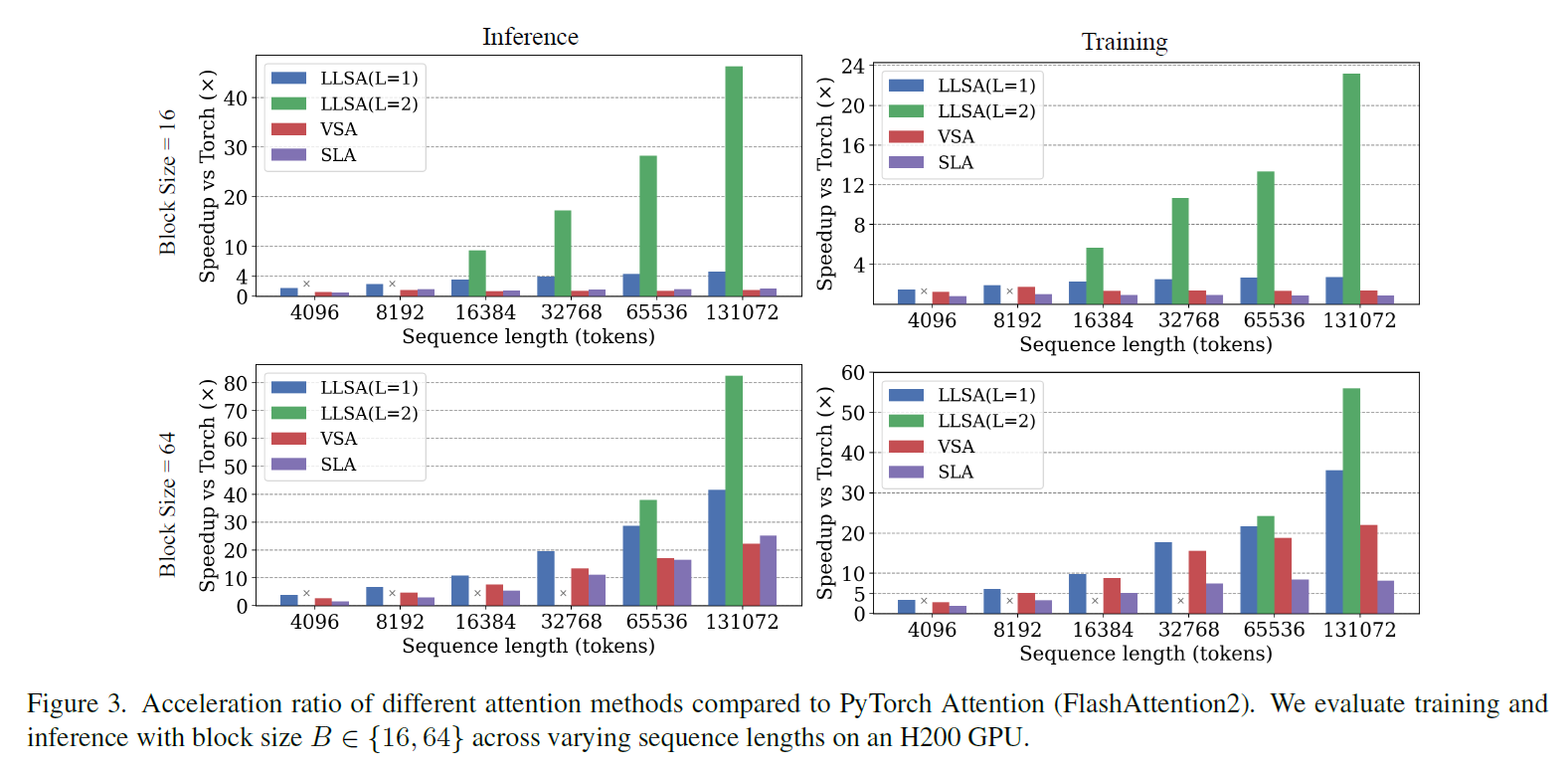
我们单独比较了不同 $B$ 时各个注意力方法在不同序列长度下推理和训练的耗时(用相比全注意力的提速比表示)。当然,这次我们用的是未优化的 VSA, SLA 代码。LLSA 有着肉眼可见的效率优势。
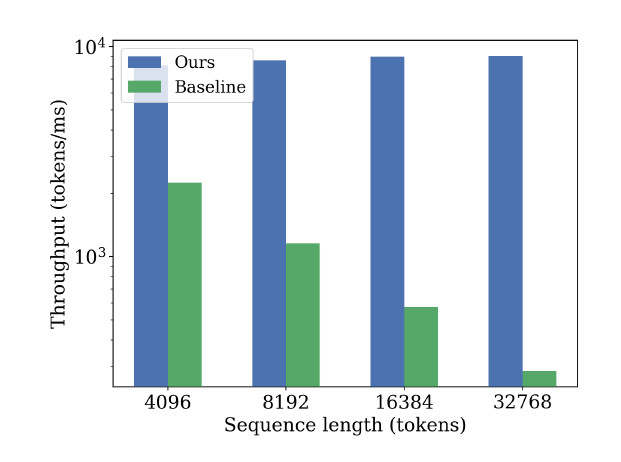
我们还验证了用稀疏索引转置实现反向传播的有效性。我们比较了 LLSA 的反向传播实现和 baseline 反向传播实现的速度,其中 baseline 是通过 dense sparse mask 实现的。由于我们的算法是 $O(N)$ 的,在不同序列长度下吞吐量几乎不变。
这些实验说明,在 GPU 编程实现上,LLSA 也做得比以前的方法更好。
论文评价
赞美的话就不必多说了。从实验部分可知,LLSA 无论是算法设计的效率上、质量上,还是 GPU 编程实现的效率上,都比之前的同类方法好。
这篇论文有两个明显的缺陷。
先挑那个最严重的缺陷。这篇论文没有展示 ImageNet-256 上一个完全收敛的 DiT 的指标,只展示了少量训练轮数时的结果。因此,没有证据表明在扩大模型规模、数据集规模后,LLSA 还能有效。如果能补上这些实验,论文的说服力会大幅提升。
请给我一点反驳的空间。事实上,从项目开始之初,我就对这个潜在缺陷心知肚明。我们不展示这个实验不是不想做,而是我们无法承担如此大的训练代价。我们的 LLSA 只有在 token 数很多很多的时候才能体现出优势。为此,我们要刻意找这样一个 token 数很多的任务。之前的 VSA, SLA 等方法是在预训练视频 DiT 上验证他们的方法,这样的视频任务用的 token 很多,确实很合适。但他们用到的实验数据、测试方法都不太统一。并且,VSA 论文明确指出他们在实验中用到了 128 块卡,我拥有的 GPU 远少于这个数。因此,无论是从验证方法的公平性还是计算资源上,我都不打算选择视频生成任务。高分辨率像素 DiT 生成算是一个最公平,最清晰明了的任务了。然而,即使是这样的任务,由于 token 数很多,我们也没办法像其他带压缩的 ImageNet-256 上的 DiT 一样训那么久。一般来说,这些 DiT 的压缩比都是 $16 \times 16$ 倍,哪怕在最理想的情况下,模型运行时间按线性增长,我们也需要 $256$ 倍的计算资源才能和他们训练同样的轮数。当我们选择了优化注意力复杂度这个目标时,没有资源训练一个收敛得较好的模型就是注定的结局了。我们只能退而求其次,在少量的训练轮数上比较各个方法。
另一个缺陷是论文对于层级设计的有效性没有做分析,缺乏一点「理论分析」上的支撑,更多的是展示工程实现细节。
这个缺陷倒不是很严重,有不少的注意力优化的论文都是只讲实现方法的。缺乏理论、动机上的解释仅仅是降低这篇论文在审稿时的评价,并不会影响方法本身有效性,因为有效性主要还是靠实验来支撑。如果审稿人问到了这一点,也只能俯首道歉。
最后还有一个注意力优化内行才能看出的点。这篇论文的方法设计和 Multi-Resolution Attention 几乎一样,区别仅在于 Multi-Resolution Attention 没提供高性能实现。是否说明这篇论文的创新性不够?
说实话,这个项目刚开始时,我是以优化 NSA, VSA 这些论文为目标,压根不知道早期已经有了一篇 $O(\log N)$ 分级的论文。当然,我也从没觉得这样的优化方案别人想不到,毕竟这样的算法优化策略在计算机科学中十分常见。但是,在我看来,编写一份高性能 GPU 实现是一件有挑战性且贡献足够的事情,提供一份可供社区直接使用的高效实现至少占了论文一半以上的贡献。所以,哪怕之前有方法一样的论文,基于 FlashAttention 重新实现,并在超长序列上验证,已经有足够的贡献了。不仅如此,如前文所述,这篇论文还提供了与层级注意力无关,仅与稀疏注意力实现相关的算法优化贡献,这个优化方法能够直接改进之前 VSA, SLA 的代码实现。综上,我认为算法设计上的雷同不影响论文的贡献度。
未来方向与个人感想
在想出了这套优化复杂度的算法后,我就对这个项目的应用前景充满了信心。哪怕一开始不会 GPU 编程,我也义无反顾地投入了一两个月的时间去学习 Triton 编程并实现了一版高效的算法。在后来的实验中,我也碰到了不少意外之喜。KV Enrichment 和 KV Reweighting 出乎意料地有效。这样,我们方法不仅仅有速度上的改进,在效果上也有不少提升。我非常希望我们的这项研究能够用在更广泛的场景中。
但正如前文所讲,自项目开始之初,一种不祥的预感就萦绕在我的心头:由于长序列生成与高计算量绑定,我们难以训练一个充分收敛的 DiT。同时,我们实验室的主攻方向是 CV 应用,我们也不知道是不是在 NLP 里验证这个方法是不是成本更低一点。最终,我还是选择了尽可能简单的 Pixel DiT 生成任务。我在很长一段时间里都在黑暗中探索验证实验的设计方法,实验结果大多是不令人满意的。我时常会想,假如我是在 DeepSeek 这样的大公司里做这样的研究,会不会更加顺利一点?同样的方法,如果是在更高的平台上打磨,更难的任务上验证,会不会受到的评价更高一点?但学校实验室自然也有实验室自己的做法。在有限的时间和有限的资源内,我敢说我已经充分用科学的实验方法小规模地验证我们方法的有效性了。从现有实验的迹象来看,我对 LLSA 在任务规模扩增之后的表现充满信心。未来犹未可知,那就不必多想。
在维持现有资源的情况下,我的计划是尝试在 ImageNet 上训一个较好的使用 LLSA 的 DiT。最近正好有不少这方面的研究,比如 PixelDiT。我想尝试能否在不显著增加计算量的前提下,在模型的某个地方用 LLSA 算所有像素间的注意力。比如,不改 PixelDiT 带 patchify 的编码器部分,只是提升解码器注意力的计算量。但我近期的实验表明,这样的改进没啥用,还是得让整个 Transformer 都不用 patchify 才行。目前,我仍在做低成本的尝试。
如果非要换一个验证思路的话,我们想到的另一个方案是 4K 图像生成。可以拿一个预训练的 FLUX 在超高分辨率图像数据集上微调。之前有方法做了类似的事,但它们都用的是 window attention。换成 LLSA 按理来说效果会好很多。但这种应用导向的工作所需的工作量较多,且重心也从注意力设计转移到了一个具体任务,适合当成一个全新的研究来做。
当然,我觉得最高效的拓展方案还是寻求合作,争取在 NLP 任务或者视频 DiT 生成任务这两个更加常见、合适的任务上验证 LLSA。如果是做 NLP 任务的话,我需要去结识一些 NLP 领域优化注意力的研究者,寻求他们的意见。而做视频生成任务最大的瓶颈应该是数据和算力,我们需要找公司的视频 DiT 团队合作。鉴于这篇论文已经是在研究注意力方法本身了,如果要继续研究,不应该是小打小闹地微调现有视频模型,最好是在大规模训练阶段一直使用 LLSA。
如果完全忽略相关领域合作者和计算资源这些客观制约因素,我觉得 LLSA 真正大展身手的舞台是此前一些因为注意力平方复杂度而完全不敢做的任务,比如基于体素的 3D 生成。实际上,今年已经有使用稀疏注意力的 3D 生成工作。比如 Direct3D-S2 直接把 NSA 适配到了 3D 生成领域,用于生成至多 45K 个 3D latent。如果未来 GPU 的性能能按线性持续提升,且某任务的质量直接取决于 token 的数量,那么 LLSA 一定有很大的发挥空间,因为它确实能将全注意力的复杂度降下来。
总结
在这篇论文中,我们介绍了 Log-linear Sparse Attention (LLSA),一种将自注意力运算复杂度从 $O(N^2)$ 降至 $O(N \log N)$ 的新颖注意力机制。它的贡献有:
降低稀疏注意力复杂度的层级式设计,可以应用到现在所有类型的稀疏注意力中。
提出了 KV Enrichment 这种相较 VSA, SLA 更优的维持全局信息,利用稀疏 K, V 的稀疏注意力方法。
实现并开源了高性能 GPU 程序。它不仅能够直接被后续工作使用,它的 GPU 编程思路也可以启发后来的工作。
我觉得 LLSA 未来可期。如果让我主导视频 DiT 的训练,我一定会立刻把全注意力换成 LLSA。
我在 MLSys 方面的积累不足,论文和研究方法或许有可以改进的空间。我们欢迎各种形式的合作,包括但不限于:
- 对论文内容的批评与建议。
- 学校实验室的科研合作。
- 公司的实习、项目合作。
我未来会持续宣传、介绍论文的内容。已经定好的事项有论文内容以外的独家解读博文(这篇博文其实只是重述了论文的内容)。有机会的话我也会分享这次科研过程中艰辛的历程。视频介绍可以做,但感觉这种类型的论文不太适合做成视频。大家有什么疑问,建议,也欢迎多多交流。
参考文献
Attention:
(FlashAttention) FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
(MoBA) MoBA: Mixture of Block Attention for Long-Context LLMs
(NSA) Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention
(SpargeAttention) SpargeAttention: Accurate and Training-free Sparse Attention Accelerating Any Model Inference
(Sparse VideoGen) Sparse VideoGen: Accelerating Video Diffusion Transformers with Spatial-Temporal Sparsity
(VMoBA) VMoBA: Mixture-of-Block Attention for Video Diffusion Models
(VSA) VSA: Faster Video Diffusion with Trainable Sparse Attention
(SLA) SLA: Beyond Sparsity in Diffusion Transformers via Fine-Tunable Sparse-Linear Attention
(MRA) Multi Resolution Analysis (MRA) for Approximate Self-Attention
(Radial Attention) Radial Attention: $O(n\log n)$ Sparse Attention with Energy Decay for Long Video Generation
Log-Linear Attention
Pixel DiT:
(PixelFlow) PixelFlow: Pixel-Space Generative Models with Flow
(PixNerd) PixNerd: Pixel Neural Field Diffusion
(JiT) Back to Basics: Let Denoising Generative Models Denoise
(DiP) DiP: Taming Diffusion Models in Pixel Space
(DeCo) DeCo: Frequency-Decoupled Pixel Diffusion for End-to-End Image Generation
(PixelDiT) PixelDiT: Pixel Diffusion Transformers for Image Generation