计算是什么呢?
数学,一门从数字与计算中出现的学科,在发展到一定阶段后,开始追问起了计算的本质。
数学家们用数学的语言,把“计算”这个早就存在的词语严格定义。用自身定义自身,这正是数学之美。
更令人开心的是,数学家在研究计算的过程中,开创了计算理论这门学科。人们在计算理论的基础上,制造了计算机。再随着计算机的应用不断变广,计算机成了一门单独的学科——计算机科学。
又扯远了。计算理论研究了什么是计算的机器,哪些问题是人们可以计算出来的,可以计算的问题怎么才能计算得更快。为了开始计算理论的学习,我们需要从最简单的计算模型,来一步一步理解计算理论研究的内容。有穷自动机及正则语言,就是我们的第一个学习对象。
第1章 正则语言
事物的状态
每时每刻,世界的万物都在发生变化。比如,昼夜不断交替着,早晨太阳升起,傍晚太阳落下;今天的我,总是比昨天的我更加帅气一点。
有些变化,它变来变去就是那么几种情况。比如,天要么是亮的,要么是暗的。有些变化则不然,是会一直进行下去的。我每天都在变帅,我的帅气程度永远在递增,不会有两个相同的值。
为了更好地掌控那些状态有限的事物,人们用一个有向图来表示这些事物。在有向图中,顶点表示状态,边表示转移条件。比如
黑夜——————-太阳升起————————> 白天
<—————太阳落下———————————-
状态,就是事物本质的情况;状态发生转移,就是外界条件对事物的本质产生了改变。
有限自动机
人们在研究一个数学问题是否可以解决时,想到数学问题涉及的内容都可以转化成字符串。问题解决,就是问题对应的字符串在一系列验证过程后,该字符串被认为是正确的。比如问一个十进制数字是否是偶数,所有问题的输入都转换成一个十进制数字字符串。”1”被认为不是符合要求的字符串,”666”被认为是一个符合要求的字符串。而问题的所有解,则是一个字符串集合,也就是一个语言。
于是人们把数学问题转换成字符串是否“正确”的问题。字符串的每一个字符,都会对字符串是否正确产生影响,都会改变字符串的整体性质。联系开始我。们对于状态有向图的分析,状态转移正是事物本质发生变化的过程。我们似乎可以用开始的状态有向图,来判定一个字符串。因此,人们把字符串的每个字符做为状态转移的条件,把一些状态设为“正确状态”,意味着能通过字符一步一步走到这里的字符串是正确的。当然,还有一个初始状态,表示在什么字符也没有读取时的状态。
这样讲还是抽象了一点,还是举个例子吧。假设我们用的字符全部是0(也就是说字母表是$\{0\}$),我们现在碰到的问题是:给定一串字符串,问其长度是否为偶数。我们该怎么样用一个状态有向图来解决这个问题?或者说,如何把所有解表达出来呢?
从本质上来看这个问题,一串只有0的字符串只有长度为奇数和长度为偶数这两种可能。每多加一个0,就会改变字符串长度的奇偶性。也就是说,我们有两个状态:“偶数长度状态”、“奇数长度状态”。在碰到0的时候,两个状态间会互相转移。最开始时,字符串处于“偶数长度状态”,因为我们读入的字符串长度为0,是个偶数。如果我们读完了字符串后,发现我们停留在了“偶数长度状态”,那么这就说明该字符串的长度是偶数。状态图画出来是这样的:
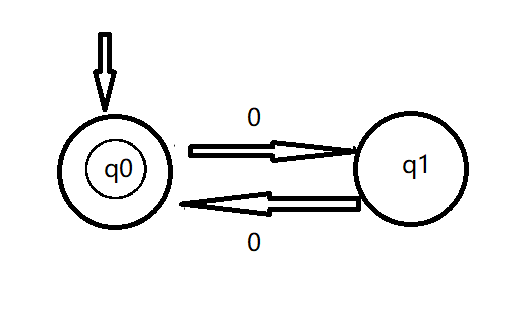
左上角的箭头表示最开始进入的是q0状态,也就是“偶数长度状态”。右边箭头上的0表示转移碰到0就往箭头的方向转移。左边q0状态里面有一个小圆圈,表示这个状态是最终我们能够认可的状态。
我们构建的这个状态有向图,有一个十分大气的名字“有穷自动机”。这个名字为什么这么叫呢?大概有穷,指的是状态数是有限个。自动机,指的是我们只要把字符串到这个有向图里,按照规则在里面走迷宫,我们最终就可以知道这个字符串是否符合我们的要求。整个有向图就像一个自动工作的机器一样。虽然这个名字看上去很厉害,但正如我们分析的一样,有穷自动机就是一个有向图,它的概念十分容易理解。
每一个有穷自动机都可以由5部分确定:$(Q,\Sigma,\delta,q_0,F)$。$Q$是状态(点)集合,$\sigma$是字母表,$\delta$是转移函数(边)集合,每个转移函数接受的参数是当前状态与碰到的结果,输出的是下一状态,也就是说转移函数集合是$Q\times\Sigma\to Q$。$q_0$是初始状态,也就是我们走迷宫的起点。$F$是接受状态集合,$F\subseteq Q$,也就是迷宫的所有终点。我们需要字母表,是因为无论碰到什么字母,我们都得确切地知道我们下一步该往哪里走。我们在转移函数中,必须写清楚每个字母的转移情况。因此也可以得出,转移函数的集合有$|Q|$行$|\Sigma|$列,代表每个点在碰到每个字母转移到的下一个点。
显然这个定义是数学家给出来的。如果是程序员发明这个东西的话,一定会给每个量取一个好听的变量名,以更好地记忆和理解每个量的意思。不过和其他所有的数学定义一样,这些东西是不用背的,只要理解了它们的意思就好了。这些希腊字母和带下标的字母看起来确实让人头疼。
正则语言与正则运算
有一个很重要的名词,我们明明见过它,却只有现在才能介绍它。正则语言,就是某个有穷自动机可以识别的语言。既然有这个定义,就暗示世界上还有很多语言,很多字符串的集合,是有穷自动机表示不了的。话说回来,作为本章的标题,正则语言竟然是通过有穷自动机定义的,真是没有牌面。
但是,正则语言之所以不叫有穷自动机语言,是因为还有一些概念是“姓”正则的。我们之前讲过,所有数学问题都可以被转换成字符串,问题间的运算就转化成了字符串集合运算,也就是语言运算。比如找到两个问题任一的解,就是这个字符串满足问题一的解或者问题二的解。也就是说,问题转化成了语言求并的过程。类似的,语言还可以互相连接(符号$\circ$)、自我重复(符号$\ast$,所以也被叫做星号)。$A\circ B = \{xy|x\in A \bigwedge y\in B \}$,$A\ast= \{x_1x_2..x_k |k \geq 0 \bigwedge x_i\in A\}$。当然,求并和连接是二元运算,自我重复是一元运算。这三种运算都叫做正则运算。为什么这些也“姓”正则呢?因为正则语言在做了正则运算后,还是正则语言,也就是正则语言在正则运算下封闭。
正则语言在正则运算下封闭这个定理是可以证明的。要证明此定理,要分别证明正则语言在3种运算下封闭。不过在当前条件下,我们比较方便证明的只有求并运算。
定理:正则语言在并运算下封闭。
证明:
设原来的语言为$A_1$,$A_2$,状态集合$Q_1,Q_2$。现在我们构造一个新的自动机的状态集合$Q$,它有$|Q_1|\times|Q_2|$个元素,不妨把它们排成$|Q1|$行$|Q2|$列。其中,第$i$行第$j$列个状态表示处于原来自动机$A_1$的第$i$个状态和$A_2$的第$j$个状态。也就是说,我们在新的自动机上完全模拟出了之前两个自动机的状态。
新自动机字母表是之前字母表的并。在新自动机上,每一列状态都按$A_2$的规则向左右转移,每一行状态都按$A_1$的规则上下转移,如果是碰到某个自动机之前不存在的字母,就转移到一个失败状态——不管碰到任何字符都回到自己,且不是接受状态的状态。初始状态是既处于$A_1$初始状态也处于$A_2$初始状态对应的状态。$A_1$接受状态对应行上、$A_2$接受状态对应列上的所有状态都是新自动机的接受状态。
新自动机表示的语言就是前面两个语言的并。因此正则语言在并运算下封闭。
为了证明另外两种运算,我们还需要一个新的工具。
非确定有限自动机
在一个偌大的迷宫中,路径错综复杂,你会怎么办呢?在毫无办法的情况下,我们只能选择像无头苍蝇一样随便选择下一步了。毕竟,不停地往前走总比站在原地强。
有一类比较任性的有穷自动机,它们在碰到了一个字符后,可能选择往多个地方走,甚至拒绝接受这个字符。它们在某个状态的时候,还没碰到下一个状态,就有可能急不可耐地往其它一些状态触发。这样的有限自动机叫做非确定有限自动机(Nondeterministic Finite Automation,NFA),之前我们熟悉的有限自动机叫做确定有限自动机(Deterministic Finite Automation, DFA)。为了节约宝贵的时间,后文用简称来称呼它们。
NFA可以看成是一个会影分身的人在自动机上走迷宫。读取到下一个字符后,他可能会召唤多个自己的分身,和自己走不一样的路;可能拒绝接受这个字符,让自己就此消失。没有读取到字符,或者说读取到空字符$\epsilon$时,它也有可能召唤一个分身。只要有一个分身到达了终点,那么他就胜利了,这个字符串就算是接收。如果怎么也走不到终点,或者他的所有分身都消失,那么字符串就算是拒绝。NFA中的非确定性,就是指在碰到某个字符后,下一步的状态是非确定,可能有多个的。
要严谨地定义NFA的话,只需要稍微修改一下开始DFA的定义。DFA的状态转移集合$\delta$的类型是$Q\times\Sigma_{\epsilon}\to P(Q)$。$\Sigma_{\epsilon}$是原字母表中附加一个空字符$\epsilon$,$P(Q)$是$Q$的幂集,也就是$Q$的所有子集的集合。换言之,在每个状态,碰到了某个字符或不碰到字符后,下一步得到的状态是一个集合,而不是单个状态。
配上图的话,理解NFA会更方便。但由于图不好放,这里就不贴了。随便翻开一本计算理论的课本,或者去网上搜索非确定有限自动机,都能找到一些很直观、易于理解的NFA运算过程图。
NFA是如此强大,它用了一种很赖皮的方式来走迷宫:我尝试当前字符串表示的所有路径,有一条能走出去,就算我能走出迷宫。而在原来的DFA上,我们只能按照规则,一边读字符,一边往前走一步。但令人惊奇的是,NFA和DFA是等价的,每一个NFA都可以找到一个和它对应的DFA。我们还是使用构造性发发来证明这个定理,也就是证明每个NFA都可以转换成DFA。DFA可以转换成NFA是显然的,因为根据定义,DFA就是NFA。
我们再次回顾一下NFA的定义。NFA转移函数的结果,从单个状态,变成了状态的集合。转移函数的结果集合,不是状态集合$Q$,而是幂集$P(Q)$。仔细一想,$P(Q)$的大小也只是$2^{|Q|}$个啊!它的大小是有限的。我们可以构造一个新的DFA,它有$2^{|Q|}$个状态,每个状态对应$P(Q)$的一个元素。要得到这个对应的话,只需考虑到计算机科学常用的二进制就行了。用一个$|Q|$位二进制数来表示子集,某一位是1就代表NFA中这一个状态里有一个分身。NFA是$Q$子集与子集之间的转移,但如果我们把子集看成单个元素的话,那么子集转移就等价于状态转移了。
上面这段话其实不是用来读的,是用来启发思考的。对于一个证明,往往要通过自己的思考来理解,看别人的证明思路一般是很难看懂的。相信看到了二进制,二进制每一位对应原NFA中的一个状态,你就能灵光一闪地想出整个证明过程来了。
现在,我们知道NFA和DFA等价,它们只是名字不同的同一事物罢了。DFA的有关性质,NFA都有。比如,能被NFA识别的语言都是正则语言。
嗯?这说明我们以后可能通过NFA来证明语言的正则性了。正好,我们还差两个正则运算的定理没有证明呢!这两个定理可以用一些直观但不严谨的方法证明。
还是把自动机想象成走迷宫,我们将构造出一台NFA,能在新NFA中走到终点的字符串,就是运算过后的字符串。
先证明连接运算的封闭性,即证明有这样一个DFA或NFA,它可以识别连接后的字符串。但我们手里有的,只有识别之前两种语言的DFA或NFA。如果想用DFA来判定连接后的字符串的话,我们首先要面对一个问题:这个字符串应该在哪个位置拆成两半,使得前一半属于第一种语言,后一半属于第二种语言呢?但NFA就没有这个烦恼。先构造两个语言的DFA,取名为A,B。在机器A的所有接受状态中,连一条$\epsilon$的边到B的初始状态,表示任何一个到了A终点的人都可以影分身抵达B的起点。A的初始状态为新机器的初始状态,B的所有接受状态为新机器的接受状态。NFA没有在哪个位置拆开字符串的烦恼——反正我试遍所有可能就行了。
再证明星号运算的封闭性。根据上面的思路,我们可以构造一台NFA,它的所有接受状态,都连一条$\epsilon$的边到初始状态,表示我们在任何时候从可以尝试把这个字符串“拆开”。但是,星号运算中空字符串一定会被接受,因此我们要额外建立一个初始状态,它一个被接收的状态,有且仅有一条$\epsilon$的边指向原DFA的初始状态。
总算,我们证明了正则运算在正则语言下封闭,它们是一家人,有一样的姓也是理所当然的了。
正则表达式
有了正则运算这一新武器,我们有了一个新的表示语言的工具——正则表达式。如果用一个DFA来表示语言,每次都要画一张图,实在是太麻烦了。但是,使用正则表达式的话,我们只需要用一行文字就可以表达语言了。正则表达式和我们的数字表达式一样,运算符号就是并、连接、星号,“数字”就是空字符、空集和单个字符。数学表达式里有1+1=2,正则表达式里有0*0 = {至少有一个0且全部都是0的字符串}。
等等!DFA可以表示语言,正则表达式也可以表示语言,还没有人说它们是等价的呢!但正则表达式也姓正则,暗示它表达的语言就是正则语言,正则表达式等价于DFA。我们接下来又要用构造来证明这一定理。
唉,要是世界上有这样一台机器就好了。机器只有两个状态,第一个状态是初始状态,第二个状态是接收状态。第一个状态到第二个状态的转移条件是一个正则表达式。我要验证一个正则表达式的字符串,就等价于把字符串放入这个机器中判定。可惜我们的DFA只允许在转移条件上写字符啊!
数学家们向来比较开放,喜欢扩大定义。没有这样的机器,我们就来创造这样的机器。广义非确定有限自动机(GNFA)是一个可以把正则表达式当成转移条件的自动机。为了证明正则表达式和DFA的等价,我们只需要一步一步地把DFA的转移条件变成正则表达式,最后变成我们开始说过的那个梦想中的机器——只有两个状态和一行正则表达式的机器。如果能构造出这样的转换方法,就能证明定理了。
我们这次构造的GNFA,是在原来的DFA上一步一步改造过来的。改造的第一步,是新建两个状态——新起始状态$q_s$,新结束状态$q_e$。在保证正确性的前提下,$q_s$对其它每个点连边,每个点向$q_e$。由于正则表达式包括空集,所以连边总是可行的。我们新建的这两个状态就是保留到最后的状态。我们要删掉其它所有点,并修改转移条件,使得整个GNFA依然正确。
对于任意要删的点$q_{rip}$,对于任意其它点$q_i$,$q_j$,设$q_i\to^{R1} q_{rip},q_{rip}\to^{R2} q_{rip},q_{rip}\to^{R3} q_{j}, q_i\to^{R4} q_{j}$,则$q_i$到$q_j$的正则表达式修改为$(R1)(R2)\ast(R3)\bigcup(R4)$。千言万语,胜不过下面这张图: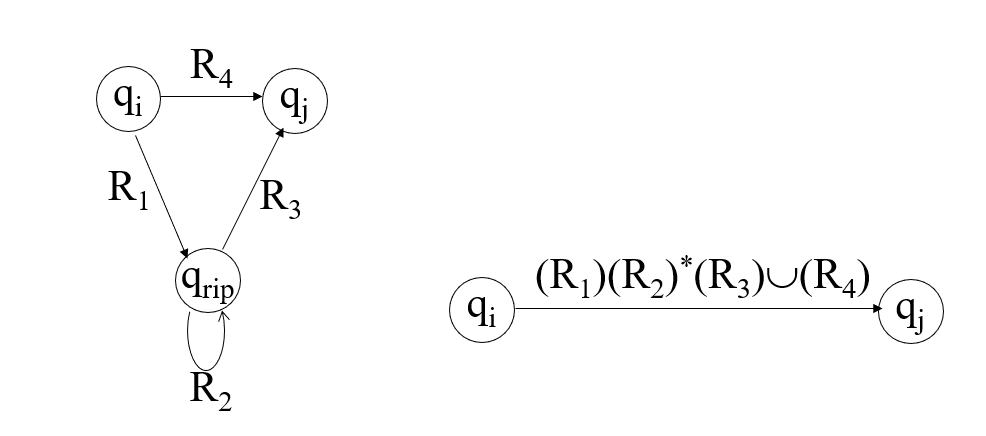
按照这种方法,我们总能在保证正则表达式的意思不变的情况下把中间点删掉。总有一天,我们会删到只剩$q_s,q_e$两个点,这两个点靠一条正则表达式来转移。
我们说明了DFA可以转换成正则表达式。为了证明等价,我们还得证明正则表达式可以转换成DFA。不过这一步要比开始简单得多。
借助证明NFA与DFA等价的方法,我们用如下方法构造NFA,使之与正则表达式等价。一个字符或者是空字符,就连一条边。空集就不连边。并集就是一个点可以通过空字符$\epsilon$移动到并集所表示的两个部分。星号就是结束部分连$\epsilon$连回初始状态,同时再初始状态前加入一个接收状态。同样,说了这么多,不如放一张图:(声明:该图片来自《计算理论导引》(Michael Sipser)第三版 42页)
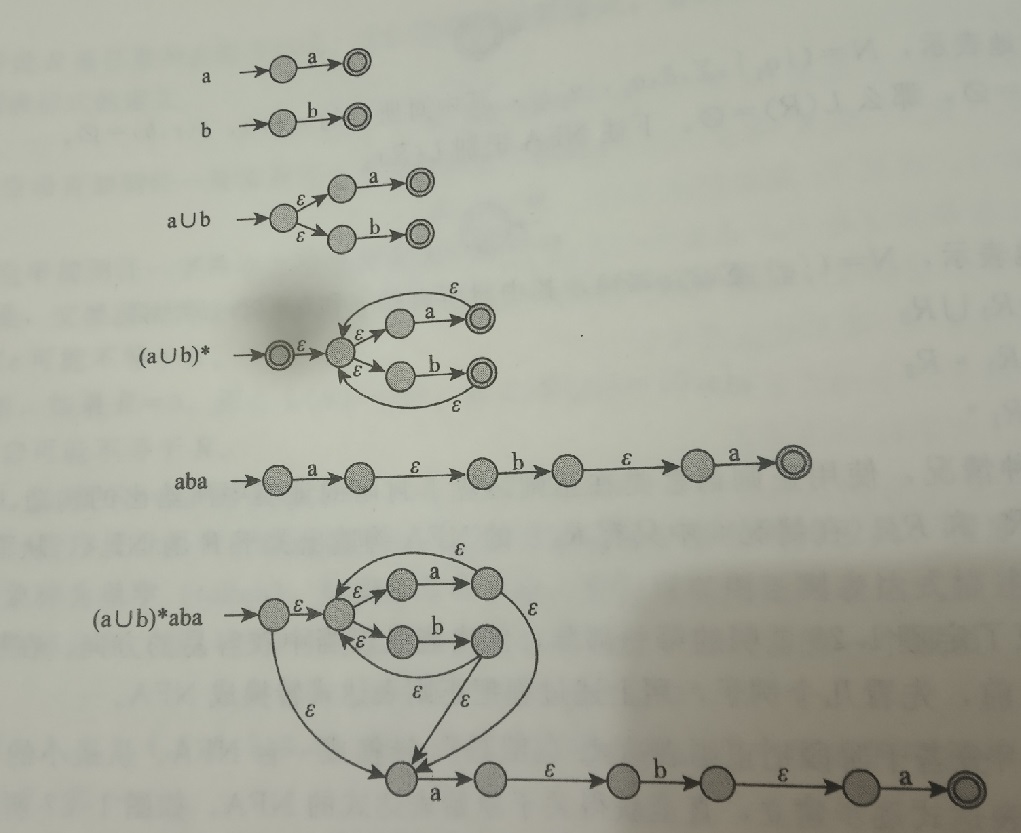
DFA和正则表达式互相转化,那它们肯定是等价的了。
非正则语言与泵引理
开始我们提过,正则语言是可以被DFA表达的语言。换言之,还有许许多多的语言无法用DFA表达。举一个经典的例子:设语言$B = \{0^n1^n|n\geq0\}$,也是说该语言表示0和1个数相同,且先出现0再出现1的字符串。仔细一想,你哪怕使出浑身解数,也构造不出识别这种语言的DFA——为了构造一个这样的DFA,我们必须用状态来存储0的数量,但0的数量可以是无穷大,而状态数的有限的。
但有些愣头青喜欢钻牛角尖,他们偏要说道:“我就不管!你构造不出一台DFA,万一别人构造出来了呢?你凭什么说世界上不存在一台DFA识别这种语言?!”
科学家们又想出了一种证明语言不是正则语言的方法,来应对这些“对知识刨根问底”的热心青年。这种方法用了一个引理,叫做泵引理。
如果一种语言$A$是正则语言,那么$\exists (int)p,\forall(string)s\bigwedge|s|\geq p\bigwedge s\in A \Rightarrow \exists xyz = s \bigwedge xy^iz \in A (i \geq 0)\bigwedge |y| > 0\bigwedge |xy| \leq p$。这一行一阶逻辑,能够让人充分复习离散数学的知识。但是,你很可能看完了也看不懂这一行话要干什么,或者干脆跳过了这行话。
泵引理是说,如果A是正则语言,我们可以随便选一个泵长度p。对于A中的每一个很长很长,长度至少是p的字符串,我们都可以把它拆成3份xyz。其中y部分一定非空,且xy加起来很短很短,长度必须小于p。如果我们在中间不断插入y部分,也就是对于任意字符串$xy^iz,i\geq0$,这个字符串还是A的语言。这个引理中有很多存在和任意,需要仔细地多看几遍。
泵引理的正确性的证明十分诡异。我们需要证明,一个正则语言对应的DFA,它满足泵引理的条件。引理说我们可以随便选一个泵长度p,那么不妨令p为$|Q|$,也就是这个DFA的状态数。对于语言中任意一个长度大于等于p的字符串s,它经过的状态大于等于p+1,因为p+1个状态需要通过p次状态转移,也就是需要读取p个字符。s经过了p+1个状态,但我们总共就只有$p = |Q|$个状态啊!这是怎么回事呢?这说明我们至少经过某个状态两次。我在走迷宫的时候,两次走到了同一个地方说明什么?说明我绕路了!我绕了一圈,又返回了原地。既然我经过了某个状态两次,就必然存在一个状态序列,通过这个状态序列可以回到同一个状态。状态的转移需要读取字符,也就是说,读取了一些字符后,我们又回到了之前的某个状态,我们绕路了。这些字符,我把它重复若干遍,我还是会回到这个状态,我永远会在这个状态绕不出去了。这个字符序列,就是我们拆成三部分xyz中的y。在第一次碰到重复字符时,也就是第一次绕路结束时,我们至多有一个状态走了两次,其它每个状态走了一次,也就是说最多走了p+1个状态,也就是最多读取p个字符,这一部分就是xy,$|xy| \leq p$。至此,泵引理得到一个描述性的证明。
可以发现,泵引理中“存在一个p”这句话一点用也没有,因为我们在证明泵引理时,直接把p钦定为状态数|Q|了。
等等,泵引理有什么用啊?泵引理说明如果A是正则语言,则可以干嘛干嘛。我都知道正则语言可以通过构造一个DFA来判断了,我要泵引理干嘛?
泵引理给出的正则语言的必要条件。也就是说,泵引理的逆否命题,得到的是判断一个语言不是正则语言的充分条件。如果一个语言满足泵引理的逆否命题,那么很遗憾,这个语言一定不是正则语言。
或者再从另一个角度上来讲,我们可以通过反证法来证明一个语言不是正则语言。我们把这个语言套进泵引理中,发现它无论如何都会导出矛盾,那么就可以得出这个语言不是正则语言了。
泵引理反过来是这样说的:对于一个语言A,如果对于任意泵长度p,A中存在一个很长很长,长度至少是p的字符串,我们无论如何都不能把它拆成3份xyz,满足下列所有条件:y部分一定非空,且xy加起来很短很短,长度必须小于p。如果我们在中间不断插入y部分,也就是对于任意字符串$xy^iz,i\geq0$,这个字符串还是A的语言,那么A不是正则语言。我们把整个引理取反,所有的存在和任意都反了过来。这就是开始说要注意存在和任意的原因。现在我们也发现,泵长度p不是没有用的。正过来时,p可以任意取值;但反过来说时,p就是任意取值了。泵长度p在证明泵引理时是完全没有用途的,因为它是一个存在的条件,可以任意取值;而在说明一个语言不是正则语言的时候,就要考虑泵长度p为任意值的情况了。
就考试而言,证明一个语言不是正则语言都是一个套路。因为要求证明的命题一定是正确的,所以我们可以无脑套入泵引理来导出矛盾反证。以经典的例子$B = \{0^n1^n|n\geq0\}$来说明一下证明语言不是正则语言的方法。
证明:
假设$B = \{0^n1^n|n\geq0\}$是正则语言。令p为泵长度。随便选择一个字符串$0^p1^p$,它属于B,且长度大于等于p。泵引理保证,它可以拆成3部分xyz,且满足之前的三个条件。由于$|xy|\leq p$,所以$xy$肯定全部由0组成。$xy^iz(i\geq0)$也一定属于B。但很明显,假设我把y重复100遍,由于y非空,xyz的前半部分一定出现了许许多多的0.这样的字符串是不属于B的,矛盾产生。因此,我们假设错误,B不是正则语言。
如果能仔细品味泵引理背后涉及的数学、逻辑原理,我相信人们都会被数学之美、思维之美所打动。这种美看不见摸不着,却深深埋藏在每个人脑中。对于那些爱思考的人来说,发现这些美,就能收获到一种无比的喜悦。能成为一名热爱自己的学科,并能在自己的学科里有所成就的科学家,真是一件令人羡慕的事情。可惜不是人人都适合科研,不是人人都有机遇把自己的一生都献给知识荒原的开拓。
总结一下。这一章讲的是正则语言,也就是可以被有限自动机识别的语言。这一章介绍了许多在后面都会介绍的概念:机器、状态、接收与拒绝、非确定性等。这些概念,是研究后面一些更强大的计算机器的基础。从全书的角度来看,这一章为后续的知识学习奠定了最低层次的基础。同时,这一章也围绕有限自动机,讲了许多实际的内容。有限自动机本身是最低级的计算机器,通过学习它我们能隐隐体会到计算的本质。
从考试的角度来看的话,这一章难点只有两个。一个是DFA向正则表达式的转换,一个是泵引理的理解与证明。而其他部分都不难。自动机名字看上去结构复杂,实际上就是一个有向图,哪怕不知道什么是图,会走迷宫,就能学会有限自动机的概念。非确定有限自动机的概念比较难理解,但一旦理解,一旦迈过那一道坎后,这个概念就会显得十分清晰。所有的证明都不会考,学习它们对于考试毫无益处。
后记
我写这篇文章的本意和之前复习概率论一样,是站在讲述者的角度来叙述这些知识,更好地把知识梳理清楚。从结果来看,复习效果是有,但是我花费了大量的时间,而且很多时间都花在了吹牛和一些我已经熟悉的知识的讲解上。而且,考虑到时间不是很够的原因,文章本身的质量也不够高,讲得也不够清楚。也就是说,我花了很多时间,就稍微复习了一些不太熟的知识,文章也没有写好来,总体上来看非常亏。我得到的结论是,复习还是不要写文章的好。如果想清楚地介绍一个知识,就在闲暇的时候慢慢地写文章;如果要复习,就用效率更高的方式来看书。这样复习的话,竹篮打水一场空,什么都没得到。