数独求解软件
Github链接
PSP耗时表
| PSP2.1 | Personal Software Process Stages | Expected time (min) | Actual time (min) |
|---|---|---|---|
| Planning | 计划 | 20 | 50 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 50 |
| Development | 开发 | 980 | 1119 |
| · Analysis | · 需求分析(包括学习新技术) | 50 | 120 |
| · Design Spec | · 生成设计文档 | 150 | 27 |
| · Design Review | · 设计复审(和同事审核设计文档) | - | - |
| · Coding Standard | · 代码规范(为目前的开发指定合适的规范) | 30 | 5 |
| · Design | · 具体设计 | 210 | 161 |
| · Coding | · 具体编码 | 300 | 575 |
| · Code Review | · 代码复审 | 60 | 25 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 180 | 206 |
| Reporting | 报告 | 170 | 100 |
| · Test Report | · 测试报告 | 80 | 60 |
| · Size Measurement | · 计算工作量 | 30 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结,并提出过程改进计划 | 60 | 30 |
| 合计 | 1170 | 1269 |
具体任务划分
- 开发 980
- 需求分析 50
- 列下任务的具体项 20
- 评估自己是否缺少相关知识,如果缺少则去收集资料 30
- 生成设计文档 150
- 用例模型、基本类图 30
- 动态模型设计 120
- 设计复审
- 代码规范 30
- 查现有代码规范 20
- 定义代码规范 10
- 具体设计 210
- 精化类图 60
- 精化动态模型 120
- 构件图 30
- 具体编码 300
- 代码复审 60
- 测试 180
- 单元测试 120
- 集成测试 60
- 需求分析 50
- 报告 170
- 测试报告 80
- 用例设计 20
- 测试 20
- 报告撰写 40
- 计算工作量 30
- 总结 60
- 测试报告 80
解题思路
需求分析
阅读作业要求文档后,我对需求的总结如下:
任务主要分两个部分:数独生成和数独求解。
数独生成要求通过可处理异常输入的命令行参数传入生成终局的数量,按照格式要求生成指定数量的终局。格式要求是数字用空格隔开,行末无空格,文件末无换行,终局间空一行。终局第一个数字为学号后两位之和模9加1。
数独求解要求从命令行读取待求解数独文件名,从文件中读取所有终局并按和数独生成同一格式输出求解结果。
由于数据求解需要数据,我还需要加入一个生成待求解的数独。参考附加任务的需求,待求解数独满足挖空数在30~60之间,每个宫不少于2个。
解法思考
数独终局生成
由于数独的每一行都是不重复的,因此每一行可以看成一个9个数的排列。一行一行地生成数独或许是一个比较好的方法。
数独的第一行就可以区别出一类数独。如果能得到一个终局的话,只需要修改第一行的映射,就能快速得到大量终局。同时,由于数独的限制比较强,搜索算法不会浪费很多时间在不合法终局上。如果知道了前几行,可以对剩下的部分进行dfs暴力搜索。这一步和数独求解完全相同,将在下一节分析。现在的问题就是如何生成前几行。
假设现在我们得到了第一行的一个合法排列。对于给定的一行,考虑有多少新行,使得新行和给定的行的三部分都能放在同一个宫里。这是一个排列组合的问题,我用分类讨论的方法对它进行了求解。
对于给定的行,行内的每个数只需要考虑它们来自哪个宫。不妨把给定的行表示为[1 1 1 2 2 2 3 3 3],新行表示为[0 0 0 0 0 0 0 0 0]。0表示未填,1、2、3表示这个数来自旧行的哪一个宫。我们先考虑位置信息,最后再区分三个1、2、3。
分类讨论1 1 1被怎么放到了新行。根据这三个数有几个放到了第二个宫、第三个宫,可分成四种情况:
1 | [0 0 0 0 0 0 1 1 1] |
类似地,可以分类讨论,把2、3填入第二行,使得第二行合法。通过排列组合的计算,总共能得出$C_3^3C_3^3+C_3^2C_3^2C_3^1+C_3^1C_3^1C_3^1+C_3^0C_3^0=56$种不同的结果。
这样分类的好处是,对于一个给定的第一行,每种生成的序列的不重复的。改变第一行的映射就能改变终局。而第一行由于第一个数固定,有$8!=40320$种可能。因此,用这种方法至少可以生成$56\times40320=2257920$种终局,这个数满足$10^6$的需求。
因此终局生成的算法总结如下:
固定第一行第一个数,随机生成一个排列
按上述方法枚举出第二行的所有可能,把对应的1、2、3转换成任意一个合法的序列。
使用求解方法得到一个终局。
交换数字映射来得到额外的终局。
如果仅仅要满足需求的话,最多只需要求解56个数独。如果要更多的终局的话,只需要在求解的时候多求几组解就行了。
数独求解
我在玩数独的时候发现了两个性质:某个宫的某个数字只能填入一个位置;某一个位置只能被填入一个数。
因此搜索时,可以加入下列策略:对于每个宫的每个数建立一个表,表示它的可选位置;对于每个位置建立一个候选数字表。如果数字的位置唯一或位置的候选数唯一,就填上这个数,更新所有的表。如果没有唯一的数,就选一个候选数最少的位置,尝试填入一个数字。如果某个数的可选位置为空或者某个位置的候选数字为空,就回溯,直到数独填完。
待求解数独生成
待求解数独要从终局中生成。根据需求,只需先随机总空数,再每个宫随机挖掉两个空,再随机挖空直至满足空格数即可。
设计实现过程
面向对象分析与设计
用例图
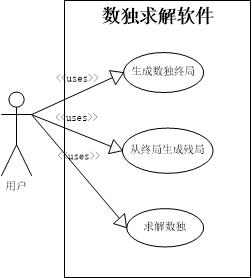
根据需求分析能够快速得到用例图。
基本类图
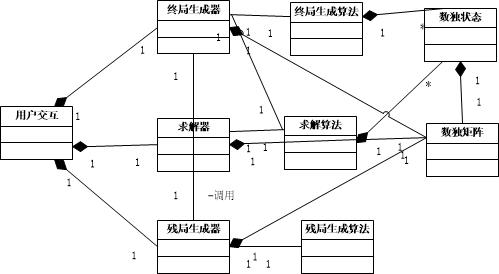
基本的类图建立如上。
用户交互类负责处理输入输出,并且根据输入参数来调用执行该任务的类。
为了使算法能够复用,每项任务的算法单独建立一个类。
数独矩阵只存储了数独81个数的信息,该类被所有的任务类使用。在终局生成算法和求解算法中,会用到数独的其他信息,这些附加信息用一个新的数独状态类来存储。
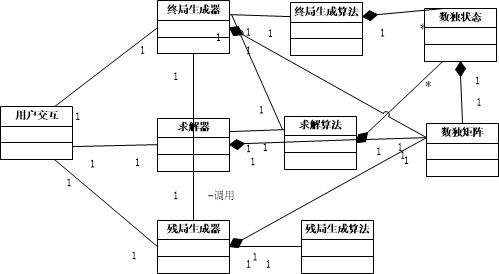
后来修改了一下类图的设计,三个任务器不应该做为用户交互类的子对象,应该是一种关联关系。
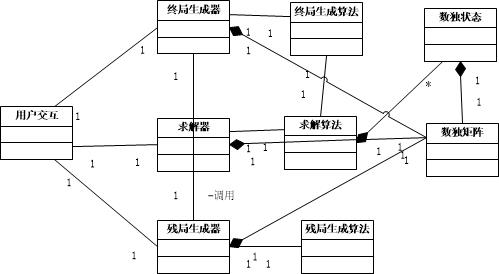
后来写终局生成算法的时候发现终局生成器和终局生成算法的关联设计得不太对。
(以上两个任务共花费27分钟)
活动图
数独求解
(花费40分钟)
根据之前分析问题时的算法,得到以下活动图:
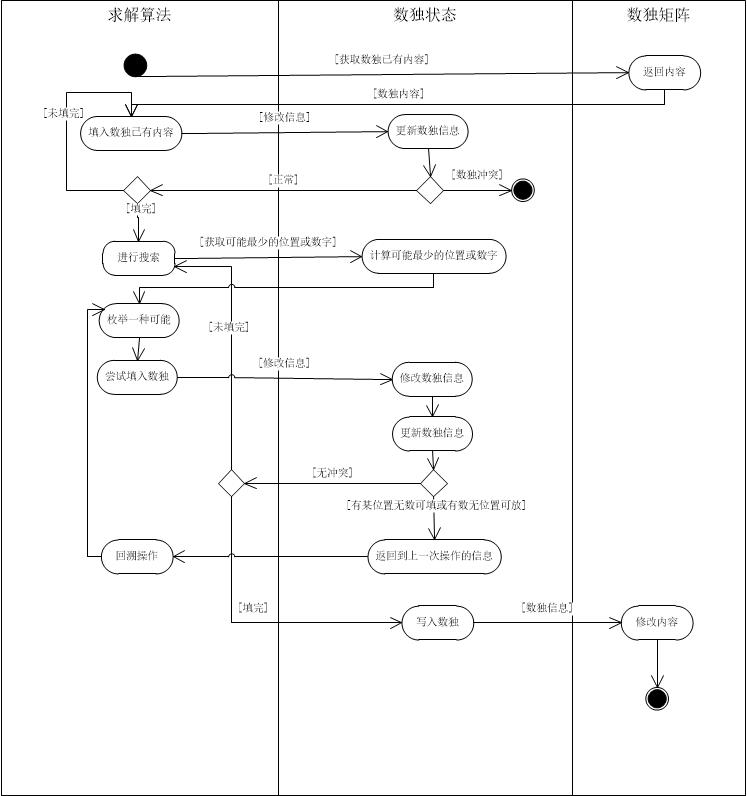
终局生成
根据之前分析问题时的算法,得到以下活动图:
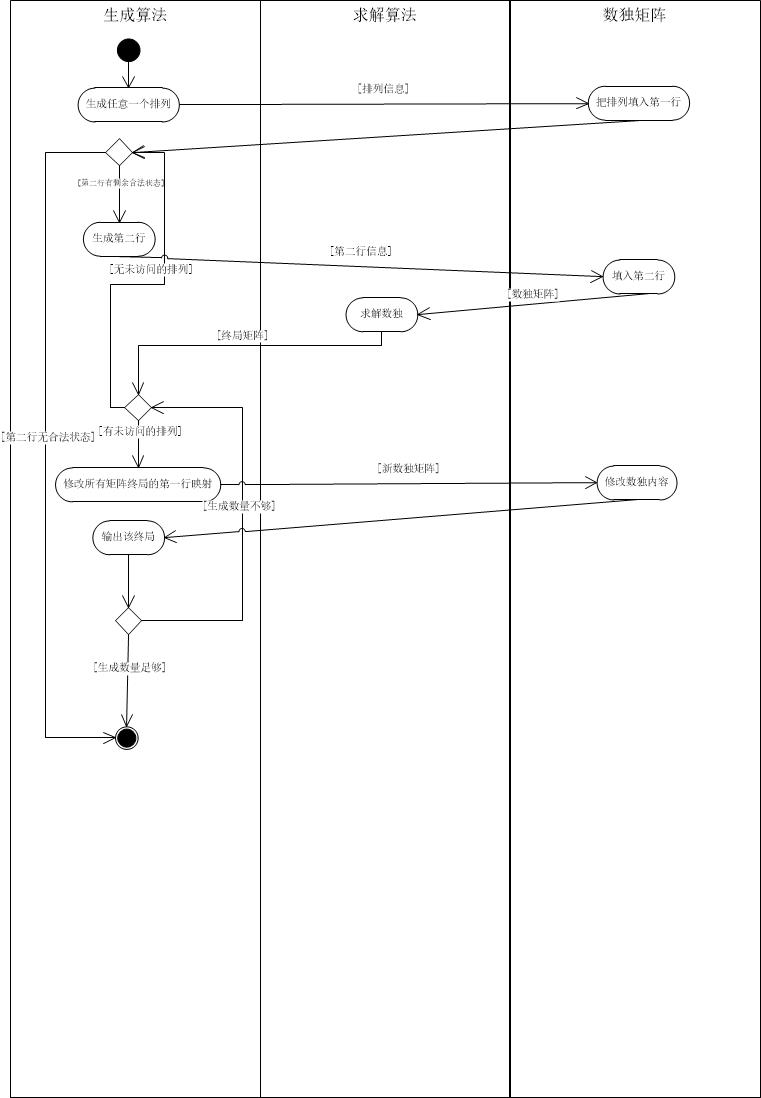
(花费24分钟)
精化类图
感觉visio建模很不方便,没有提供数组的定义。以下类图表示我在建类时的大致想法,与实际的类定义应该存在不小的出入。
数独矩阵

数独状态
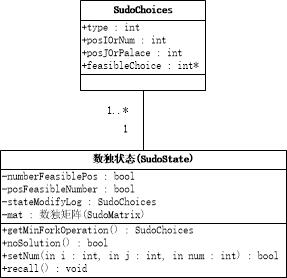
求解算法

(以上三个任务共花费38分钟)
生成算法

(花费5分钟)
残局生成算法

(花费5分钟)
终局生成器

求解器

残局生成器

(共花费14分钟)
用户交互
用户交互部分需要对数独矩阵进行输入输出。这一部分应该再用一个类来完成。
用户的命令行命令可以分成两个部分:命令和参数。应该有检查命令和执行对应命令的函数也应该分成两大部分。
执行命令的具体细节都交给对应的命令器完成。

(花费35分钟)
程序设计
(已花费1小时)
(又花费了2小时)
(又花费了1小时40分钟)
(又花费了40分钟)
(又花费了30分钟)
(又花费了45分钟)
(又花费了60分钟)
(优化花了120分钟)
求解算法
根据之前的面向对象分析与设计,我实现了4个类:SudoMatrix, SudoChoice, SudoState, SudoSolveAlgorithm。和设计的时候相比,每个类有一些变化。
SudoMatrix多写了很多方便调用的静态函数,比如位置坐标和第几个宫第几个数坐标的互相转换。
SudoChoice所有的操作都是封装好的,比如加入一个选项,去掉一个选项。
由于大致的结构都已经预先设计好了,代码实现得比较顺利,Debug时间很少。
最终求解算法定义如下:
1 | class SudoSolveAlgorithm |
算法只维护了一个变量:当前的数独状态。
算法主要函数solve实现如下:
1 | bool SudoSolveAlgorithm::solve(SudoMatrix& mat) |
和之前的活动图设计的一样,算法先把已有内容填充进数独矩阵中,之后进行dfs。如果有任意一个步骤中发现数独无解,就立刻返回false。如果数独成功求解出来,就把结果数独进行拷贝。
dfs只对数独当前状态这个变量进行操作。不断找可能最小的下一状态,如果碰到了无解的情况就让状态回溯。
终局生成算法
该类定义如下:
1 | class SudoGenerateAlgorithm |
和设计的时候相比,实现时又加了一个dfs函数,以搜索前两行的合法状态。
算法仅提供生成模板的函数和从模板和排列生成最终终局的函数。具体生成多个矩阵的工作在终局生成器中完成。
残局生成算法
该类定义如下:
1 | class SudoEndGameAlgorithm |
和设计的时候相比,算法的主要函数中多了一个参数,表示随机种子。
交互类与命令器
1 | class CmdInteraction |
交互类在最终实现的时候还是把每种命令器当成了子对象。
1 | class FinalStateGenerator |
终局生成器和设计的时候差不多,只有一个调用函数。做为输出的数组需要提前分配内存。根据需求,可以设置固定在第一行第一个的数字。
1 | class Solver |
求解器仅仅在求解算法上面加了一层调用,和设计时几乎一样。
1 | class EndGameGenerator |
残局生成器和设计时也差不多,只不过难度是用枚举表示的。对应生成算法,生成器也需要输入一个随机种子。
难度之间只有总空数和每个宫空数的不同。简单难度总空数20,每个宫至少2个空;中等难度总空数40,每个宫至少2个空;困难难度总空数60,每个宫至少3个空。
单元测试
由于VS2017 Community查看不了代码覆盖率,单元测试仅能测试代码的大致正确性。
终局生成器
由于生成器只有一个函数generateFinalState,我仅对这一个函数做了测试。
我测试了三个指标:生成的数独是否正确(满足行列宫不重)、第一个数是否正确、是否有重复的数独。
其中是否有重复的数独直接比较是O(n^2)的,测试起来十分慢。我把每个数独的每一行转换成一个数字,一整个数独就可以看成是一个9个数字的数组。我把每个数独转换成数独,扔到一个set里。如果在set发现了重复的数组,就说明有数独矩阵重复。这样测试重复的复杂度是O(nlogn)的。

如图,我总共运行了两次测试。两次测试只有生成数独的数量不同,一次是1000,一次是100000.
残局生成器
我用终局生成器生成了终局,之后把终局放入残局生成器了生成残局。
由于终局生成器已经验证过正确性,现在只对残局生成器验证两个指标:每个宫的最小空格数、所有空格数之和。
我对3种难度的残局生成器各设置了3个种子进行测试。生成数独的数量都是100个。
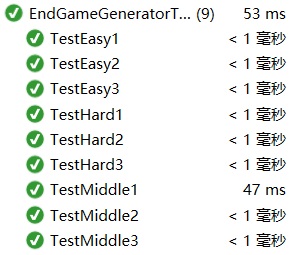
求解器
(测试求解算法正确性花费30分钟)

我在main函数里添加了一些临时代码,以验证求解算法的正确性和效率。
我在http://www.sudoku.name/index-cn.php 这个网站上随便找了一个难度为困难的数独,在Release模式下运行代码。从结果中可以看出,算法高效且正确的完成了任务。
最后我把残局生成器单元测试中得到的9组数据放入求解器进行测试,仅考虑求解出来的数独是否完全合法。
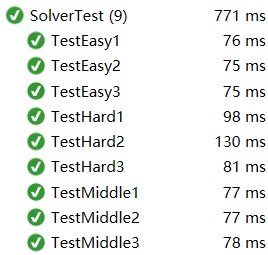
(之后共花了100分钟)
集成测试
我直接运行最终程序,做集成测试。
交互模块的测试用例可分成以下等价类:
命令个数错误
命令错误(无‘-’)
- 命令错误(有’-‘,第二个及后面的字符不对)
- 命令参数错误
命令参数错误根据具体的命令可以细分:
- -c 之后是字母
- -c 之后数字不合法
- -s 之后不是路径
- -s 之后文件不存在
我先对以上七种情况设计了10个测试用例,运行结果如下:
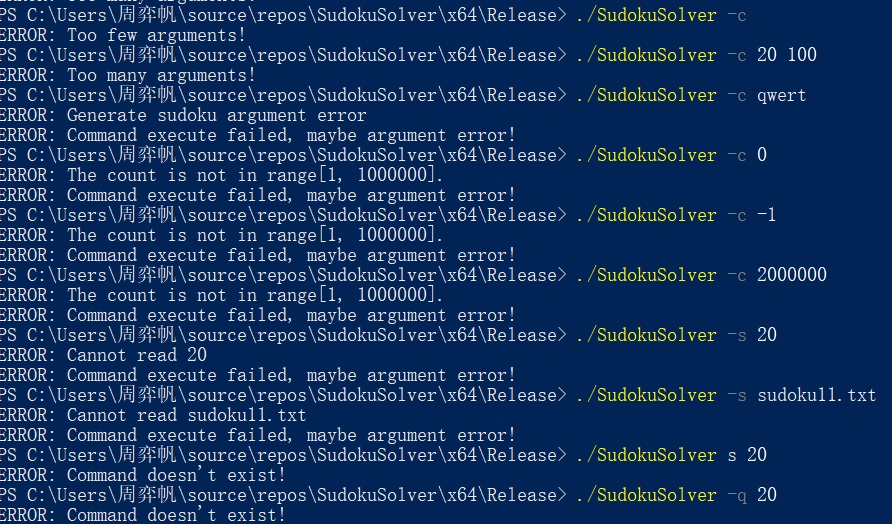
最后我输入了两个正确的命令。(sudokuInput.txt里有预先生成好的20个数独题目)

在集成测试的时候,我发现我输出的最后一行有空行。经过修改后这个BUG被排除了。
(花费56分钟)
代码复审
我在VS中启用了代码分析,规则集为Mircrosoft本机建议规则。
一开始,有很多警告:

经过修改,警告被改掉了。
比较特殊的是一个和迭代器有关的警告。迭代器的偏移量我提前计算好不会报错,如果直接把偏移量的计算式和迭代器放到一起运算就会报错。这个可能和64位平台有关的警告我没有太理解。
(花费25分钟)
性能分析及程序优化
数独生成
性能分析结果
使用vs自带的性能分析,生成1000000个数独,得到的结果如下:
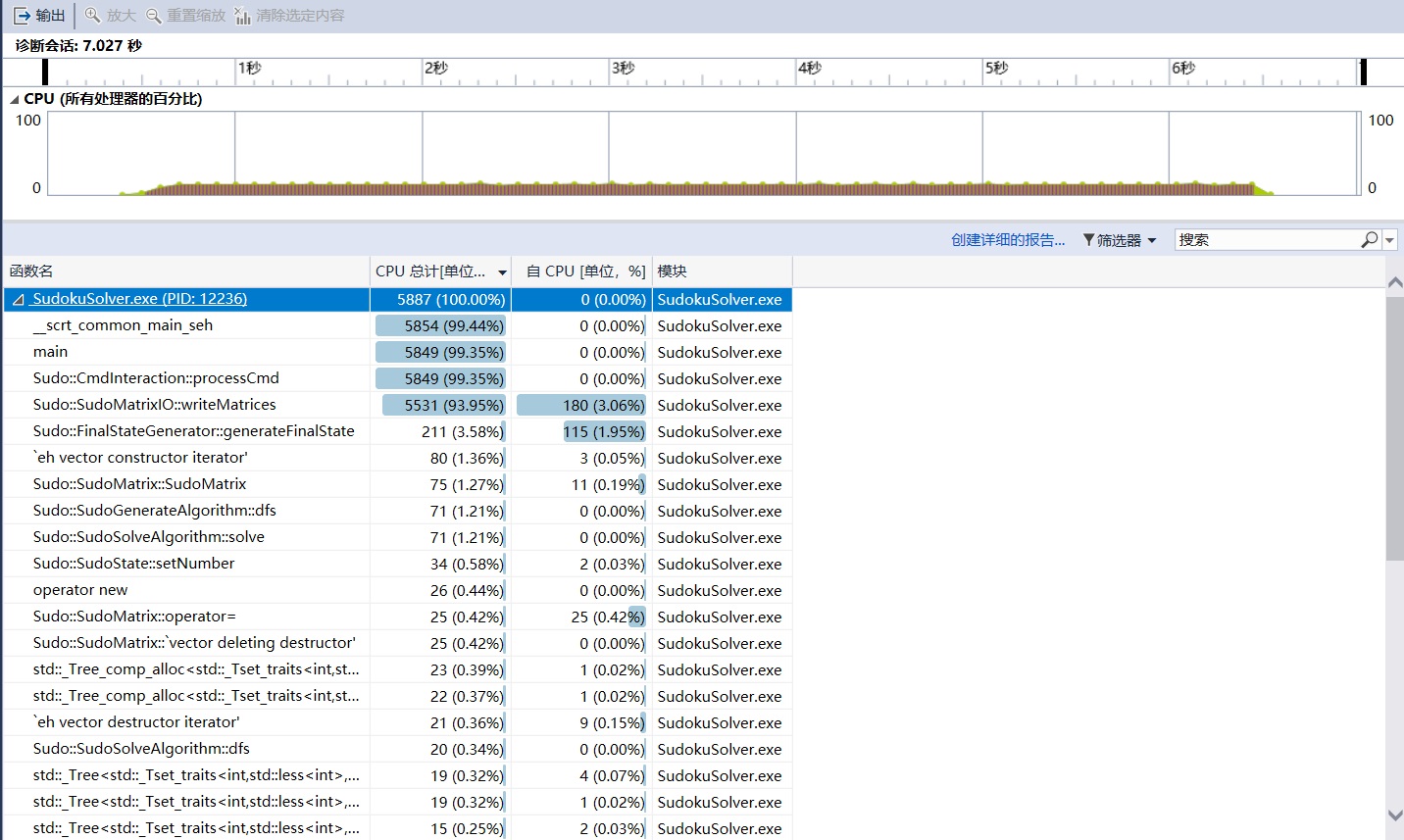
可以发现,主要的时间都花在输入上。
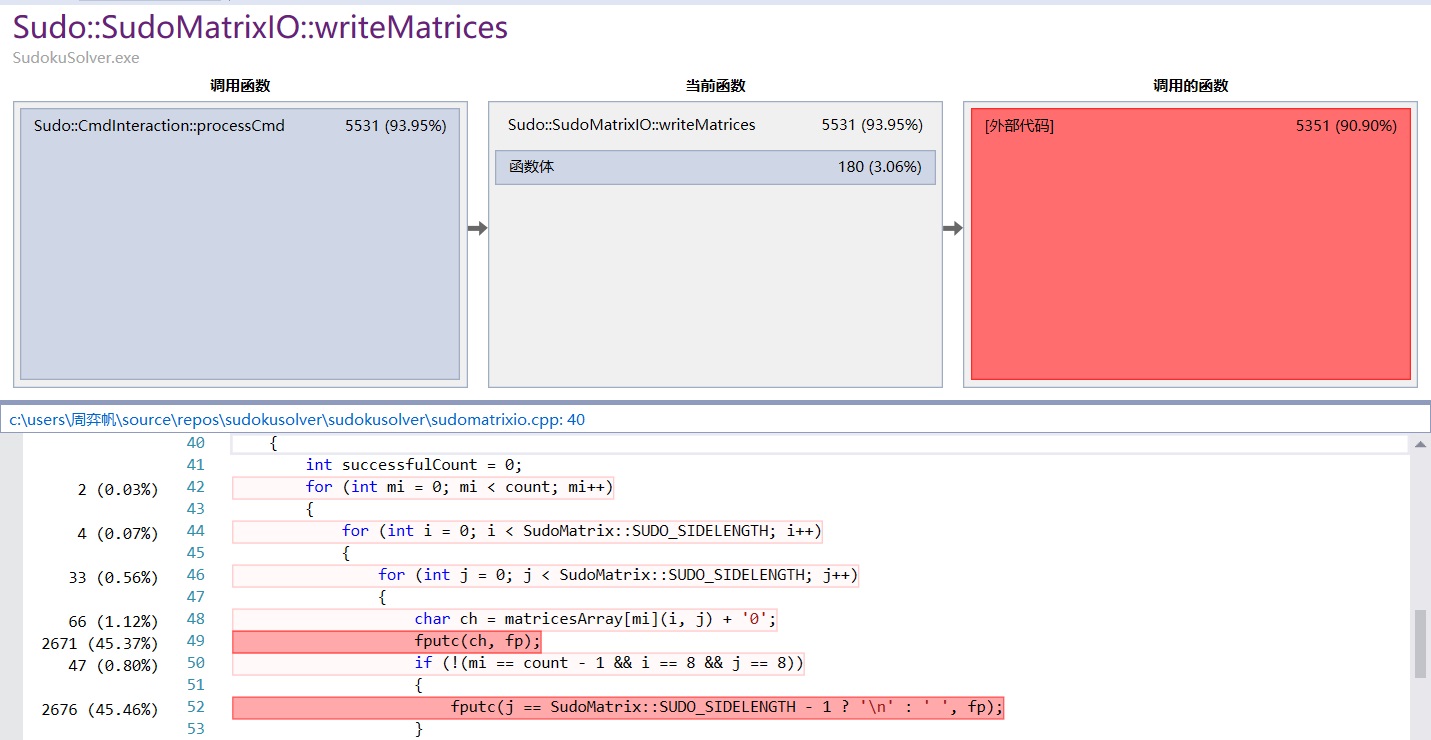
其中,最花时间的是fputc函数。
优化方法及结果
我把输出的字符先存到一个缓冲区里,每存100个矩阵的信息就输出一次。
输出一次性用fwrite输出。
另外,由于生成算法需要的模板较少,我直接把最终的模板放进了文件里面,而不是每次都计算模板。
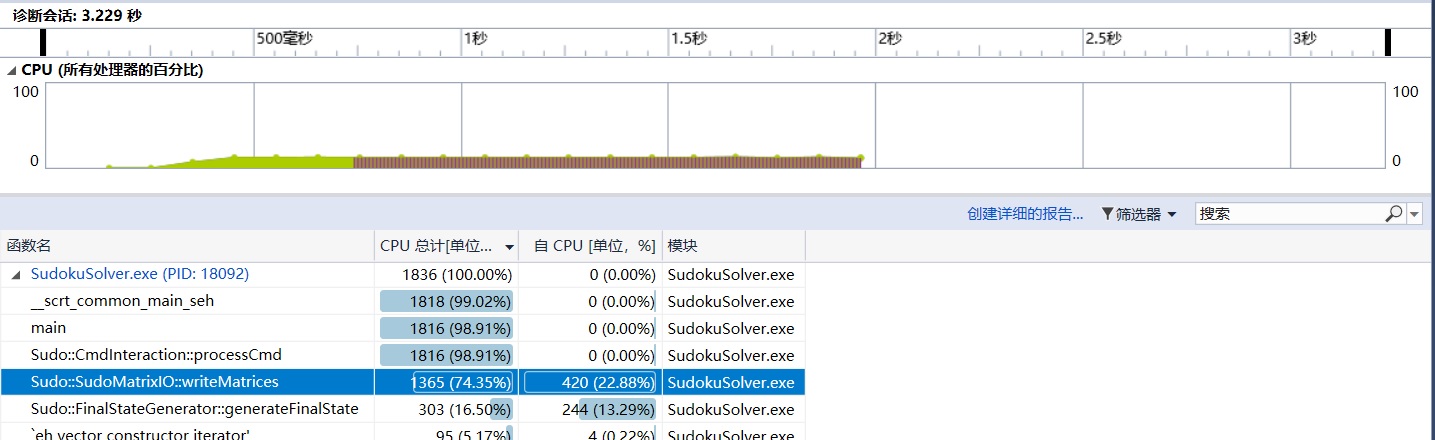
从结果可以看出,运行效率有所提升。
数独求解
初次结果
最开始的时候,求解1000000个数独的速度非常慢。我没有等程序跑完就关掉了程序。
优化方法及结果
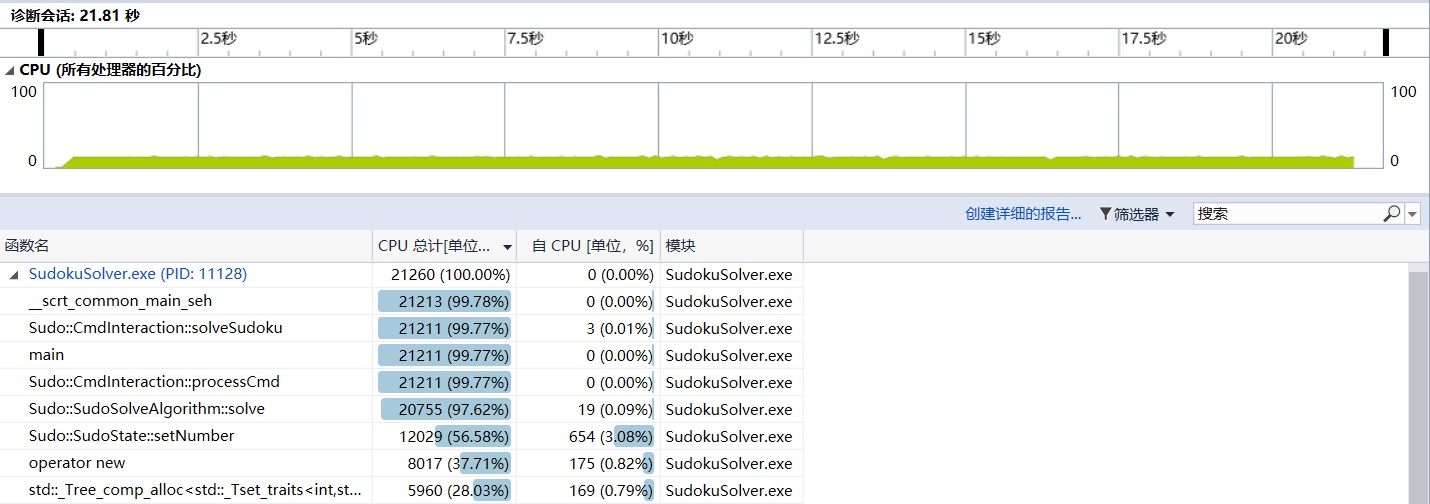
我用性能分析工具检查,发现很多时间都浪费在了数据结构操作上。
我把存状态的set改成了bitset,把部分操作改成了位询问、修改。
同时,我稍微优化了状态初始化部分的算法。在初始化一个数独的时候,不会再写入修改日志了。
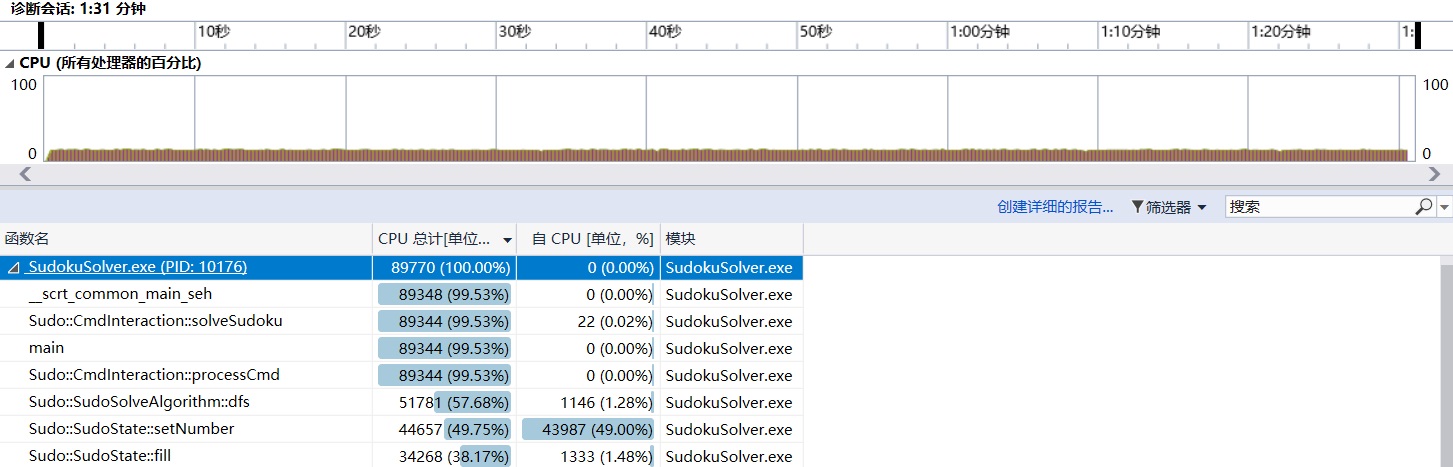
现在程序能90秒跑完了。
单元测试

经过一些修改后,单元测试又能通过了。
最终程序代码说明
求解算法
1 | bool SudoSolveAlgorithm::solve(SudoMatrix& mat) |
求解算法是整个软件的核心。在求解时,算法先更新当前已知的信息,之后对其他部分做DFS。
1 | bool SudoState::fill(const SudoMatrix& mat) |
FillState会调用SudoState::fill函数。该函数先初始化整体的信息:当前已经运行到第几步,当前的数独矩阵。并且把每个位置的候选数和每个数字在每个宫的侯选位置初始化。最后,对于每个已经存在的数,用setNumber()填入并更新状态。
1 | bool SudoSolveAlgorithm::dfs() |
dfs函数是用于搜索解的函数。该函数每次从数独当前状态中获得候选情况最少的位置或数字,之后对这个地方进行搜索。搜索完全部解就会返回成功;setNumber返回false说明搜索失败,数独当前状态会进行回溯。
1 | bool SudoState::setNumber(int i, int j, int num, bool recordLog) |
数独状态的setNumber函数是算法中的十分重要的函数。该函数在填入一个数字后,更新相关行、列、宫的候选数字信息及每个数的候选位置信息。同时,这一步的操作会被记录下来,以进行回溯。
生成算法
在模板是本地储存而不是实时计算后,生成算法只剩了从排列构造这一项任务。
1 | SudoMatrix SudoGenerateAlgorithm::getSudokuFromPermutation(std::vector<int>& permutation, int templateId) |
生成算法类提供了排列构造的函数。
1 | int FinalStateGenerator::generateFinalState(int count, Sudo::SudoMatrix* matrixArr, int fixFirstNumber) const |
按照需求生成数独的工作交给生成器来完成。生成器生成许多固定第一个数字的排列,利用排列生成数独,直到生成的数独满足数量要求为止。
心得体会
从我对整个项目的评价和我学到的东西两个方面来谈我的体会。
我对项目的评价可以分成我的开发时间管理评价和项目结果评价。我这次时间管理得非常不好。我一开始觉得这个项目难度较低,花费不了什么时间。我很早就想好整个项目的框架和具体算法,设计和编码的过程也还算顺利。但我错估了测试和项目优化的时间,项目后期的时间非常紧,我也没来得及完成附加题。
项目完成得也不够好。我在设计数独状态类的时候没有设计好,返回给数独求解类的信息和数独状态类自己保存的信息应该分成两个类。我在后来代码优化的时候由于这两个类没有分开,碰到了一些麻烦。项目的性能还存在优化的空间,求解算法可以进一步压缩时间。
在这个项目中,我学习到了一些工具的使用方法、软件工程知识、软件工程实践经历。我学会了VS单元测试工具、性能分析工具、代码分析工具的使用。我在画用例图、类图等UML图的过程中对于软件工程的理解进一步加深。在本次项目中,我不局限于编码,而是完成了整个软件的开发流程,体会到了软件开发的不易。
我本身就有比较多的大型程序开发经验。在学过了软件工程课并经历了这次的开发过程后,我能把知识和我的经验结合起来,以后写出模块划分得更好、测试做得更全面、文档更完整的软件。
更新记录
19.12.24 11:36
- 添加博客地址。
- 完成PSP耗时表。
19.12.27 12:03
- 分析题意,想出算法。
19.12.28 23:03
- 设计用例图。
- 设计基本类图。
20.1.1 21:41
项目进展
- 画完求解活动图。
- 精化求解模块的类图。
- 求解模块的程序设计中。
项目更新
- 修改基本类图。
博客进展
- 博客跟进项目进展。
- 添加未来任务的大标题。
20.1.2 16:30
- 项目进展
- 求解模块的程序设计中。
- 博客进展
- 记录了花费在程序上的时间。
- 项目进展
20.1.10 15:48
- 项目进展
- 完成求解算法。
- 求解算法基本测试完毕。
- 博客进展
- 更新了求解算法的代码简要说明。
- 更新了程序设计花费时间。
- 更新了求解算法的正确性测试结果。
- 项目进展
20.1.15 23:30
- 博客进展
- 添加了终局生成的活动图。
- 博客进展
2020.1.16 20.39
- 项目进展
- 设计并完成了终局生成算法模块。
- 给SudoMatrix类增加比较函数与复制函数。
- 博客进展
- 再次修改了基本类图。
- 添加了终局生成算法类图。
- 项目进展
2020.1.17 10:35
- 项目进展
- 设计并完成残局生成算法模块。
- 博客进展
- 添加了残局生成算法类图。
- 项目进展
2020.1.17 15:10
- 项目进展
- 设计并完成终局生成器、残局生成器、求解器、用户交互、数独矩阵IO类,但没有测试。
- 博客进展
- 添加项目进展中的设计类图。
- 项目进展
2020.1.18 21:26
- 项目进展
- 添加了单元测试的所有代码。
- 博客进展
- 统计了设计文档、具体设计、编码的时间。
- 更新了单元测试有关内容。
- 项目进展
2020.1.18 22:33
- 项目进展
- 完成集成测试的BUG修改。
- 博客进展
- 更新集成测试有关内容。
- 项目进展
2020.1.19 10:52
- 项目进展
- 完成代码复审
- 进行优化的分析
- 完成优化及优化后的测试
- 发布最终版本
- 博客进展
- 更新代码复审内容
- 更新优化内容
- 更新最终代码说明
- 项目进展
2020.1.19 21:14
- 博客进展
- 完成了心得体会。
- 博客进展