吴恩达《深度学习专项》笔记+代码实战（五）：深度学习的实践层面

学习提示

第二门课的知识点比较分散，开始展示每周的笔记之前，我会先梳理一下每周涉及的知识。

这一周会先介绍改进机器学习模型的基本方法。为了介绍这项知识，我们会学习两个新的概念：数据集的划分、偏差与方差问题。知道这两个概念后，我们就能够诊断当前机器学习模型存在的问题，进而找出改进的方法。

之后，我们会针对“高方差问题”，学习一系列解决此问题的方法。这些方法成为“正则化方法”。这周介绍的正则化方法有：添加正则化项、dropout、数据增强、提前停止。

最后，我们会学习几项和神经网络相关的技术。我们会学习用于加速训练的输入归一化，用于防止梯度计算出现问题的参数带权初始化，以及用于程序调试的梯度检查。

课堂笔记

数据集的划分：训练集/开发集/测试集

在使用机器学习的数据集时，我们一般把数据集分成三份：训练集、开发集、测试集。

机器学习是比深度学习的父集，表示一个更大的人工智能算法的集合。

开发集（Development Set）另一种常见的称呼是验证集(Validation Set)，即保留交叉验证（Hold-out Cross Validation)。

三种数据集的定义

它们三者的区别如下：

	训练集	开发集	测试集
用于优化参数	是	否	否
训练时可见？	是	是	否
最终测试时可见？	是	是	是

训练集就是令模型去拟合的数据。对于神经网络来说，我们把某类数据集输入进网络，之后用反向传播来优化网络的参数。这个过程中用的数据集就是训练集。

开发集是我们在训练时调整超参数时用到的数据集。我们会测试不同的超参数，看看模型在开发集上的性能，并选择令模型在开发集上最优的一组超参数。

测试集是我们最终用来评估模型的数据集。当模型在测试集上评测时，我们的模型已经不允许修改了。我们一般把模型在测试集上的评测结果作为模型的性能评估标准。

在我们之前实现的小猫分类项目中，准确来说，我们使用的不叫测试集，而叫做开发集，因为我们是根据那个”testing set”优化网络超参数的。

有人把训练集比作上课，开发集比作作业，测试集比作考试。如果你理解了这三个数据集的原理，会发现这个比喻还是挺贴切的。事实上，由于测试集不参与训练，一个机器学习项目可以没有测试集，就像我们哪怕不经过考试，也可以学到知识一样。

人们很容易混淆开发集/测试集。很多论文甚至把开发集作为最终的性能评估结果。但是很多时候审稿人对这些细节并不在意。作为有操守的研究者，应该严肃地区分开发集与测试集。

通过划分数据得到训练/测试集

在前一个机器学习纪元，人们通常会拿到一批数据，按7:3的比例划分训练集/测试集（对于没有超参数要调的模型），或者按6:2:2的比例划分训练集/开发集/测试集。

而在深度学习时代，数据量大大增加。实际上，开发集和测试集的目的都是评估模型，而评估模型所需的数据没有训练需要得那么多。所以，当整体的数据规模达到百万级，甚至更多时，我们只需要各取10000组数据作为开发集和测试集即可。

收集来自不同分布的数据集

除了从同一批数据中划分出不同的数据集，还有另一种得到训练集、测试集的方式——从不同分布中收集数据集。

分布是统计学里的概念，这里可以理解成不同来源，内容的“平均值”差别很大的数据。

比如，假如我们要为某个小猫分类器收集小猫的图片，我们的训练图片可以是来自互联网，而开发和验证的数据来自用户用收集拍摄的图片。

注意，由于开发集和验证集都是用来评估的，它们应该来自同一个分布。

偏差与方差

机器学习中，我们的模型会出现高偏差或/和高误差的问题。我们需要设法判断我们的模型是否有这些问题。

偏差(bias)与方差(variance)是统计学里的概念，前者表示一组数据离期待的平均值的差距，后者表示数据的离散程度。

试想一个射击运动员在打靶。偏差与打靶的总分数有关，因为总分越高，意味着每次射击都很靠近靶心；方差与选手的发挥稳定性有关，比如一个不稳定的选手可能一次9环，一次6环。

高偏差意味着模型总是不能得到很好的结果，高方差意味着模型不能很好地在所有数据集上取得好的结果（即只能在某些特定数据集上表现较好，在其他数据集上都表现较差）。

我们把高偏差的情况叫做“欠拟合”（可能模型还没有训练完，所以表现不够好），把高方差的情况叫做“过拟合”（模型在训练集上训练过头了，结果模型只能在训练集上有很好的表现，在其他数据集上表现偶读不好）。

让我们看课件里的一个点集分类的例子：

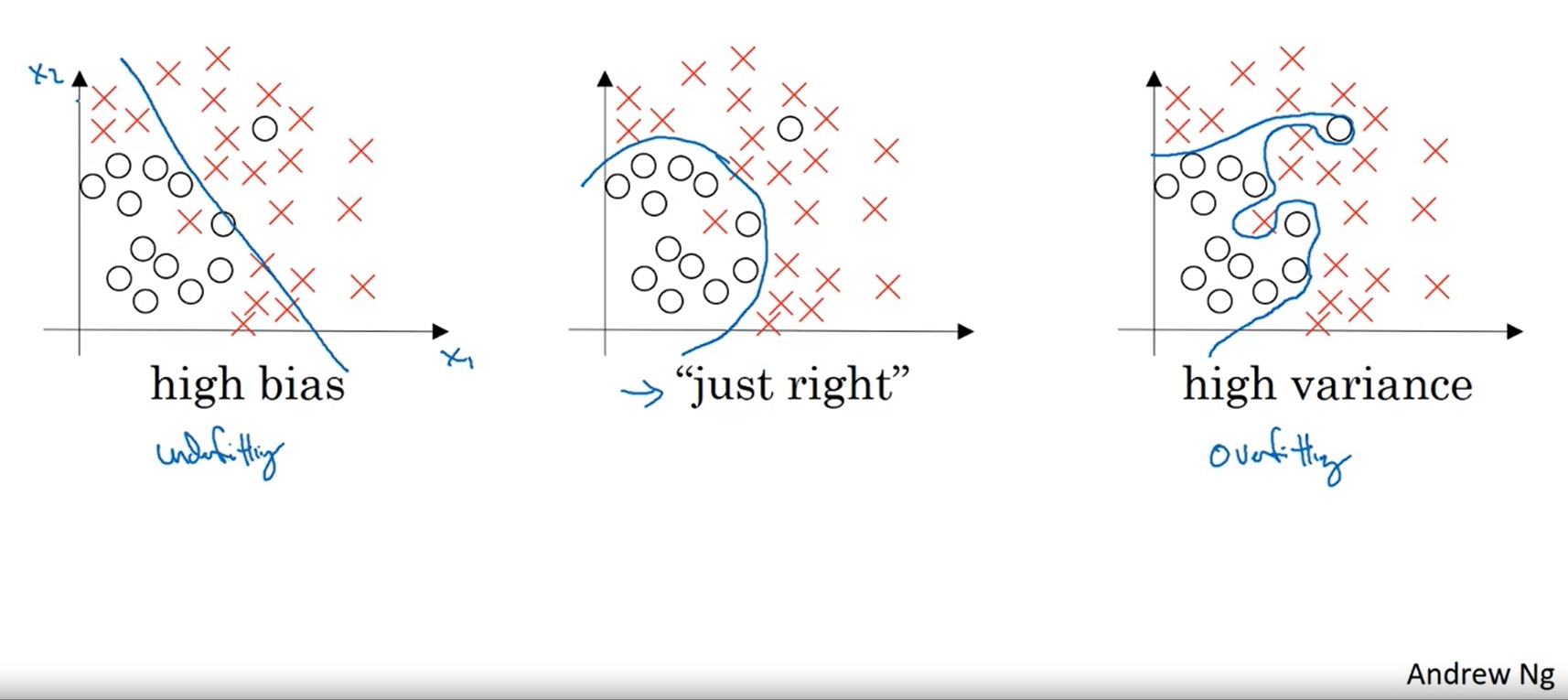
上图显示了欠拟合、“恰好”、过拟合这三种情况。

对于欠拟合的情况来说，一条直线并不足以把两类点分开，这个模型的整体表现较差。

对于过拟合的情况来说，模型过分追求训练集上的正确，结果产生了一条很奇怪的曲线。由于训练数据是有噪声（数据的标签不完全正确）的，这样的模型在真正的测试上可能表现不佳。

让我们人类来划分的话，最有可能给出的是中间那种划分结果。在这个模型中，虽然有些训练集中的点划分错了，但我们会认为这个模型在绝大多数数据上更合适。当我们用更多的测试数据来测试这个模型时，中间那幅图的测试结果肯定是这三种中最好的。

要判断机器学习模型是否存在高偏差或高方差的现象，可以去观察模型的训练集误差和开发集误差。以下是一个判断示例：

情况	1	2	3	4
训练集误差	1%	15%	0.5%	15%
开发集误差	11%	16%	1%	30%
诊断结果	高方差	高偏差	低误差、低方差	高误差、高方差

也就是说，如果开发集和训练集的表现差很多，就说明是高方差；如果训练集上的表现都很差，就是高偏差。

上面这些结论建立在最优误差——贝叶斯误差(Beyas Error)是0%的基础上下的判断。很多时候，仅通过输入数据中的信息，是不足以下判断的。比如告诉一个人是长头发，虽然这个人大概率是女生，但我们没有100%的把握说这是女生。如果我们知道人群中留长发的90%是女生，10%是男生，那么在这个“长头发分辨性别”的任务里的贝叶斯误差就是10%。

假如上面那个任务的贝叶斯误差是15%，那么我们认为情况2也是一个低误差的情况，因为它几乎做到了最优的准确率。

改进机器学习的基本方法

通过上一节介绍的看训练误差、测试误差的方式，我们能够诊断出我们的模型当前是否存在高偏差或高误差的问题。这一节我们来讨论如何解决这些问题。

首先检查高偏差问题。如果模型存在高偏差，则应该尝试使用更复杂的网络、更多增加训练时间。

确保模型没有高偏差问题后，才应该开始检查模型的方差。如果模型存在高方差，则应该增加数据或使用正则化。

此外，使用更合理的网络架构，往往对降低误差和方差都有效。

正则化 (Regularization)

其实正则化的意思就是“为防止过拟合而添加额外信息的过程”。在机器学习中，一种正则化方法是给损失函数添加一些与参数有关的额外项，以调整参数在梯度下降中的更新过程。正则化的数学原理我们会在下一节里学习，这一节先认识一下正则化是怎么操作的。

先看一下，对于简单的逻辑回归，我们应该怎么加正则化项。

原来，逻辑回归的损失函数是:

$$J(w, b) = \frac{1}{m}\Sigma_{i=1}^{m}L(\hat{y}, y)$$

现在我们给它加一个和参数$w$有关的项

$$J(w, b) = \frac{1}{m}\Sigma_{i=1}^{m}L(\hat{y}, y) + \frac{\lambda}{2m}||w^2||_2$$

最右边那个 $\frac{\lambda}{2m}||w||^2_2$ 就是额外加进来的正则项。其中$\lambda$是一个可调的超参数，$||w||^2_2$表示计算向量$w$的l2范数，即:

$$||w||^2_2 = \Sigma_{j=1}^{n_x}w_j^2$$

也就是说，某向量的l2范数就是它所有分量平方再求和。

类似地，其实向量也有1范数，也可以用来做正则化：

$$||w||_1 = \Sigma_{j=1}^{n_x}|w_j|$$

1范数就是向量所有分量取绝对值再求和。

使用1范数做正则化会导致参数中出现很多0。人们还是倾向使用l2范数做正则化。

看到这里，大家或许会有问题：$b$也是逻辑回归的参数，为什么$w$有正则项，$b$就没有？实际上，要给$b$加正则项也可以。但是在大多数情况下，参数$w$的数量远多于$b$, 和$b$相关的正则项几乎不会影响到最终的损失函数。为了让整个过程更简洁一些，$b$的正则项就被省略了。（其实就是程序员们偷懒了，顺便让计算机也偷个懒）

当情况推广到神经网络时，添加正则项的方法是类似的，只不过参数$W$变成了矩阵而已。对应的正则项如下：

$$\frac{\lambda}{2m}\Sigma_{l=1}^{L}||W^{[l]}||_F^2$$

其中,

$$||W^{[l]}||_F^2 = \Sigma_{i=1}^{n^{[l]}}\Sigma_{j=1}^{n^{[l-1]}}(W_{ij}^{[l]})^2$$

这种矩阵范数叫做Frobenius范数，叫它F-范数就行了。

如之前的文章所述，对于梯度下降算法来说，定义损失函数的根本目的是为了对参数求导。当参数$W$在损失函数里多了一项后，它的导数会有怎样的变化呢？

对于某参数向量$w$来说，其实它的导数就多了一项：

$$\begin{align*} & (\frac{\lambda}{2m}w^2)' \\ =& \frac{\lambda}{m}w \end{align*}$$

大家知道为什么正则项分母里有一个2了吗？没错，这是为了让求出来的导数更简洁一点。反正有超参数$\lambda$，分母多个2少个2没有任何区别。

最终，参数向量$w$会按如下的方式更新：

$$\begin{align*} w &:= w - \alpha (dw +\frac{\lambda}{m}w) \\ \Rightarrow w &:=(1-\frac{\alpha\lambda}{m})w-\alpha dw \end{align*}$$

仔细一看，其实相较之前的梯度更新公式，只是$w$的系数从$1$变成了$1-\frac{\alpha\lambda}{m}$。因此，用l2范数做正则化的方法会被称为 “权重衰减(Weight Decay)” ,$\lambda$在某些编程框架中直接就被叫做weight decay。

为什么正则项能减少方差

回忆前面见过的“高方差”的拟合曲线：

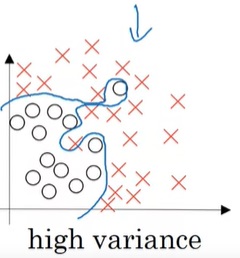
这个曲线之所以能够那么精确地过拟合，是因为这个曲线的参数过多。如果这个曲线的参数少一点，那么它就不会有那么复杂的形状，过拟合现象也会得到缓解。

也就是说，如果神经网络简单一点，每个参数对网络的影响小一点，那么网络就更难去过拟合那些极端的数据。

添加了正则项后，网络的参数都受到了一定的“惩罚”。因此，参数会倾向于变得更小，从而产生刚刚提到的减轻过拟合的效果。

Dropout (失活)

Dropout 怎么翻译都不好听，直接保持英文吧。

还有一种常用的正则化方法叫做 dropout，即随机使神经网络中的一些神经元“失活”。如下图所示：

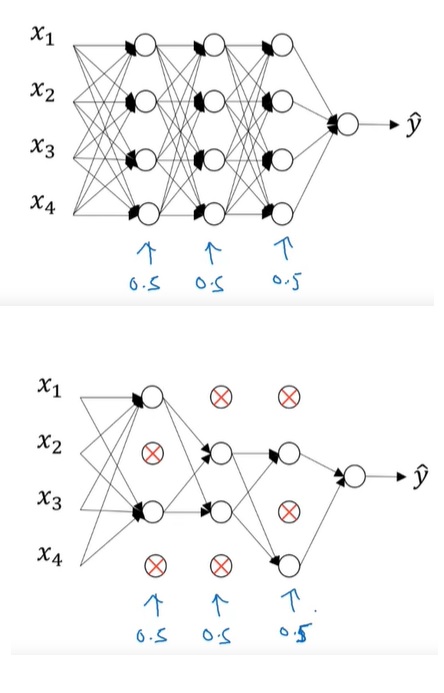
我们可以令所有神经元在每轮训练中有50%的几率失活。在某轮训练中，神经网络的失活情况可能会像上图中下半部分所示：那些打叉的神经元不参与计算和，整个神经网络变得简单了许多。

在实现时，我们常常使用一种叫做”Inverted dropout”的实现方法。Inverted dropout 的思想是：对于神经网络的每一层，生成一个表示有哪些神经元失活的“失活矩阵”，再用这个矩阵去乘上这一层的激活输出（做乘法即令没有失效的激活保持原值，失效的激活取0）

其实现代码如下：

d = np.random.rand(a.shape[0], a.shape[1]) < keep_prob
a = a * d
a /= keep_prob

这段代码中，d是失活矩阵。该矩阵通过一个随机数矩阵和一个保留概率keep_prob做小于运算生成。np.random.rand可以生成一个矩阵，其中矩阵中每个数都会均匀地随机出现在0~1之间。这样，每个数小于keep_prob的概率都是keep_prob。比如keep_prob=0.8,那么每个神经元都有80%的几率得到保留，20%的几率被丢弃。

做完小于运算后，d其实是一个bool值矩阵。拿bool矩阵和一个普通矩阵做逐对乘法，就等于bool矩阵为True的地方取普通矩阵的原值，bool矩阵为False的地方取0。

最后，得到了丢弃掉某些神经元的激活输出a后，我们还要做一个操作a /= keep_prob。可以想象，如果我们丢掉了一些神经元，那么整个激活输出的“总和”的期望会变小。比如keep_prob为0.8，那么整个输出的大小都近似会变为原来的0.8倍。为了让输出的期望不变，我们要把激活输出除以keep_prob。

如前文所强调的，dropout一次是对一层而言的。也就是说，每一层可以有不同的keep_prob。

dropout可能对损失函数变化曲线产生影响。一般调试时，如果损失函数一直在降，就说明训练算法没什么问题。但是，加入dropout后，由于每次优化的参数不太一样了，损失函数可能不会单调递减。因此，为了调试神经网络，可以先关闭dropout。确定损失函数确实在下降后，再开启它。

由于在CV（计算机视觉）中，图像的输入规模都很大，数据不足而引起过拟合是一件常见的事。因此，dropout在CV中被广泛应用。

注意，dropout是一种训练策略。在测试的时候，不需要使用dropout。

和刚才一样，我们再来探讨一下为什么dropout能够生效。有了dropout，意味着神经网络的权重不能集中在部分神经元上，因为某个神经元随时都可能会失效。因此，神经网络的权重会更加平均。更加平均，意味着计算参数平方的l2范数会更小。也就是说，dropout令参数更平均，起到了和刚刚添加l2正则类似的效果。

其他正则化方法

1. 数据增强

比如对于一幅图片，我们可以翻转、旋转、缩进，以生成“更多”的训练数据。

1. 提前停止 (early stopping)

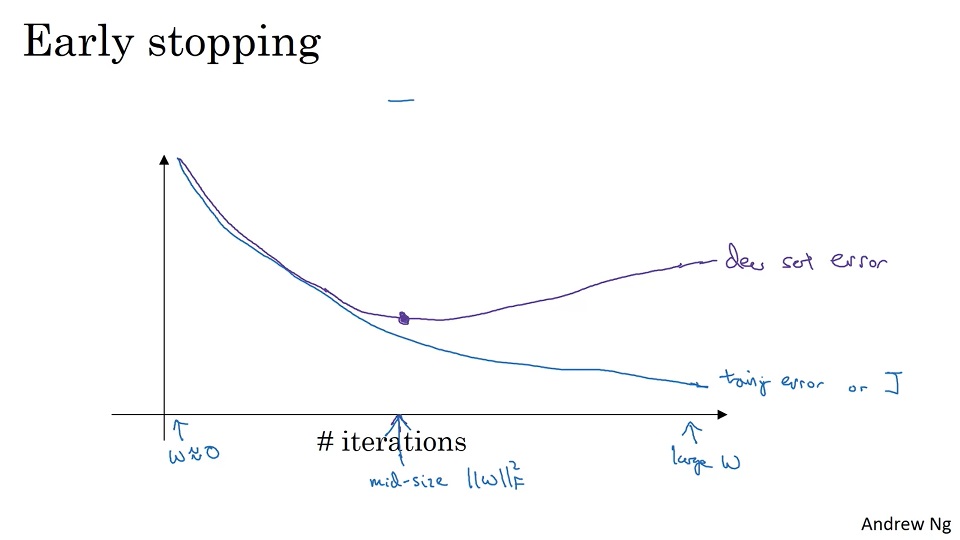
随着训练的进行，网络的损失函数可能越来越小，但开发集上的精度会越来越高。只是因为训练得越久，参数就会越来越大，即越来越倾向于过拟合。提早结束训练，能够让参数取到一个合适的值。

提前中止也有一些不好的地方。在机器学习中，训练模型可以分成两部分：让损失函数更小、防止模型过拟合。我们通常会对这两部分独立地进行优化，即控制优化方法不变，改变正则化方法；或者改变减小梯度的算法，保证模型不进行任何正则化操作。而提前中止实际上混淆了减小损失函数和防止模型过拟合这两件事，不利于采取更多的调试策略。

独立地看待问题的两个变量，这种方法叫做 “正交化”。这种控制变量的思想在科研、编程，甚至是处理人生中各种各样的问题时都很适用。

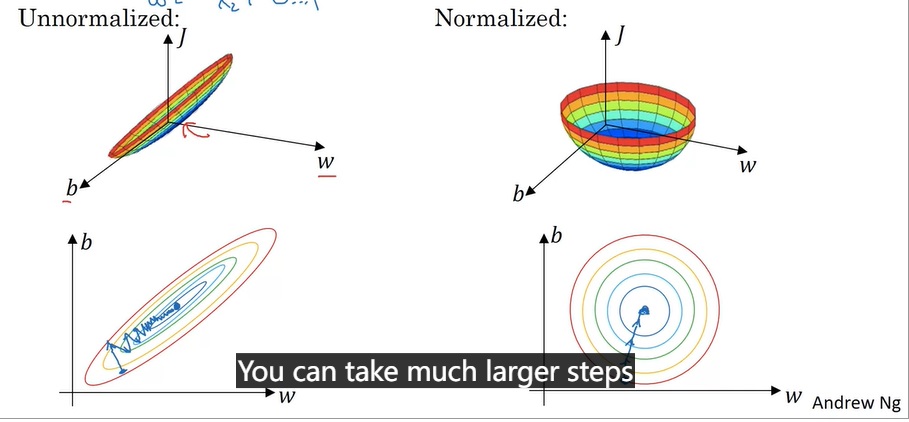
输入归一化(Normalization)

参考网上的翻译，我把 Normalization 翻译为归一化，Standardization 翻译成标准化。其实这两个中文翻译经常会混着用，翻译上的区别不用太在意。

我们应该尽可能让输入向量的每一个分量都满足标准正态分布。如果你对数学不熟，我们可以来看一个例子:

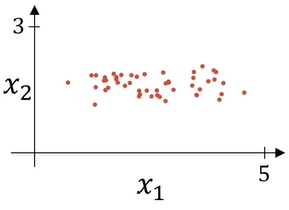
假设我们每个输出张量长度为2，即有两个分量:$x_1, x_2$。我们可以认为每个输入向量就是一个二维平面上的点。统计完了所有样本，我们或许可以发现所有样本的$x_1$位于[0, 5]这个区间，$x_2$位于[0, 3]这个区间，两个区间长度不一。而且，数据在$x_1$上比较分散,$x_2$上比较靠拢。这个训练样本显得非常凌乱。

如果我们让输入归一化，使输入向量的每一个分量都满足了正态分布，难么这些数据可能会长得这样:

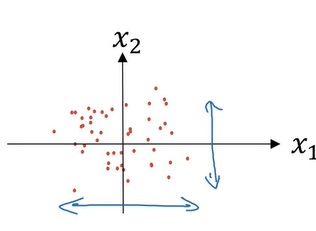
这样，数据分布的区间不仅长度相同，而且离散的程度也相同了。

归一化可以通过以下方式实现：

$$\mu=\frac{1}{m}\Sigma_{i=1}^{m}x^{(i)} \\ x := (x - \mu) \\ \sigma^2=\frac{1}{m}\Sigma_{i=1}^{m}(x^{(i)})^2 \\ x := x / \sigma$$

注意，上式中我们计算方差时没有减均值，这是因为第二步更新的时候均值已经被减掉了。

简单概括这个数学公式，就是“减均值，除方差”。

如果输入数据在各个分量上更加均匀，梯度下降的优化会更加便捷。

这里直接记住这个结论，不用过于在意它的数学原理。一种比较直观的解释是：如果分量大小不一，则参数w的每个分量的“作用”也会大小不一。如果w的每个分量都按差不多的“步伐”进行更新，那些“影响力更大”的w分量就会更新得过头，而“影响力更小”的w分量就更新得不足。这样，梯度下降法要耗费更多步才能找到最优值。

梯度爆炸/弥散

如果一个神经网络的层数过深，可能会出现梯度极大或极小的情况，让我们看看这是怎么回事。

假设我们有上图这样一个“很深”的神经网络。我们取消所有的激活函数（即$g(x)=x$），取消所有参数$b$（即$b=0$），那么这个网络的公式就是

$$\hat{Y}=A=W^W^NaN...W^1X$$

其中$W^NaN…W^1$都是2x2的矩阵。我们不妨假设它们都是同样的矩阵，那么上式可以写成

$$\hat{Y}=A=W^(W')^{L-1}X$$

如果$W’$长这个样子：

$$W'=\left[ \begin{matrix} &1.5 &0 \\ &0 &1.5 \\ \end{matrix} \right]$$

那么经过$L-1$次矩阵乘法后，这个矩阵就变成这个样子：

$$W'^{L-1}=\left[ \begin{matrix} &1.5^{L-1} &0 \\ &0 &1.5^{L-1} \\ \end{matrix} \right]$$

由于这里的数值是随着$L$成指数增长的，$L$稍微取一个大一点的值，最后算出来的$A$就会特别大。回顾一下前面的知识，最后一层的$dZ=A-Y$，而$dW$又是和$dZ$相关的。最后的$A$很大，会导致所有算出来的梯度都很大。

这里要批评一下这门课。课堂里有一个地方讲得不够清楚：为什么$A$很大，参数的梯度$dW$就很大。课堂里只是带了一句，说可以用类似的方法得出$dW$的增长规律和$A$类似。但这里漏了一条逻辑链：算梯度的时候，$A$和$dW$有关联性（$dZ$和$A$有关，$dW$和$dZ$有关）。直观上来看，$A$很大，不能推出梯度就很大。中间还是欠缺了一步逻辑推理的。学东西和看东西一定要养成批判性思维，考据每一步推理的合理性。

同理，如果矩阵里的数不是1.5，而是0.5，那么整个公式的数值就会指数级下降，从而导致梯度近乎“消失”。

梯度问题的解决方法——加权初始化

推荐一篇讲这个知识点的英文文章：https://towardsdatascience.com/weight-initialization-in-neural-networks-a-journey-from-the-basics-to-kaiming-954fb9b47c79.

刚刚我们讲到，梯度会爆炸或者弥散，本质原因是矩阵$W$的“大小”大于了1或者小于了1，从而使最后的计算结果过大或过小。但反过来想，如果我们令每一层的输出$A^{[l]}$的“大小”都在1附近，那么是不是就不会有梯度指数级变化的问题了呢？

让我们来看看该如何让每层输出$A^{[l]}$都保持一个合适的值。我们考察

$$Z=w_1x_1+w_2x_2...+w_nx_n$$

这个简单的网络。从直觉上看，如果$n$越大，则公式里的项越多，$Z$也越大。事实上，用统计学知识计算过后，能知道：若$w_i$都是满足标准正态分布的，则$Z$的方差是$n$。我们不希望$Z$的值太大或太小，希望能通过修改$w_i$的大小，让$Z$的方差尽可能等于1。

为了做到这一点，我们可以在$w$的初始化方法上做一点文章。我们可以改变$w$的方差，以改变$Z$的方差。其实，我们只要令$w$的方差为$\frac{1}{n}$就行了。用代码表示就是这样的:

W_l = np.random.randn(shape) * np.sqrt(1 / n[l-1])

别忘了哦，这里n[l-1]是第l层参数矩阵W_l的长度，即每个参数向量$w$的长度。

但由于每一层的输入不是$Z$，而是$A=g(Z)$，我们在算方差时还要考虑到激活函数$g$的影响。

经 Kaiming He 等人的研究，使用 Relu 时，初始化的权重用np.sqrt(2/ n[l-1])比较好，即用下面的代码：

W_l = np.random.randn(shape) * np.sqrt(2 / n[l-1])

对于 tanh 函数，令权重为 np.sqrt(1 / n[l-1])就行，这叫做 Xavier Initialization。还有研究表明用 np.sqrt(2 / (n[l-1]+n[l]))也行。

总结一下，为了缓解梯度爆炸或梯度弥散的问题，可以对参数使用加权初始化。只需要初始化时多乘一个小系数，这个问题就能很大程度上有所缓解。

梯度检查

进行深度学习编程时，梯度计算是比较容易出BUG的地方。我们可以用一种简单的方法来近似估计一个函数的导数，并将其与我们算出来的导数做一个对比，看看我们的导数计算函数有没有写错。

导数估计公式如下：

$$f'(\theta) \approx \frac{f(\theta+\epsilon)-f(\theta+\epsilon)}{2\epsilon}$$

这个式子随$\epsilon$收敛得较块，准确来说:

$$\begin{align} f(\theta+\epsilon)&\approx f(\theta)+\epsilon f'(\theta)+\frac{1}{2}\epsilon^2f''(\theta) + \frac{1}{6}\epsilon^3f'''(\theta)+... \\ \frac{f(\theta+\epsilon)-f(\theta)}{\epsilon} &\approx f'(\theta)+\frac{1}{2}\epsilon f''(\theta) \\ \frac{f(\theta+\epsilon)-f(\theta-\epsilon)}{2\epsilon} &\approx f'(\theta)+\frac{1}{6}\epsilon^2 f'''(\theta) \end{align}$$

当$lim_{\epsilon \to 0}$时，上面(2)式的收敛速度是$O(\epsilon)$，(3)式的收敛速度是$O(\epsilon^2)$。选用(3)式估计导数是一个更好的选择。

我们可以利用上面的公式调试深度学习中的梯度计算。其步骤如下：

1. 把所有参数$W^{[1]}, b^{[1]}…$ reshape 成向量，再把所有向量拼接(concatenate) 成一个新向量$\theta$。
2. 现在，我们有损失函数$J(\theta)$和导数$d\theta$。
3. 对于某一个参数$\theta_i$，计算其导数估计值：

$$\hat{d_{\theta_i}}=\frac{J(\theta_0, ..., \theta_i+\epsilon, ...)-J(\theta_0, ..., \theta_i-\epsilon, ...)}{2\epsilon}$$

1. 比较$\hat{d_{\theta_i}}, d_{\theta_i}$，计算误差值：

$$error=\frac{||\hat{d_{\theta_i}}-d_{\theta_i}||_2}{||\hat{d_{\theta_i}}||_2\cdot||d_{\theta_i}||_2}$$

1. 遍历所有$\theta_i$，做这个检查。

一般可以令$\epsilon=10^{-7}$。如果error在$10^{-7}$这个量级，则说明导数计算得没什么问题。$10^{-5}$可能要注意一下，而$10^{-3}$则大概率说明这里的导数算得有问题。

使用此梯度检查法时，有一些小提示：

• 不要每次训练的都用，只在训练前调试用。

梯度检查确实很慢，计算复杂度是$\Omega(|\theta|^2)$（这里没有用大O标记，因为复杂度的下界是那个值，而不是上界）（这个复杂度是$|\theta|$乘上算一遍推理的运算量得来的。推理至少遍历每个参数一遍，所以推理的复杂度是$\Omega(|\theta|)$）。

• 如果梯度检查出现了问题，尝试debug具体出错的参数。

• 别忘记损失函数中的正则化项。

• 无法调试 dropout.

• 有时候，当$W, b$过大时导数的计算才会出现较大的误差。可以尝试先训练几轮网络，等参数大了，再做一次梯度检查。

总结

这堂课的信息量十分大。让我们总结一下：

• 数据集划分
  • 训练集/开发集/测试集的意义
  • 怎么去根据数据规模划分不同的数据集
• 偏差与方差
  • 如何分辨高偏差与高方差问题
  • 高偏差与高方差问题的一般解决思路
• 正则化
  • 权重衰减
  • dropout
  • 数据增强
  • 提前停止
• 梯度问题
  • 梯度问题的产生原因
  • 缓解梯度问题的方法
• 梯度检查的实现

这堂课中，正则化和参数带权初始化是两个很重要的话题，展开来的话有很多东西要学。过段时间，我会在课堂内容的基础上，对这些知识进行拓展介绍。

代码实战

在本周的代码实战中，我们将继续以点集分类任务为例，完成参数初始化和正则化两项任务。

参数初始化

项目地址：https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/Initialization

在参数初始化问题中，我们要探究不同初始化方法对梯度更新的影响。假设我们有下面这样一个点集分类数据集：

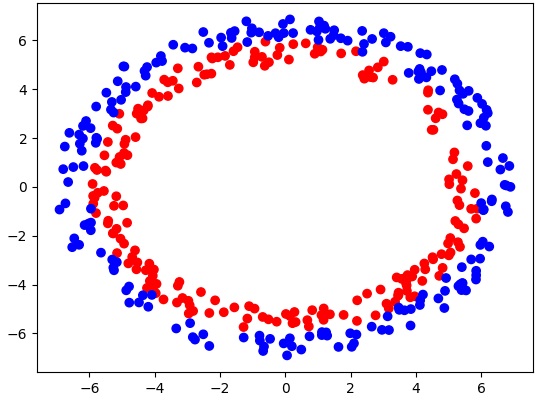
我们分别用下面三种方法去初始化参数：

if initialization == 'zeros':
    self.W.append(np.zeros((neuron_cnt[i + 1], neuron_cnt[i])))
elif initialization == 'random':
    self.W.append(
        np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) * 5)
elif initialization == 'he':
    self.W.append(
        np.random.randn(neuron_cnt[i + 1], neuron_cnt[i]) *
        np.sqrt(2 / neuron_cnt[i]))
self.b.append(np.zeros((neuron_cnt[i + 1], 1)))

如果使用0初始化的话，就会出现之前学过的“参数对称性”问题。这个网络几乎学不到任何东西：

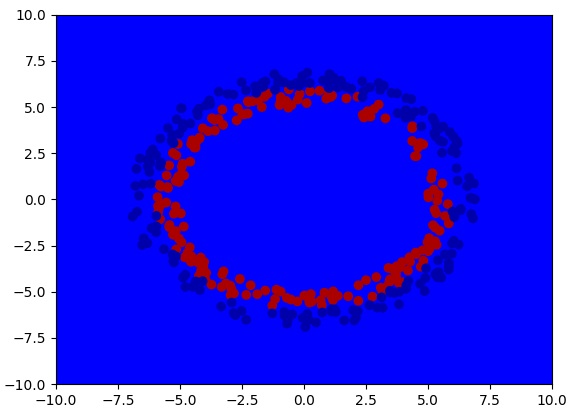
如果用比较大的值初始化的话，网络的梯度一直会很高，半天降不下来，学习速度极慢：

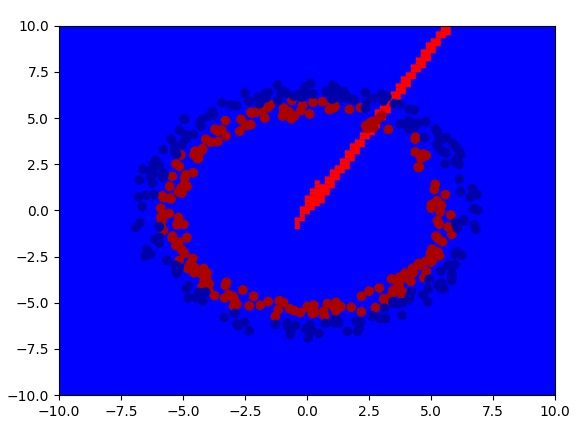
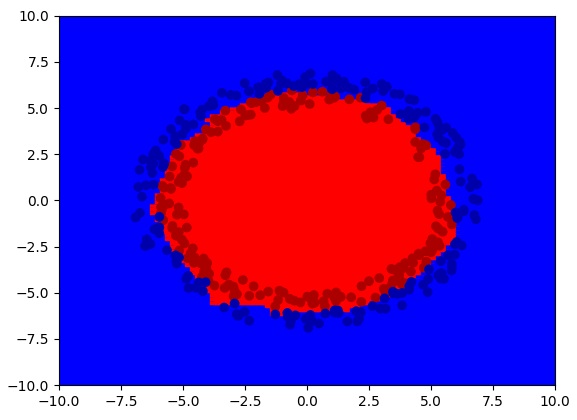
最后，我们使用比较高端的He Initialization.网络能够顺利学到东西了。

正则化

项目地址：https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/Regularization

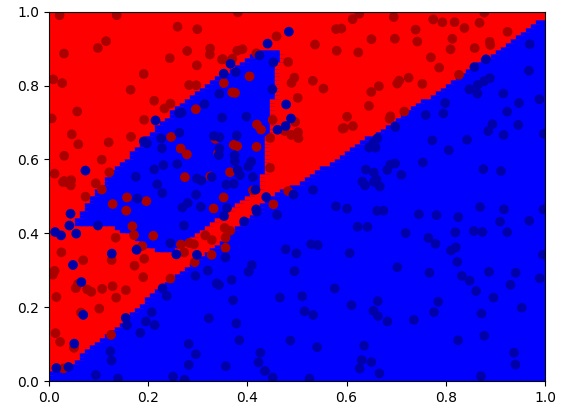
正则化要解决的是过拟合。为了“迫使”网络产生过拟合，我“精心”构造一个点集分类数据集：

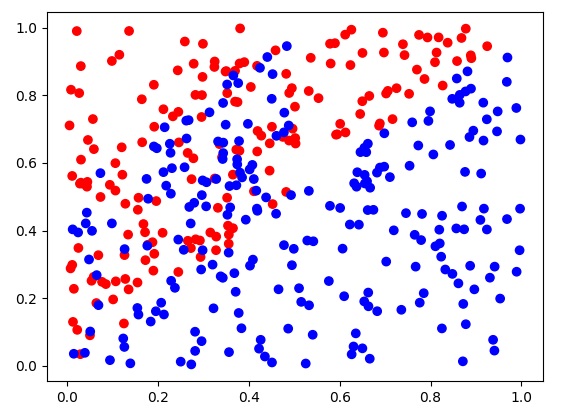
在这个分类任务中，比较理想的分类结果是一条直线。但是，由于表示噪声的蓝点比较多，网络可能会过拟合训练数据。

在这项实验中，我们将分别测试在“不使用正则化”、“使用正则项”、“使用dropout”这三种配置下网络的表现情况。

如我们所预计地，不使用正则化策略的网络会过拟合训练数据：

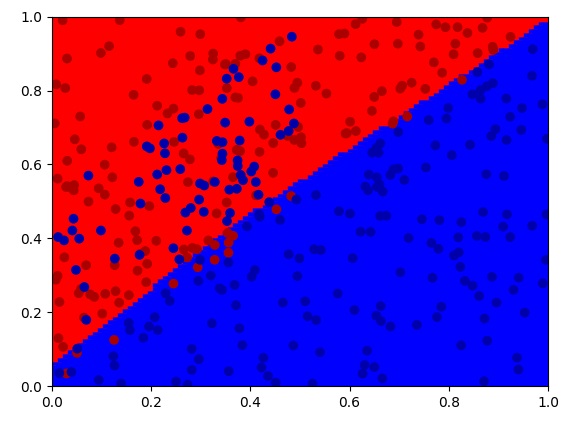
之后，我们按照公式，尝试给网络添加正则化项：

def gradient_descent(self, learning_rate):
    for i in range(self.num_layer):
        if self.weight_decay:
            LAMBDA = 4
            self.W[i] = (1 - learning_rate * LAMBDA / self.m
                          ) * self.W[i] - learning_rate * self.dW_cache[i]
            self.b[i] -= learning_rate * self.db_cache[i]
        else:
            self.W[i] -= learning_rate * self.dW_cache[i]
            self.b[i] -= learning_rate * self.db_cache[i]

def loss(self, Y: np.ndarray, Y_hat: np.ndarray) -> np.ndarray:
    if self.weight_decay:
        LAMBDA = 4
        tot = np.mean(-(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)))
        for i in range(self.num_layer):
            tot += np.sum(self.W[i] * self.W[i]) * LAMBDA / 2 / self.m
        return tot
    else:
        return np.mean(-(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)))

网络成功规避了过拟合。

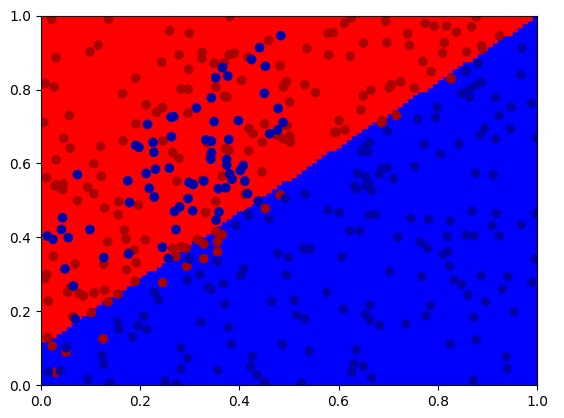
接下来，我们来尝试使用dropout策略。在训练时，我们每层有50%的概率丢掉训练结果：

def forward(self, X, train_mode=True):
    if train_mode:
        self.m = X.shape[1]
    A = X
    self.A_cache[0] = A
    for i in range(self.num_layer):
        Z = np.dot(self.W[i], A) + self.b[i]
        if i == self.num_layer - 1:
            A = sigmoid(Z)
        else:
            A = get_activation_func(self.activation_func[i])(Z)
        if train_mode and self.dropout and i < self.num_layer - 1:
            keep_prob = 0.5
            d = np.random.rand(*A.shape) < keep_prob
            A = A * d / keep_prob
        if train_mode:
            self.Z_cache[i] = Z
            self.A_cache[i + 1] = A

    return A

同样，使用dropout后，我们也得到了一个比较满意的分类结果：

欢迎大家自行调试这两个项目~