吴恩达《深度学习专项》笔记（七）：调参、批归一化、多分类任务、编程框架

学习提示

这周的知识点也十分分散，主要包含四项内容：调参、批归一化、多分类任务、编程框架。

通过在之前的编程项目里调整学习率，我们能够体会到超参数对模型效果的重要影响。实际上，选择超参数不是一个撞运气的过程。我们应该有一套系统的方法来快速找到合适的超参数。

两周前，我们学习了输入归一化。类似地，如果对网络的每一层都使用归一化，也能提升网络的整体表现。这样一种常用的归一化方法叫做批归一化。

之前，我们一直都在讨论二分类问题。而只要稍微修改一下网络结构和激活函数，我们就能把二分类问题的算法拓展到多分类问题上。

为了提升编程的效率，从这周开始，我们要学习深度学习编程框架。编程框架往往能够帮助我们完成求导的功能，我们可以把精力集中在编写模型的正向传播上。

课堂笔记

调参

调参的英文动词叫做tune，这个单词作动词时大部分情况下是指调音。这样一看，把调参叫做“调整参数”或“调试参数”都显得很“粗鲁”。理想情况下，调参应该是一个系统性的过程，就像你去给乐器调音一样。乱调可是行不通的。

超参数优先级

回顾一下，我们接触过的超参数有：

• 学习率 $\alpha$
• momentum $\beta$
• adam $\beta_1, \beta_2, \epsilon$
• 隐藏层神经元数
• 层数
• 学习率递减率
• mini-batch size

其中，优先级最高的是学习率。吴恩达老师建议大家调完学习率后，再去调$\beta$、隐藏层神经元数、mini-batch size。如果使用adam，则它的三个参数基本不用调。

超参数采样策略

在尝试各种超参数时，不要按“网格”选参数（如下图左半所示），最好随机选参数（如下图右半所示）：

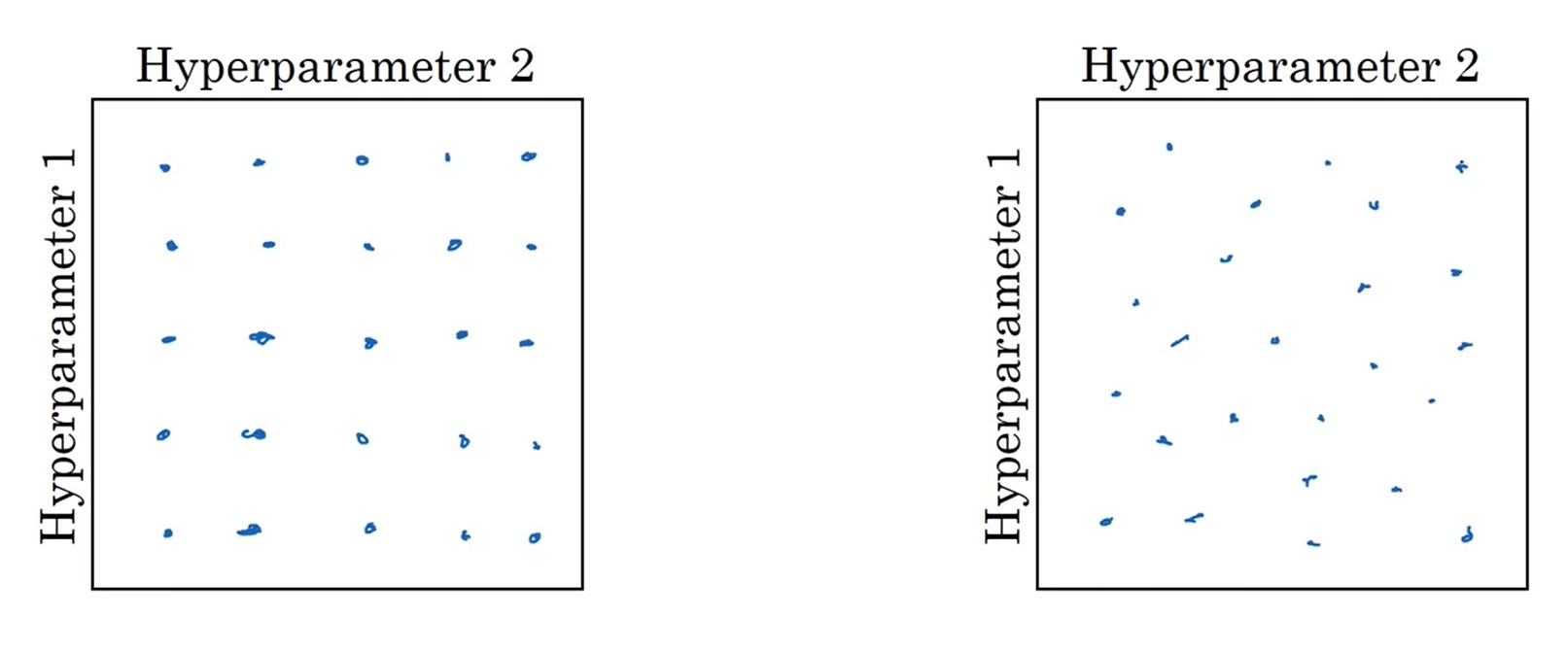
如果用网格采样法的话，你可能试了25组参数，每个参数只试了5个不同的值。而实际上，你试的两个参数中只有一个参数对结果的影响较大，另一个参数几乎不影响结果。最终，你尝试的25次中只有5次是有效的。

而采用随机采样法试参数的话，你能保证每个参数在每次尝试时都取不同值。这样试参数的效率会更高一点。

另外，调参时还有一个“由粗至精”的过程。如下图所示：

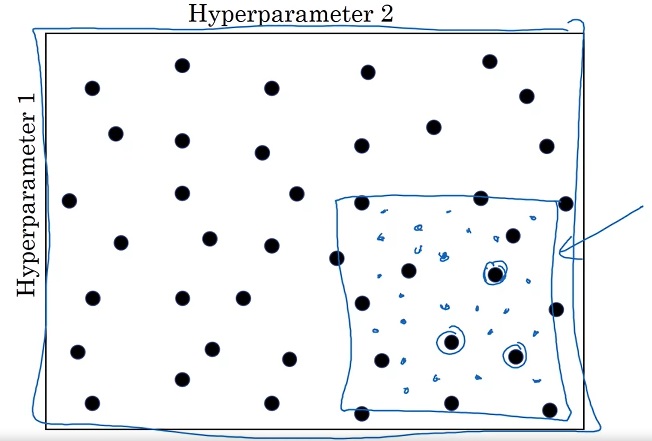
当我们发现某几个参数的结果比较优秀时，我们可以缩小搜索范围，仅在这几个参数附近进行搜索。

超参数搜索尺度

搜索参数时，要注意搜索的尺度。如果搜索的尺度不够恰当，我们大部分的调参尝试可能都是无用功。

比如当搜索学习率时，我们应该按0.0001, 0.001, 0.01, 0.1, 1这样指数增长的方式去搜索，而不应该按0.2, 0.4, 0.6, 0.8, 1这种均匀采样的方式搜索。这是因为学习率是以乘法形式参与计算，取0.4, 0.6, 0.8得到的结果可能差不多，按这种方式采样的话，大部分的尝试都是浪费的。而以0.001, 0.01, 0.1这种方式取学习率的话，每次的运行结果就会差距较大，每次尝试都是有意义的。

除了搜索学习率时用到的指数采样，还有其他的采样方式。让我们看调整momentum项$\beta$的情况。回忆一下，$\beta$取0.9，表示近10项的平均数；$\beta$取0.99，表示近100项的平均数。也就是说，$\beta$表示$\frac{1}{1-\beta}$项的平均数。我们可以对$\frac{1}{1-\beta}$进行指数均匀采样。

当然，有些参数是可以均匀采样的。比如隐藏层的个数，我们可以从[2, 3, 4]里面挑一个；比如每个隐藏层的神经元数，我们也可以直接均匀采样。

总结一下，我们在搜索超参数的时候，应该从超参数所产生的影响出发，考虑应该在哪个指标上均匀采样，再反推超参数的采样公式，而不一定要对超参数本身均匀采样。

当然了，如果我们不确定应该从哪个尺度对超参数采样，可以先默认使用均匀采样。因为我们会遵循由粗至精的搜索原则，尝试几轮后我们就能够观察出超参数的取值规律，从而在正确的尺度上对超参数进行搜索。

批归一化(Batch Normalization)

在第五篇笔记中，我们曾学习了输入归一化。其计算公式如下：

$$\begin{aligned} \mu&=\frac{1}{m}\Sigma_{i=1}^{m}x^{(i)} \\ x &:= (x - \mu) \\ \sigma^2&=\frac{1}{m}\Sigma_{i=1}^{m}(x^{(i)})^2 \\ x &:= x / \sigma \end{aligned}$$

通过归一化，神经网络第一层的输入更加规整，模型的训练速度能得到有效提升。

我们知道，神经网络的输入可以看成是第零层（输入层）的激活输出。一个很自然的想法是：我们能不能把神经网络每一个隐藏层的激活输出也进行归一化，让神经网络更深的隐藏层也能享受到归一化的加速？

批归一化(Batch Normalization)就是这样一种归一化神经网络每一个隐藏层输出的算法。准确来说，我们归一化的对象不是每一层的激活输出$a^{[l]}$，而是激活前的计算结果$z^{[l]}$。让我们看看对于某一层的激活前输出$z=z^{[l]}$，我们该怎么进行批归一化。

首先，还是先获取符合标准正态分布的归一化结果$z^{(i)}_{norm}$：

$$\begin{aligned} & Input \ z^{(1)}, z^{(2)}, ...z^{(m)} \\ & \mu=\frac{1}{m}\Sigma_i^{m}z^{(i)} \\ & \sigma^2=\frac{1}{m}\Sigma_i^{m}(z^{(i)}- \mu)^2\\ & z^{(i)}_{norm}=\frac{z^{(i)}-\mu}{\sigma} \end{aligned}$$

我们不希望每一层的输出都固定为标准正态分布，而是希望网络能够自己选择最恰当的分布。因此，我们可以用下式计算最终的批归一化结果：

$$\tilde{z}^{(i)}=\gamma z^{(i)}_{norm} + \beta$$

其中$\tilde{z}^{(i)}$是最终的批归一化结果，$\gamma, \beta$都是可学习参数，分别影响新分布的方差与均值。

为什么我们不希望数据的分布总是标准正态分布呢？可以考察一个即将送入sigmoid的$z$。sigmoid在[-1, 1]这段区间内近乎是一个线性函数，为了利用该激活函数的非线性区域，我们应该让$z$的取值范围更大一点，即让$z$的方差大于1。

这里的$\beta$和梯度下降算法里的$\beta$不是同一回事，只是这几个算法的原论文里都使用了$\beta$这个符号。

使用批归一化后，原来的神经网络计算公式需要做出一些调整。之前，$z^{(i)}$的计算公式如下：

$$z^{(i)}=Wa^{(i)}+b$$

现在，我们会把$z^{(i)}$的均值归一化到0。因此，$+b$成为了一个冗余的操作。使用了批归一化后，$z^{(i)}$应该按下面的方法计算：

$$z^{(i)}=Wa^{(i)}$$

总结一下，加入批归一化后，神经网络的计算过程如下所示：

$$X \to Z^{[1]}(use \ W^{[1]}) \to \tilde{Z}^{[1]}(use \ \beta^{[1]}, \gamma^{[1]}) \to A^{[1]} \to ...$$

注意，使用向量化计算后，$\tilde{Z}^{[l]}$的计算公式应该如下：

$$\tilde{Z}^{[l]}=\gamma^{[l]} \ast Z_{norm}^{[l]} + \beta^{[l]}$$

其中$\gamma^{[l]}$和$\beta^{[l]}$的形状都是$(n^{[l]}, 1)$

课堂里没有介绍批归一化的求导公式。这里补充一下：

$$\begin{aligned} d\beta &= \frac{1}{m}dA \\ d\gamma &= \frac{1}{m}dA \ast Z_{norm}^{[l]} \end{aligned}$$

使用批归一化后，常见优化算法（mini-batch, momentum, adam, …）仍能照常使用。

直观理解批归一化的作用

对于神经网络中较深的层，它们只能“看到”来自上一层的激活输出，而不知道较浅的层的存在。如下图所示，对于第3层，它只知道第2层的激活输出$A^{[2]}$。

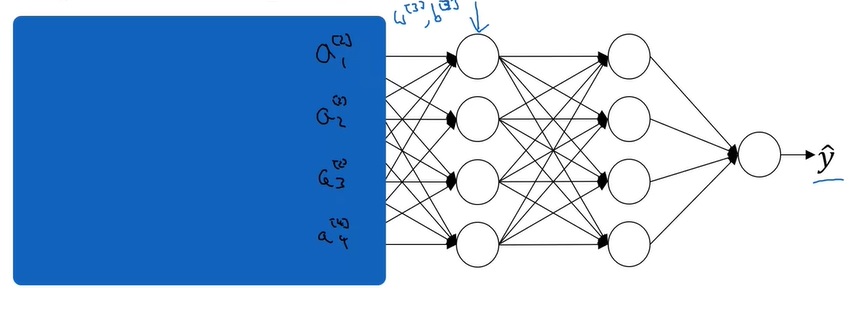
这样，经过一段时间的训练后，网络的第3层和第4层知道了如何较好地把$A^{[2]}$映射成$\hat{y}$。

可是，$A^{[2]}$并不是神经网络的真实输入。神经网络真正的结构如下：

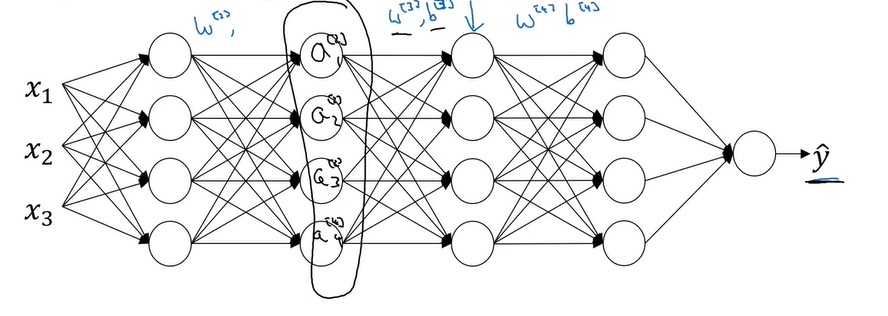
$A^{[2]}$其实还受到神经网络前2层参数的影响。一旦前2层的参数更新，$A^{[2]}$的分布也会随之改变，第3层和第4层可能要从头学习$A^{[2]}$到$\hat{y}$的映射关系。

与之相比，使用了批归一化后，神经网络每一层的输出都会落在一个类似的分布里。这样，浅层和深层之间就没有那么强的依赖关系，较深的层能够更快完成学习。

顺带一提，当我们用批归一化的同时，如果还使用了mini-batch，则批归一化还能稍微起到一点正则化的作用。这是因为在mini-batch上每层批归一化用到的方差和均值是不准确的，这种“带噪音”的批归一化能够起到和dropout类似的作用，防止神经网络以较大的权重依赖于少数神经元。

测试时的批归一化

我们刚刚学习的批归一化操作，其实都是针对训练而言的。在训练时，我们有大批的数据，可以轻松算出每一层中间结果$Z^{[l]}$的均值和方差。但是，在测试时，我们可能只会对一项输入进行计算。对一项输入计算均值和方差是没有意义的。因此，我们要想办法决定测试时$Z^{[l]}\to Z_{norm}^{[l]}$用到的均值和方差。

我们可以用每一个mini-batch的均值和方差的指数加权移动平均数作为测试时的均值和方差。

Softmax 与多分类问题

之前我们一直都在讨论二分类问题。比如，辨别一张图片是不是小猫。当我们把二分类问题拓展到多分类问题时，问题的数学模型会发生哪些变化呢？

首先，我们来看一下多分类问题的定义。在多分类问题中，我们要要判断一个输入是属于$C$种类型中的哪一种。比如我们希望判断一张图片里的生物是属于小猫、小狗、小鸡、其他这$C=4$类中的哪一种。

在二分类问题中，我们用1表示“是某一类”，0表示“不是某一类”。我们只需要计算$P(\hat{y}=1|x)$这一个概率。而多分类问题中，我们用一个数字表示一种类别，比如0表示“其他”，1表示“小猫”，2表示“小狗”，3表示“小鸡”。这样，我们就应该计算多个概率，比如$P(\hat{y}=0|x), P(\hat{y}=1|x), P(\hat{y}=2|x), P(\hat{y}=3|x)$这四个概率。

多分类问题的示意图和一个可能的多分类神经网络如下图所示（注意，该网络有4个输出）：

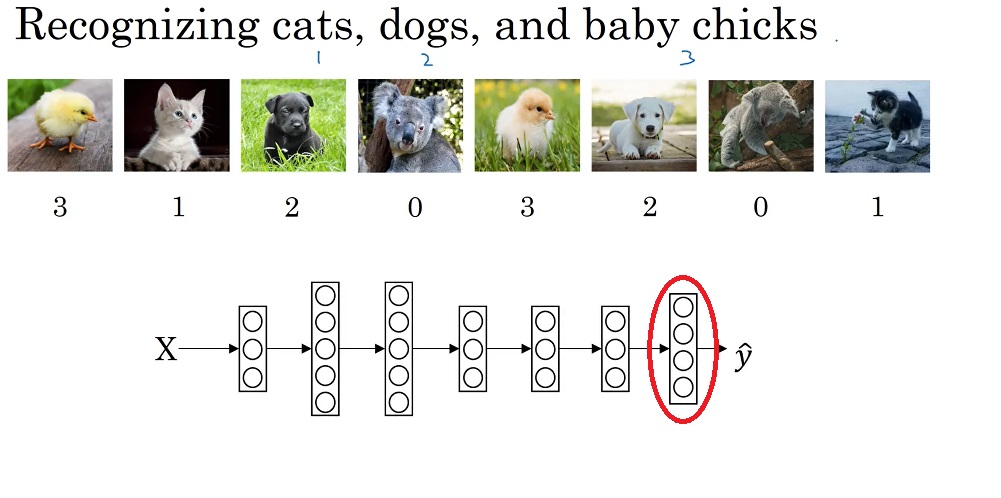
接着，我们来看看多分类问题带来了哪些新的困难。在二分类问题中，我们得到了最后一层的计算结果$z^{[L]}$，我们要用sigmoid把它映射到表示概率的[0, 1]上。而多分类问题中，同理，我们要把神经网络最后一层的计算结果$z^{[L]}$映射成一些有实际意义的概率值。具体而言，我们应让所有分类概率之和为1，即$\Sigma_{i=1}^CP(\hat{y}=i|x)=1$。为了达到这个目的，我们要引入一个激活函数——softmax。

和其他定义在一个实数上的激活函数不同，softmax定义在一个向量上，其计算方式为：

$$\begin{aligned} &Input \ z^{[L]} \\ &output \ a^{[L]} \\ &t = e^{z^{[L]}} \\ &a^{[L]} = \frac{t}{\Sigma_{i=1}^Ct_i} \end{aligned}$$

注意，上式中所有运算都是逐元素运算。比如在上面提到的有四个类别的分类问题中，$z^{[L]}$是一个形状为$(4, 1)$的张量，经过逐元素运算后，$t, a^{[L]}$都是形状为$(4, 1)$的张量。

上述描述可能比较抽象，让我们看课件里的一个具体例子：

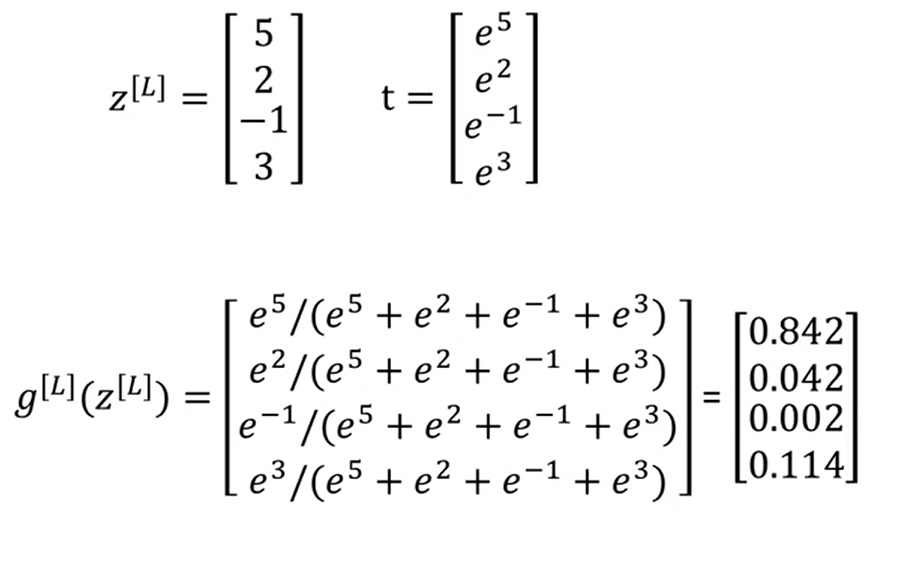
假设$z^{[L]}=[5, 2, -1, 3]$，则$t=[e^5, e^2, e^{-1}, e^3], \Sigma_{j=1}^4t_j\approx176.3,a^{[L]}_1\approx0.842,a^{[L]}_2\approx0.042,a^{[L]}_3\approx0.002,a^{[L]}_4\approx0.114$。

softmax的计算方法可以总结为：求指数，归一化。本质上来说，softmax就是把向量每个分量的自然指数作为一个新的标准，在这个标准上进行标准归一化操作。

为什么要使用向量每个分量的自然指数作为归一化的变量，而不直接对原向量做标准归一化呢？可以考虑[1, 2], [10, 20]这两个向量。如果直接对这两个量进行进行归一化，算出来的概率都是[0.33, 0.67]。而实际上，第一个向量可能对应一幅比较模糊的输入，第二个向量可能对应一幅比较清楚的输入。显然，在更清晰的输入上，我们更有把握说我们的分类结果是正确的。通过使用softmax，我们可以放大数值的影响，[10, 20]相比[1, 2]，我们更有把握说输入是属于第二个类别的。该解释参考自https://stackoverflow.com/questions/17187507/why-use-softmax-as-opposed-to-standard-normalization

在C=2时，softmax会退化成sigmoid。也就是说，softmax是sigmoid在多分类任务上的推广。

softmax这个名字，其实衍生自hardmax这个词。使用hardmax时，输入会被映射成[1, 0, 0, 0]这样一个one-hot向量。这种最大值太严格（hard）了，所以有相对来说比较宽松（soft）的最大值计算方法softmax。

使用了softmax后，还需要调整的是网络的loss。推广到多分类后，我们要使用的loss是

$$L(y, \hat{y}) = -\Sigma_{i=1}^Cy_ilog\hat{y_i}$$

，其中$y_i$不是一个表示类别的整数，而是一个one-hot编码的向量。比如在一共有4类时，标签2的one-hot编码是：

$$\left[ \begin{aligned} 0 \\ 0 \\ 1 \\ 0 \end{aligned} \right]$$

假设整个标签数据集为$[0, 1, 3, 2]$，则参与网络运算时用到的$Y$应该是：

$$\left[ \begin{aligned} 1 \ 0 \ 0 \ 0\\ 0 \ 1 \ 0 \ 0\\ 0 \ 0 \ 0 \ 1\\ 0 \ 0 \ 1 \ 0 \end{aligned} \right]$$

在编程时，数据集一般只会提供用整数表示的标签。为了正确使用loss，我们需要多加一步转换到one-hot编码的步骤。

和逻辑回归类似，计算梯度时，$dZ^{[L]}=\hat{Y}-Y$这个等式依然成立，我们可以用它跳一个算梯度的步骤。

编程框架

由于深度学习的开发者越来越多，许多开源深度学习编程框架相继推出，比如：

• Caffe/Caffe2
• Torch
• TensorFlow
• Keras
• mxnet
• PaddlePaddle
• CNTK
• DL4J
• Lasagne
• Theano

这些编程框架不仅封装了常见的深度学习数学函数，如sigmoid、softmax、卷积，还支持自动求导的功能——这是深度学习编程框架最吸引人的一点。在使用编程框架时，我们只需要编写前向传播的过程，框架就会自动执行梯度计算，以辅助我们完成反向传播。

目前，学术界最常用的是Torch的Python版PyTorch。第二常用的是TensorFlow。

在选择编程框架时，我们要考虑以下几点：

• 易用性（能否快速开发与部署）
• 运行性能
• 是否真正开源

前两点注意事项毋庸置疑。框架之于编程语言，就像高级语言之于汇编语言一样。我们选择编程框架而不去从零编程，最主要的原因就是开发效率。使用框架能够节约大量的开发时间，有助于项目的迭代。而使用统一的框架，往往会损失一些效率，这些损失的效率不能太多。

第三点要着重强调一下。很多框架打着开源的名号，实际上却是某个公司在维护。如果这个公司哪天不想维护了，放弃继续开源，那么你的开发就会受到很大的影响。

这周的课还介绍了TensorFlow的用法，我会在编程实战中补充这方面的知识。

总结

这堂课的知识点有：

• 调参
  • 优先级
  • 采样策略
  • 搜索尺度
• 批归一化
  • 在网络中的位置
  • 作用（归一化、新分布）
  • 超参数与公式
  • 测试时的处理方式
• 多分类问题
  • softmax
  • loss
• 编程框架
  • 了解常见的编程框架
  • 选择编程框架的角度

通过这三周的学习，我们掌握了深度学习各方面的知识，能够用多种方式提升我们深度学习项目的性能了。

这周的编程要用到TensorFlow。我将另开一篇文章介绍本周的代码实战项目。