吴恩达《深度学习专项》笔记（十一）：深度卷积模型——从示例中学习

学习提示

上周，我们学完了CNN的基础组成模块。而从这周开始，我们要换一种学习方式：我们会认识一些经典的CNN架构，从示例中学习。一方面来说，通过了解他人的网络，阅读他人的代码，我们能够更快地掌握如何整合CNN的基础模块；另一方面，CNN架构往往泛化能力较强，学会了其他任务中成熟的架构，可以把这些架构直接用到我们自己的任务中。

接下来，我们会按照CNN的发展历史，认识许多CNN架构。首先是经典网络：

• LeNet-5
• AlexNet
• VGG

之后是近年来的一些网络：

• ResNet
• Inception
• MobileNet

我们不会把这些研究的论文详细过一遍，而只会学习各研究中最精华的部分。学有余力的话，最好能在课后把论文自己过一遍。

课堂笔记

经典网络

LeNet-5

LeNet-5是用于手写数字识别（识别0~9的阿拉伯数字）的网络。它的结构如下：

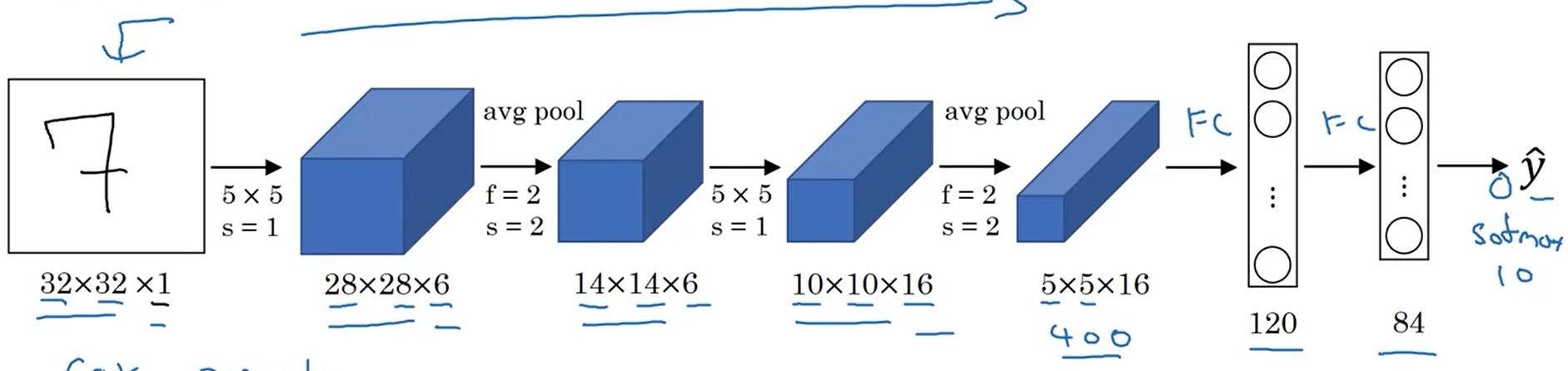
网络是输入是一张[32, 32, 1]的灰度图像，输入经过4个卷积+池化层，再经过两个全连接层，输出一个0~9的数字。这个网络和我们上周见过的网络十分相似，数据体的宽和高在不断变小，而通道数在不断变多。

这篇工作是1998年发表的，当时的神经网络架构和现在我们学的有不少区别：

• 当时padding还没有得到广泛使用，数据体的分辨率会越降越小。
• 当时主要使用平均池化，而现在最大池化更常见。
• 网络只输出一个值，表示识别出来的数字。而现在的多分类任务一般会输出10个值并使用softmax激活函数。
• 当时激活函数只用sigmoid和tanh，没有人用ReLU。
• 当时的算力没有现在这么强，原工作在计算每个通道卷积时使用了很多复杂的小技巧。而现在我们直接算就行了。

LeNet-5只有6万个参数。随着算力的增长，后来的网络越来越大了。

AlexNet

AlexNet是2012年发表的有关图像分类的CNN结构。它的输入是[227, 227, 3]的图像，输出是一个1000类的分类结果。

原论文里写的是输入形状是[224, 224, 3]，但实际上这个分辨率是有问题的，按照这个分辨率是算不出后续结果的分辨率的。但现在一些框架对AlexNet的复现中，还是会令输入的分辨率是224。这是因为框架在第一层卷积中加了一个padding的操作，强行让后续数据的分辨率和原论文对上了。

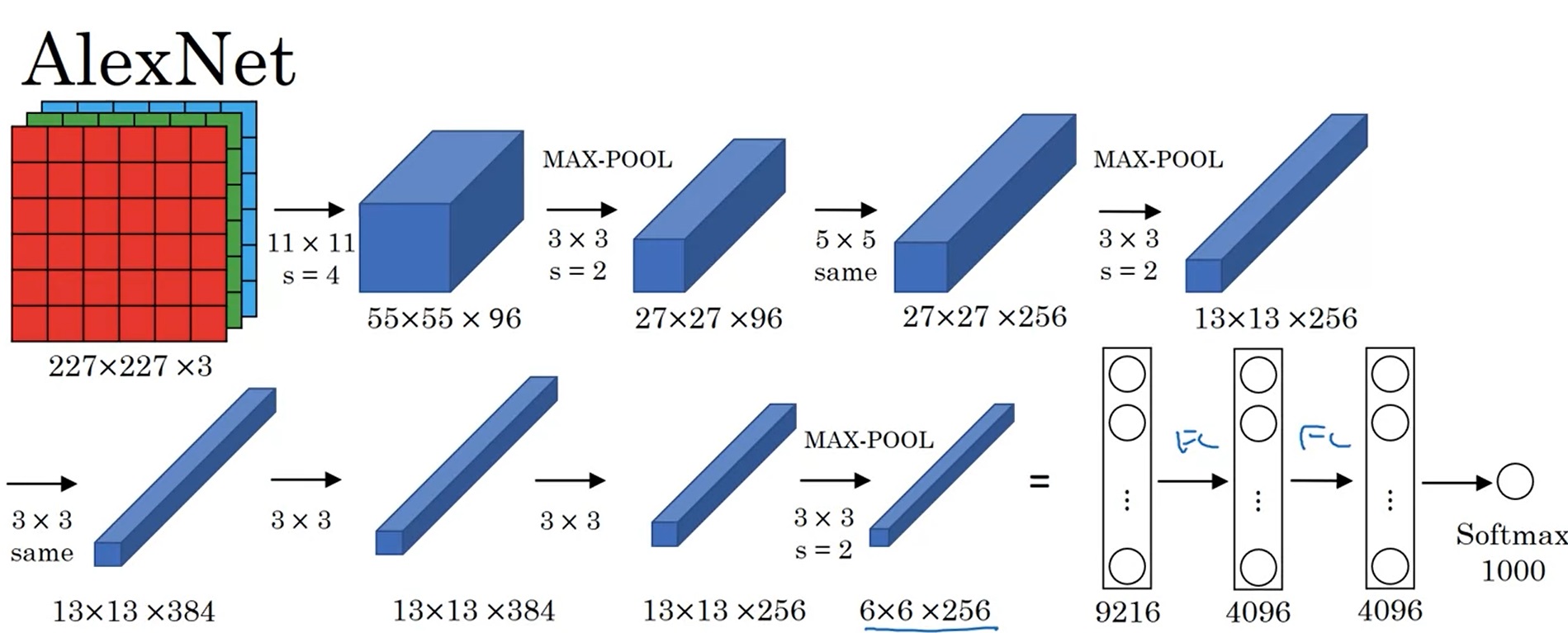
AlexNet和LeNet-5在架构上十分接近。但是，AlexNet做出了以下改进：

• AlexNet用了更多的参数，一共有约6000万个参数。
• 使用ReLU作为激活函数。

AlexNet还提出了其他一些创新，但与我们要学的知识没有那么多关系：

• 当时算力还是比较紧张，AlexNet用了双GPU训练。论文里写了很多相关的工程细节。
• 使用了Local Response Normalization这种归一化层。现在几乎没人用这种归一化。

AlexNet中的一些技术在今天看来，已经是常识般的存在。而在那个年代，尽管深度学习在语音识别等任务上已经初露锋芒，人们还没有开始重视深度学习这项技术。正是由于AlexNet这一篇工作的出现，计算机视觉的研究者开始关注起了深度学习。甚至在后来，这篇工作的影响力已经远超出了计算机视觉社区。

VGG-16

VGG-16也是一个图像分类网络。VGG的出发点是：为了简化网络结构，只用3x3等长(same)卷积和2x2最大池化。

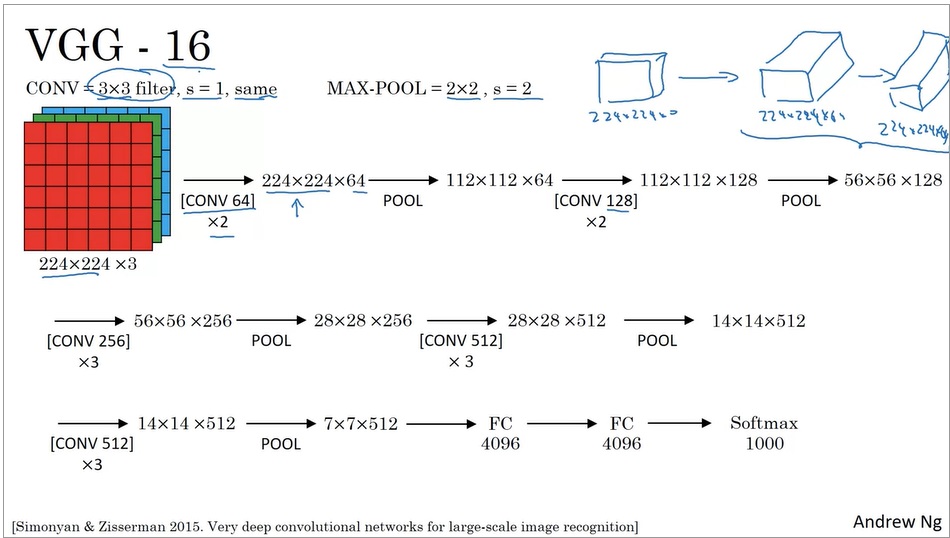
可以看出，VGG也是经过了一系列的卷积和池化层，最后使用全连接层和softmax输出结果。顺带一提，VGG-16里的16表示有16个带参数的层。

VGG非常庞大，有138M(1.38亿)个参数。但是它简洁的结构吸引了很多人的关注。

吴恩达老师鼓励大家去读一读这三篇论文。可以先看AlexNet，再看VGG。LeNet有点难读，可以放到最后去读。

ResNets（基于残差的网络）

非常非常深的神经网络是很难训练的，这主要是由梯度爆炸/弥散问题导致的。在这一节中，我们要学一种叫做“跳连(skip connection)”的网络模块连接方式。使用跳连，我们能让浅层模块的输出直接对接到深层模块的输入上，进而搭建基于残差的网络，解决梯度爆炸/弥散问题，训练深达100层的网络。

残差块

回忆一下，在全连接网络中，假如我们有中间层的输出$a^{[l]}, a^{[l+2]}$，$a^{[l+2]}$是怎么由$a^{[l]}$算出来的呢？我们之前用的公式如下：

$$\begin{aligned} z^{[l+1]}&=W^{[l+1]}a^{[l]}+b^{[l+1]} \\ a^{[l+1]}&=g(z^{[l+1]}) \\ z^{[l+2]}&=W^{[l+2]}a^{[l+1]}+b^{[l+2]} \\ a^{[l+2]}&=g(z^{[l+2]}) \\ \end{aligned}$$

也就是说，$a^{[l]}$要经过一个线性层、一个激活函数、一个线性层、一个激活函数，才能传递到$a^{[l+2]}$，这条路径非常长：

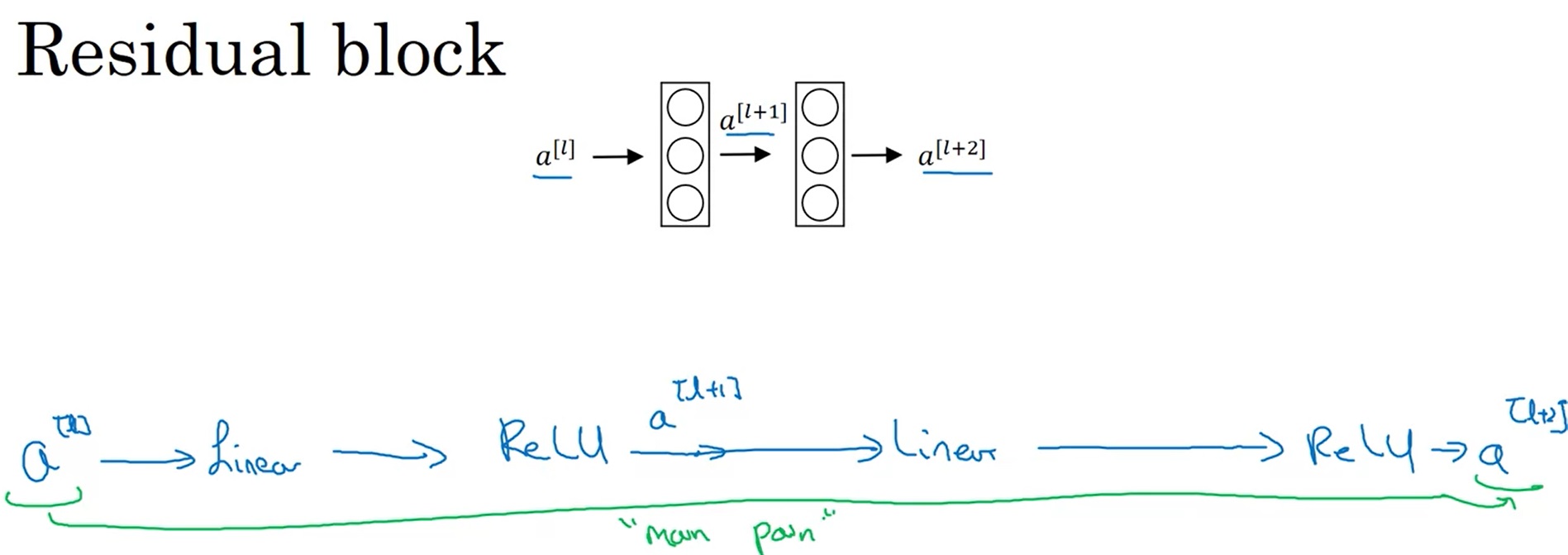
而在残差块(Residual block)中，我们使用了一种新的连接方法：

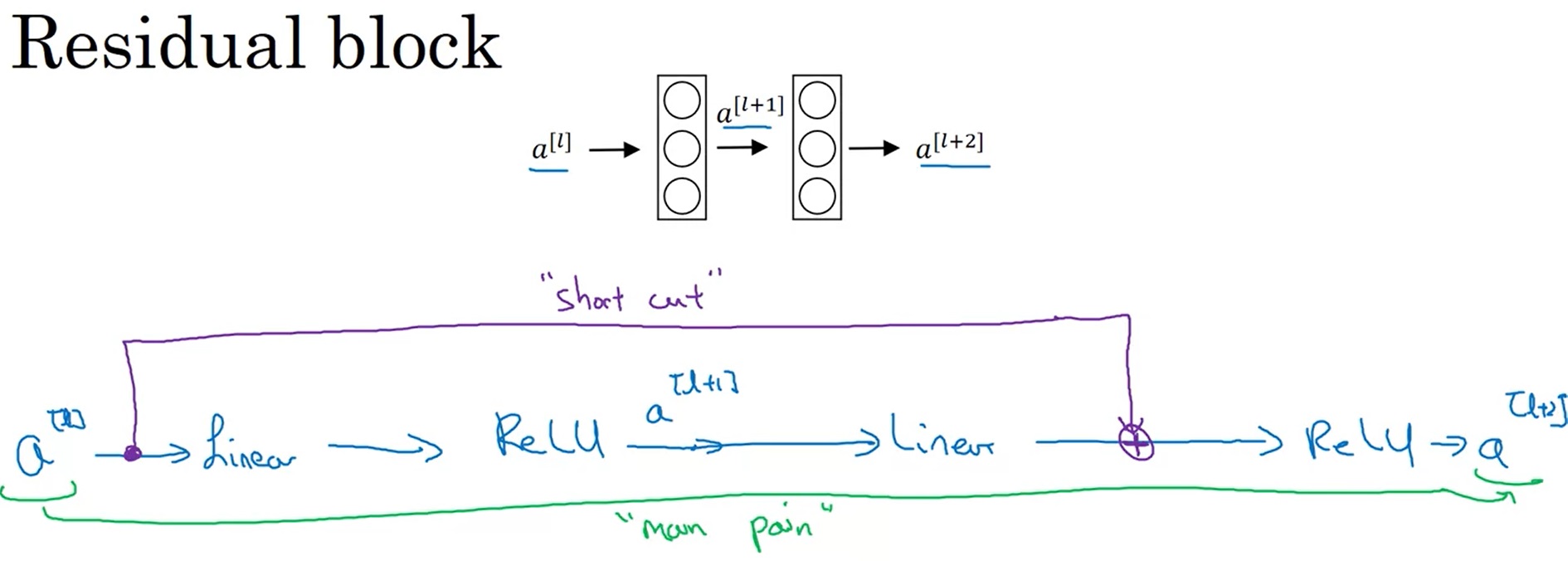
$a^{[l]}$的值被直接加到了第二个ReLU层之前的线性输出上，这是一种类似电路中短路的连接方法（又称跳连）。这样，浅层的信息能更好地传到深层了。

使用这种方法后，计算公式变更为：

$$\begin{aligned} z^{[l+1]}&=W^{[l+1]}a^{[l]}+b^{[l+1]} \\ a^{[l+1]}&=g(z^{[l+1]}) \\ z^{[l+2]}&=W^{[l+2]}a^{[l+1]}+b^{[l+2]} \\ a^{[l+2]}&=g(z^{[l+2]}+a^{[l]}) \\ \end{aligned}$$

残差块中还有一个要注意的细节。$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$这个式子能够成立，实际上是默认了$a^{[l+2]}, a^{[l]}$的维度相同。而一旦$a^{[l+2]}$的维度发生了变化，就需要用下面这种方式来调整了。

$a^{[l+2]}=g(z^{[l+2]}+W’a^{[l]})$

我们可以用一个$W’$来完成维度的转换。为了方便理解，我们先让所有$a$都是一维向量，$W’$是矩阵。这样，假设$a^{[l+2]}$的长度是256，$a^{[l]}$的长度是128，则$W’$的形状就是$256 \times 128$。

但实际上，$a$是一个三维的图像张量，三个维度的长度都可能发生变化。因此，对于图像，上式中的$W’$应该表示的是一个卷积操作。通过卷积操作，我们能够减小图像的宽高，调整图像的通道数，使得$a^{[l]}$和$a^{[l+2]}$的维度完全相同。

残差网络

在构建残差网络ResNet时，只要把这种残差块一个一个拼接起来即可。或者从另一个角度来看，对于一个“平坦网络”（”plain network”, ResNet论文中用的词，用于表示非残差网络），我们只要把线性层两两打包，添加跳连即可。

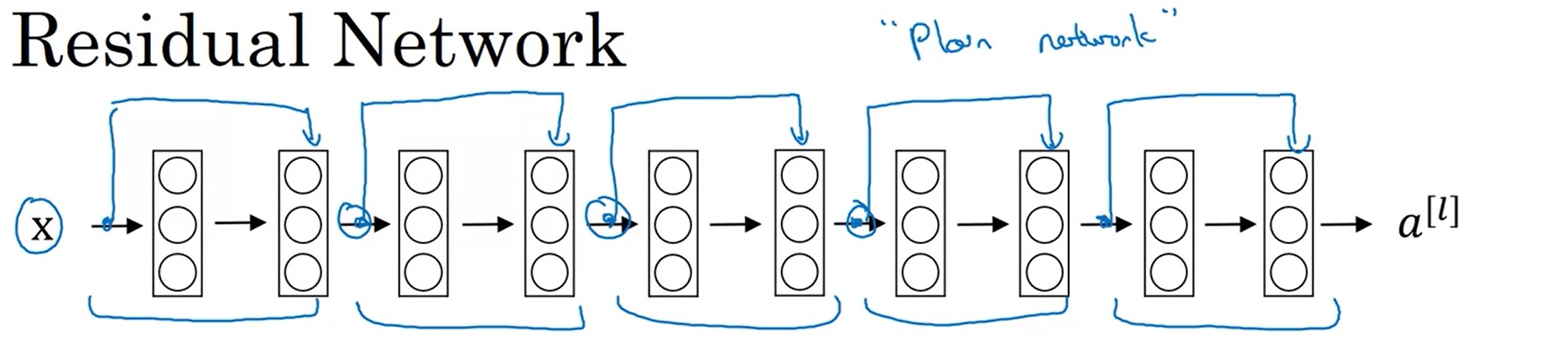
残差块起到了什么作用呢？让我们看看在网络层数变多时，平坦网络和残差网络训练误差的变化趋势：

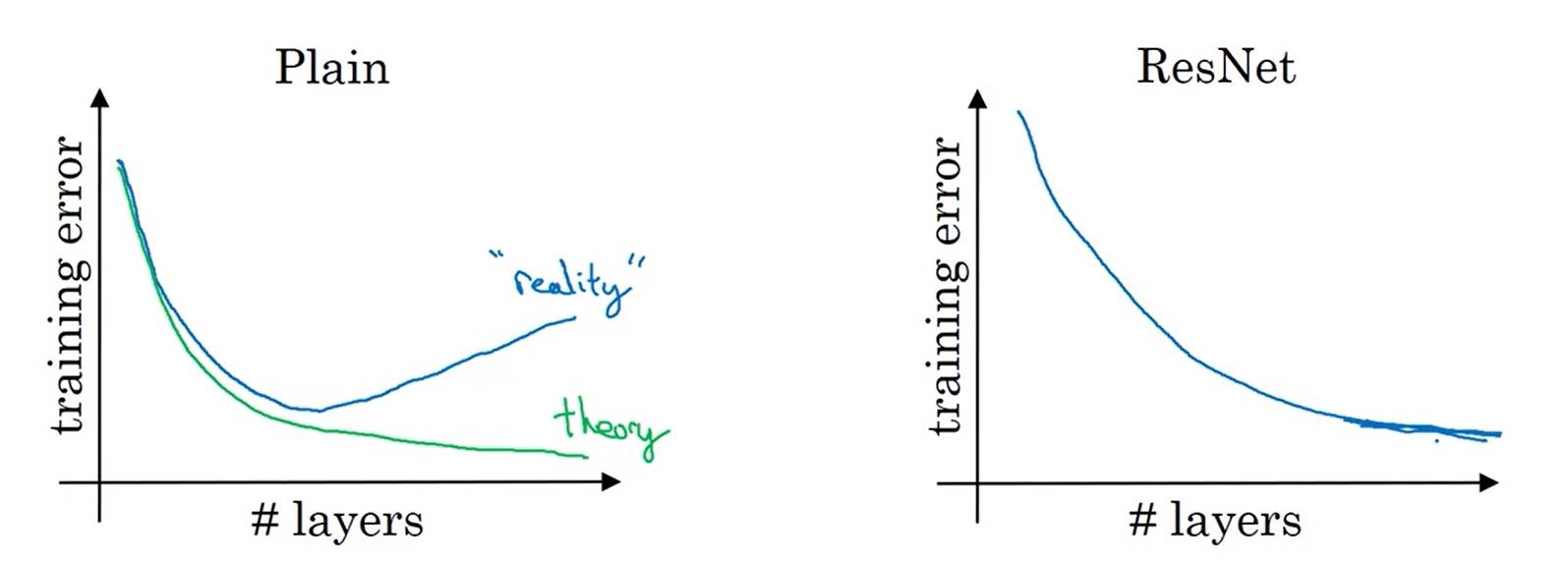
理论上来说，层数越深，训练误差应该越低。但在实际中，对平坦网络增加深度，反而会让误差变高。而使用ResNet后，随着深度增加，训练误差起码不会降低了。

正是有这样的特性，我们可以用ResNet架构去训练非常深的网络。

为什么ResNet是有这样的特性呢？我们还是从刚刚那个ResNet的公式里找答案。

假设我们设计好了一个网络，又给它新加了一个残差块，即多加了两个卷积层，那么最后的输出可以写成：

$$a^{[l+2]}=g(z^{[l+2]}+a^{[l]}),$$

即

$$\begin{aligned} a^{[l+2]}&=g(z^{[l+2]}+a^{[l]}) \\ a^{[l+2]}&=g(W^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]}) \\ \end{aligned}$$

由于正则化的存在，所有$W$和$b$都倾向于变得更小。极端情况下，$W, b$都变为0了。那么，

$$\begin{aligned} a^{[l+2]}&=g(W^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]}), \\ a^{[l+2]}&=g(a^{[l]}). \\ \end{aligned}$$

再不妨设$g=ReLU$。则因为$a^{[l]}$也是ReLU的输出，有

$$\begin{aligned} a^{[l+2]}&=g(a^{[l]}), \\ a^{[l+2]}&=a^{[l]}. \\ \end{aligned}$$

这其实是一个恒等映射，也就是说，新加的残差块对之前的输出没有任何影响。网络非常容易学习到恒等映射。这样，最起码能够保证较深的网络不比浅的网络差。

准备好了所有基础知识，我们来看看完整的ResNet长什么样。

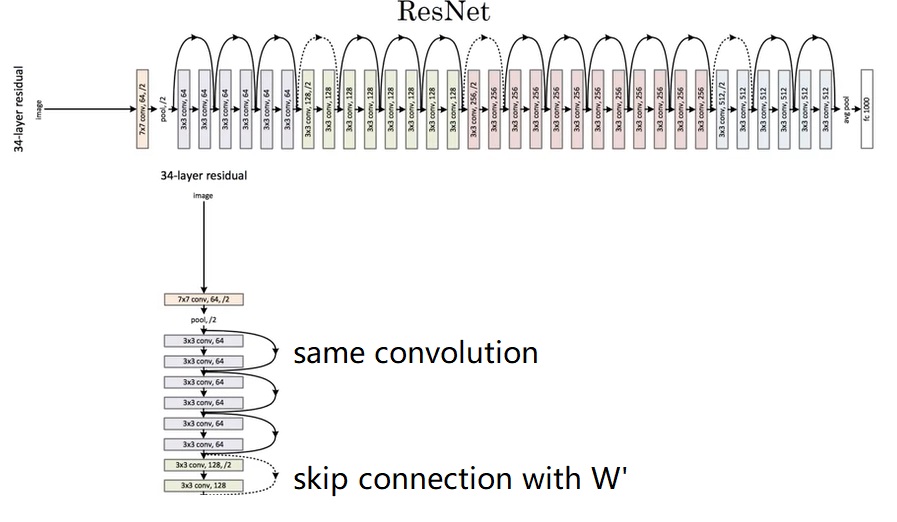
ResNet有几个参数量不同的版本。这里展示的叫做ResNet-34。完整的网络很长，我们只用关注其中一小部分就行了。

一开始，网络还是用一个大卷积核大步幅的卷积以及一个池化操作快速降低图像的宽度，再把数据传入残差块中。和我们刚刚学的一样，残差块有两种，一种是维度相同可以直接相加的（实线），一种是要调整维度的（虚线）。整个网络就是由这若干个这样的残差块组构成。经过所有残差块后，还是和经典的网络一样，用全连接层输出结果。

这里，我们只学习了残差连接的基本原理。ResNet的论文里还有更多有关网络结构、实验的细节。最好能读一读论文。当然，这周的编程实战里我们也会复现ResNet，以加深对其的理解。

Inception 网络

我们已经见过不少CNN的示例了。当我们仿照它们设计自己的网络时，或许会感到迷茫：有3x3, 5x5卷积，有池化，该怎么选择每一个模块呢？Inception网络给了一个解决此问题的答案：我全都要。

Inception网络用到了一种特殊的1x1卷积。我们会先学习1x1卷积，再学习Inception网络的知识。

1x1卷积

用1x1的卷积核去卷一幅图像，似乎是一件很滑稽的事情。假设一幅图像的数字是[1, 2, 3]，卷积核是[2]，那么卷出来的图像就是[2, 4, 6]。这不就是把每个数都做了一次乘法吗？

对于通道数为1的图像，1x1卷积确实没什么大用。而当通道数多起来后，1x1卷积的意义就逐渐显现出来了。思考一下，对多通道的图像做1x1卷积，就是把某像素所有通道的数字各乘一个数，求和，加一个bias，再通过激活函数。这是计算一个输出结果的过程，而如果有多个卷积核，就可以计算出多个结果。（下图中，蓝色的数据体是输入图像，黄色的数据体是1x1的卷积核。两个数据体重合部分的数据会先做乘法，再求和，加bias，经过激活函数。）

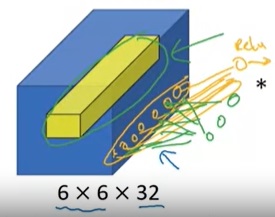
这个过程让你想起了什么？没错，正是最早学习的全连接网络。1x1卷积，实际上就是在各通道上做了一次全连接的计算。1x1卷积的输入通道数，就是全连接层上一层神经元的数量；1x1卷积核的数量，就是这一层神经元的数量。

1x1卷积主要用于变换图像的通道数。比如要把一个192通道数的图像变成32通道的，就应该用32个1x1卷积去卷原图像。

Inception块的原理

在Inception网络中，我们会使用这样一种混合模块：对原数据做1x1, 3x3, 5x5卷积以及最大池化，得到通道数不同的数据体。这些数据体会被拼接起来，作为整个模块的输出。

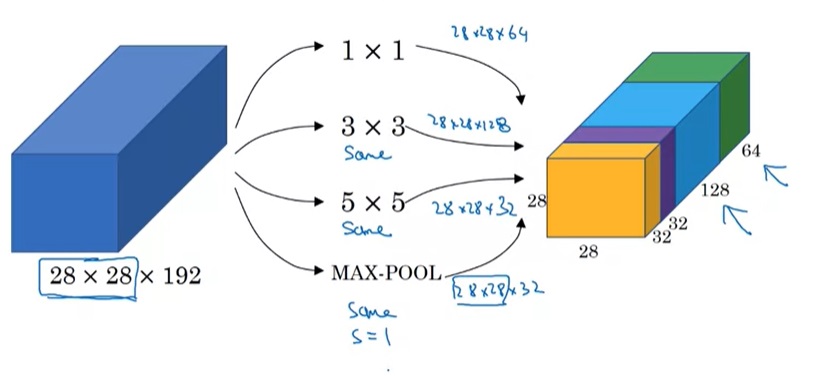
值得注意的是，这里的池化操作和我们之前见过的不太一样。为了保持输出张量的宽高，这个池化的步幅为1，且使用了等长填充。另外，为了调整池化操作输出的通道数，这条数据处理路线上还有一个用1x1卷积变换通道数的操作。这份图省略了很多这样的细节，下一节我们会见到这幅图的完整版。

在实现这样一种模块时，会碰到计算量过大的问题。比如把上面$28 \times 28 \times 192$的数据体用$5 \times 5$卷积卷成$28 \times 28 \times 32$的数据体，需要多少次乘法计算呢？对每个像素单独考虑，一个通道上的卷积要做$5 \times 5$此乘法，192个通道的卷积要做$192 \times 5 \times 5$次乘法。32个这样的卷积在$28 \times 28$的图片上要做$28 \times 28 \times 32 \times 192 \times 5 \times 5 \approx 120M$次乘法。这个计算量太大了。

为此，我们可以巧妙地先利用1x1卷积减少通道数，再做5x5卷积。这样，计算量就少得多了。

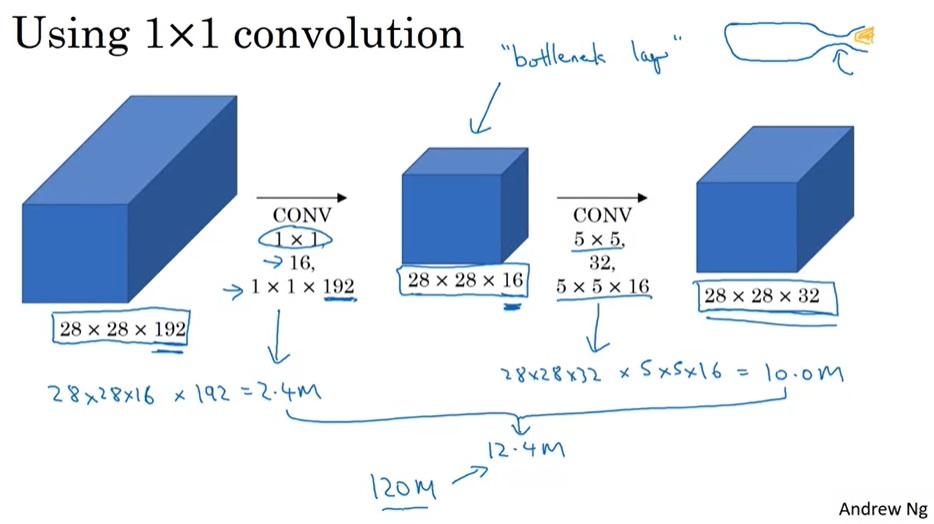
这样一种两头大，中间小的结构被形象地称为瓶颈(bottlenect)。这种结构被广泛用在许多典型网络中。

Inception网络

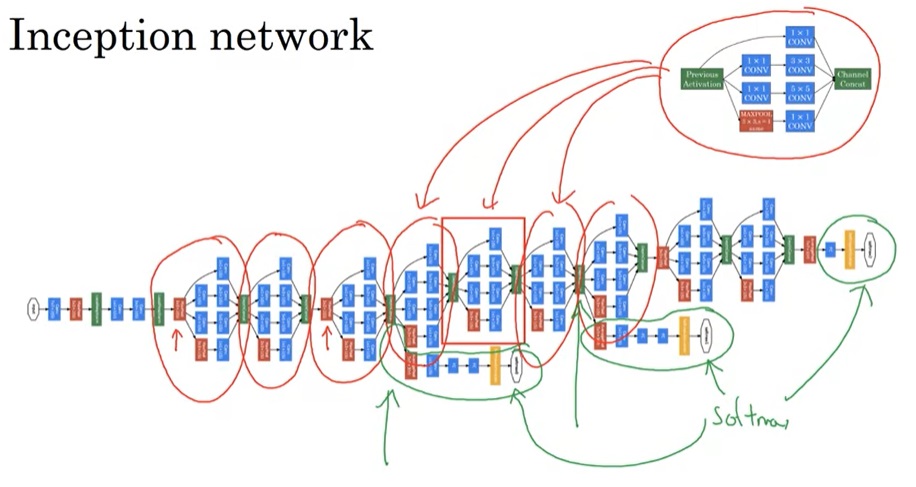
有了之前的知识，我们可以看Inception模块的完整结构了。1x1卷积没有什么特别的。为了减少3x3卷积和5x5卷积的计算量，做这两种卷积之前都会用1x1卷积减少通道数。而为了改变池化结果的通道数，池化后接了一个1x1卷积操作。

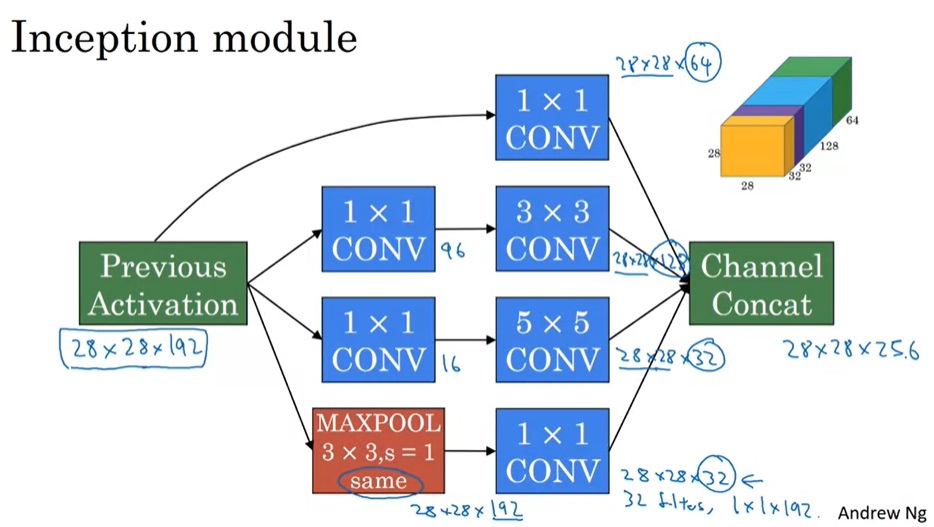
实际上，理解了Inception块，也就能看懂Inception网络了。如下图所示，红框内的模块都是Inception块。而这个网络还有一些小细节：除了和普通网络一样在网络的最后使用softmax输出结果外，这个网络还根据中间结果也输出了几个结果。当然，这些都是早期网络的设计技巧了。

MobileNet

MobileNet，顾名思义，这是一种适用于移动(mobile)设备的神经网络。移动设备的计算资源通常十分紧缺，因此，MobileNet对网络的计算量进行了极致的压缩。

减少卷积运算量

再回顾一遍，一次卷积操作中主要的计算量如下：

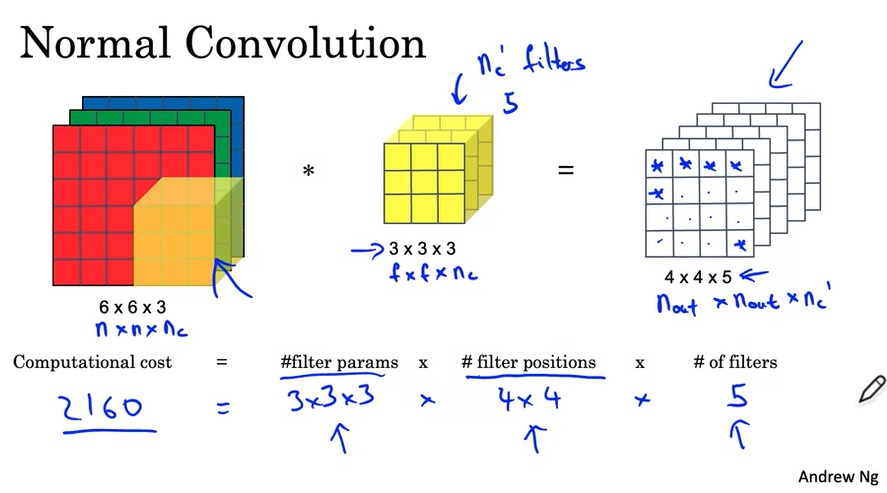
计算量这么大，主要问题出在每一个输出通道都要与每一个输入通道“全连接”上。为此，我们可以考虑让输出通道只由部分的输入通道决定。这样一种卷积的策略叫逐深度可分卷积(Depthwise Separable Convolution)。

这里的depthwise是“逐深度”的意思，但我觉得“逐通道”这个称呼会更容易理解一点。

逐深度可分卷积分为两步：逐深度卷积(depthwise convolution)，逐点卷积(pointwise convolution)。逐深度卷积生成新的通道，逐点卷积把各通道的信息关联起来。

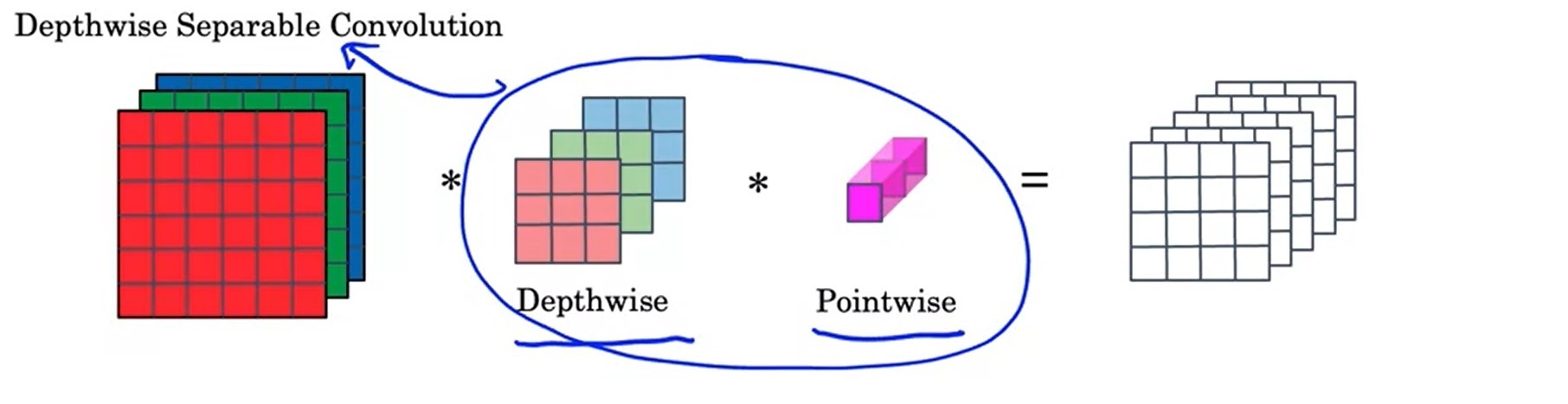
之前，要对下图中的三通道图片做卷积，需要3个卷积核分别处理3个通道。而在逐深度卷积中，我们只要1个卷积核。这个卷积核会把输入图像当成三个单通道图像来看待，分别对原图像的各个通道进行卷积，并生成3个单通道图像，最后把3个单通道图像拼回一个三通道图像。也就是说，逐深度卷积只能生成一幅通道数相同的新图像。

逐深度卷积可以通过设置卷积在编程框架中的groups参数来实现。参见我讲解卷积的文章。

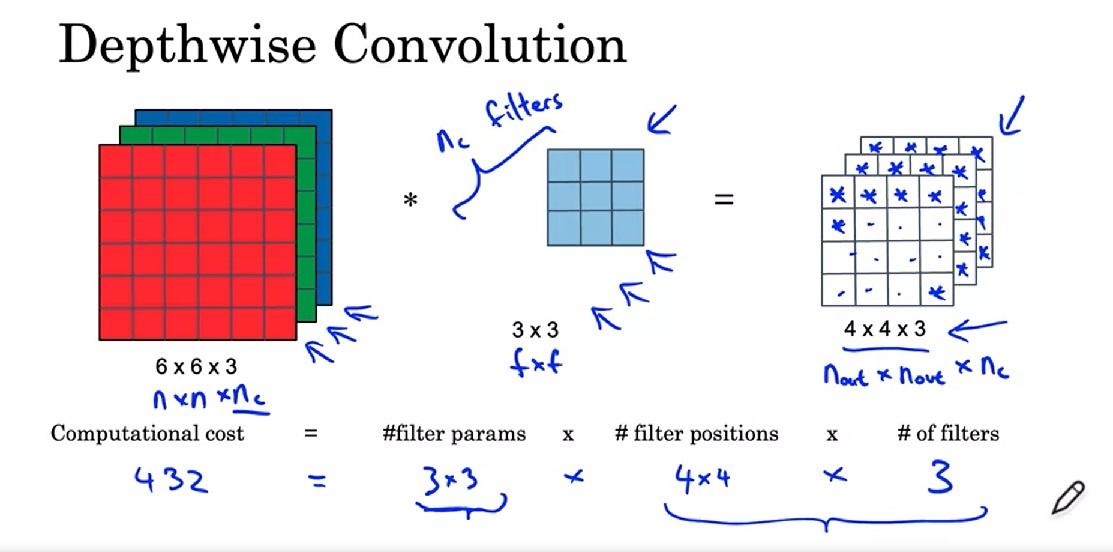
下一步，是逐点卷积，也就是1x1卷积。它用来改变图片的通道数。

之前的卷积有2160次乘法，现在只有432+240=672次，计算量确实减少了不少。实际上，优化后计算量占原计算量的比例是：

$$\frac{1}{n_c'} + \frac{1}{f^2}$$

其中$n_c’$是输出通道数，$f$是卷积核边长。一般来说计算量都会少10倍。

网络结构

知道了MobileNet的基本思想，我们来看几个不同版本的MobileNet。

MobileNet v1

13个逐深度可分卷积模块，之后接通常的池化、全连接、softmax。

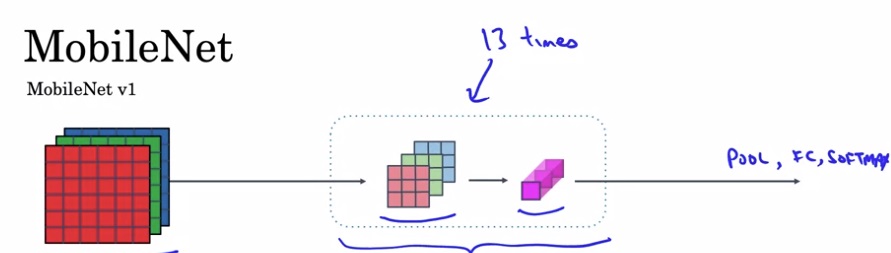
MobileNet v2

两个改进：

1. 残差连接
2. 扩张(expansion)操作

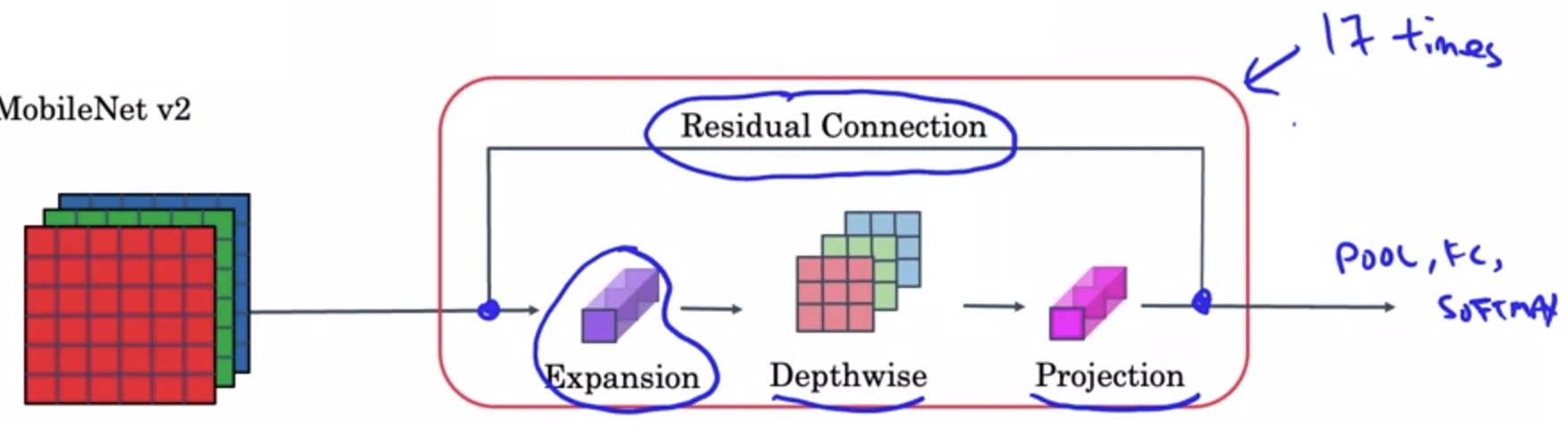
残差连接和ResNet一样。这里我们关注一下第二个改进。

在MobileNet v2中，先做一个扩张维度的1x1卷积，再做逐深度卷积，最后做之前的逐点1x1卷积。由于最后的逐点卷积起到的是减小维度的作用，所以最后一步操作也叫做投影。

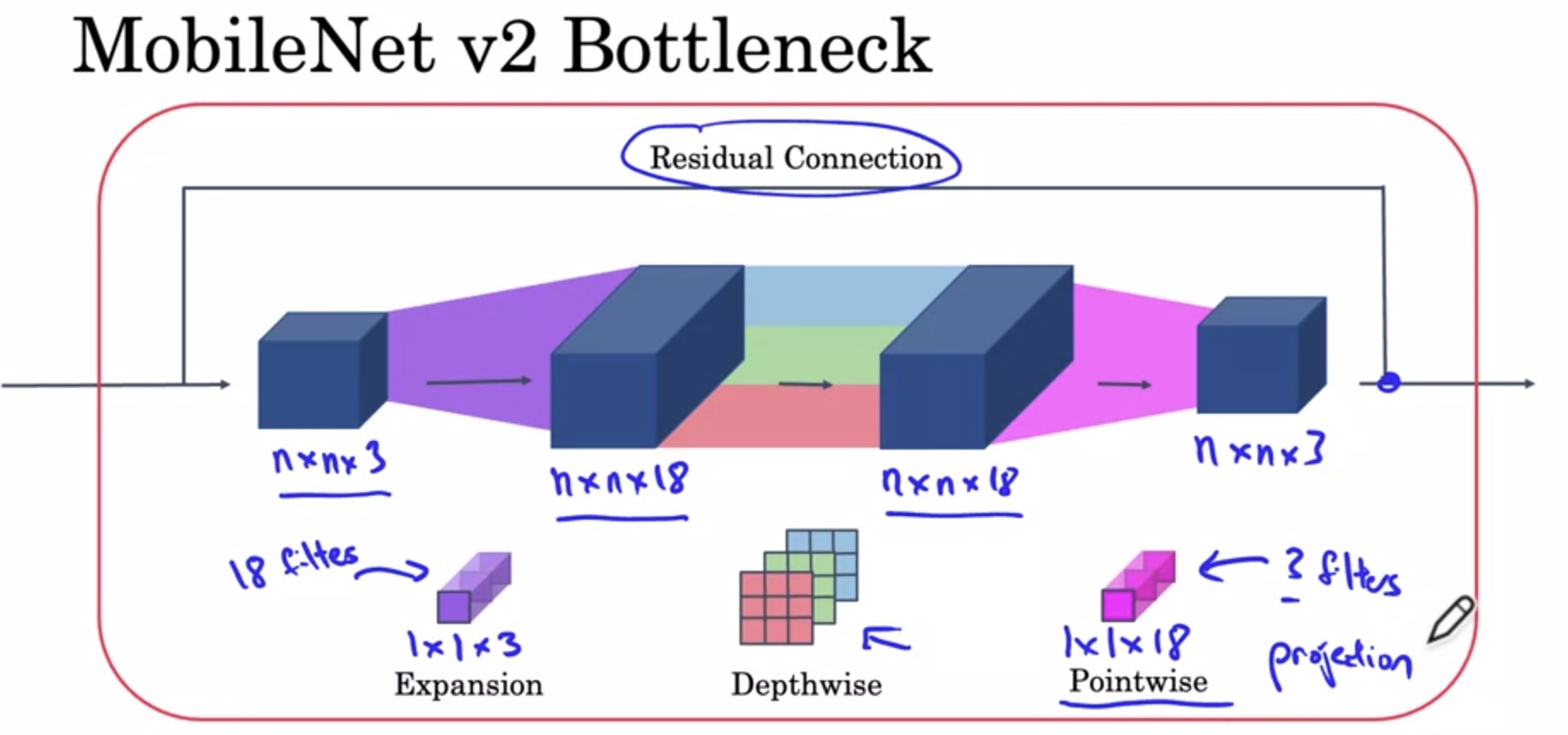
这种架构很好地解决了性能和效果之间的矛盾：在模块之间，数据的通道数只有3，占用内存少；在模块之内，更高通道的数据能拟合更复杂的函数。

EfficientNet

EfficientNet能根据设备的计算能力，自动调整网络占用的资源。

让我们想想，哪些因素决定了一个网络占用的运算资源？我们很快能想到下面这些因素：

• 图像分辨率
• 网络深度
• 特征的长度（即卷积核数量或神经元数量）

在EfficientNet中，我们可以在这三个维度上缩放网络，动态改变网络的计算量。EfficientNet的开源实现中，一般会提供各设备下的最优参数。

卷积网络实现细节

使用开源实现

由于深度学习项目涉及很多训练上的细节，想复现一个前人的工作是很耗时的。最好的学习方法是找到别人的开源代码，在现有代码的基础上学习。

深度学习的开源代码一般在GitHub上都能找到。如果是想看PyTorch实现，可以直接去GitHub上搜索OpenMMLab。

使用迁移学习

如第三门课第二周所学，我们可以用迁移学习，导入别人训练好的模型里的权重为初始权重，加速我们自己模型的训练。

还是以多分类任务的迁移学习为例（比如把一个1000分类的分类器迁移到一个猫、狗、其他的三分类模型上）。迁移后，新的网络至少要删除输出层，并按照新的多分类个数，重新初始化一个输出层。之后，根据新任务的数据集大小，冻结网络的部分参数，从导入的权重开始重新训练网络的其他部分：

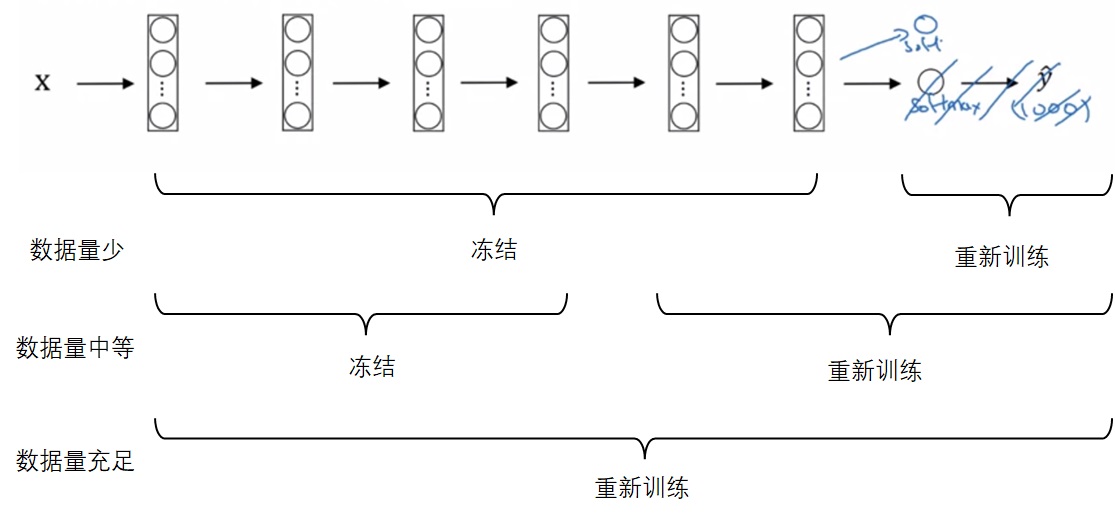
当然，可以多删除几个较深的层，也可以多加入几个除了输出层以外的隐藏层。

数据增强

由于CV任务总是缺少数据，数据增强是一种常见的提升网络性能的手段。

常见的改变形状的数据增强手段有：

• 镜像
• 裁剪
• 旋转
• 扭曲

此外，还可以改变图像的颜色。比如对三个颜色通道都随机加一个偏移量。

数据增强有一些实现上的细节：数据的读取及增强是放在CPU上运行的，训练是放在CPU或GPU上运行的。这两步其实是独立的，可以并行完成。最常见的做法是，在CPU上用多进程（发挥多核的优势）读取数据并进行数据增强，之后把数据搬到GPU上训练。

计算机视觉的现状与相关建议

一般来说，算法从两个来源获取知识：标注的数据，人工设计的特征。这二者是互补的关系。对于人工智能任务来说，如果有足够的数据，设计一个很简单的网络就行了；而如果数据量不足，则需要去精心设计网络结构。

像语音识别这种任务就数据充足，用简单的网络就行了。而大部分计算机视觉任务都处于数据不足的状态。哪怕计算机视觉中比较基础的图像分类任务，都需要设计结构复杂的网络，更不用说目标检测这些更难的任务了。

如果你想用深度学习模型参加刷精度的比赛，可以使用以下几个小技巧：

• 同时开始训练多个网络，算结果时取它们的平均值。
• 对图像分类任务，可以把图像随机裁剪一部分并输入网络，多次执行这一步骤并取平均分类结果。

也就是说，只是为了提高精度的话，可以想办法对同一份输入执行多次条件不同的推理，并对结果求平均。当然，实际应用中是不可能用性能这么低的方法。

总结

这节课是CNN中最重要的一节课。通过学习一些经典的CNN架构，我们掌握了很多有关搭建CNN的知识。总结一下：

• 早期CNN
  • 卷积、池化、全连接
  • 边长减小，通道数增加
• ResNet
  • 为什么使用ResNet？
  • 梯度问题是怎么被解决的？
  • 残差块的一般结构
  • 输入输出通道数不同的残差块
  • 了解ResNet的结构(ResNet-18, ResNet-50)
• Incpetion 网络
  • 1x1卷积
  • 用1x1卷积减少计算量
  • Inception网络的基本模块
• MobileNet
  • 逐深度可分卷积
  • MobileNet v2中的瓶颈结构

这节课介绍的都是比较前沿的CNN架构。在深度学习技术日新月异的今天，最好的学习方式是读论文，尽快一步一步跟上最新的技术。这堂课中提及的比较新的几篇论文，都有很高的阅读价值。

我打算在学完CNN的四周课后，暂时不去学第五门课，而是去阅读这些经典CNN论文并分享一下笔记。

在这周的代码实战里，我会分享一下如何用TensorFlow和PyTorch编写ResNet，同时介绍两种框架的进阶用法。