近两年,有许多图像生成类任务的前沿工作都使用了一种叫做”codebook”的机制。追溯起来,codebook机制最早是在VQ-VAE论文中提出的。相比于普通的VAE,VQ-VAE能利用codebook机制把图像编码成离散向量,为图像生成类任务提供了一种新的思路。VQ-VAE的这种建模方法启发了无数的后续工作,包括声名远扬的Stable Diffusion。
在这篇文章中,我将先以易懂的逻辑带领大家一步一步领悟VQ-VAE的核心思想,再介绍VQ-VAE中关键算法的具体形式,最后把VQ-VAE的贡献及其对其他工作的影响做一个总结。通过阅读这篇文章,你不仅能理解VQ-VAE本身的原理,更能知道如何将VQ-VAE中的核心机制活学活用。
从 AE 到 VQ-VAE
为什么VQ-VAE想要把图像编码成离散向量?让我们从最早的自编码器(Autoencoder, AE)开始一步一步谈起。AE是一类能够把图片压缩成较短的向量的神经网络模型,其结构如下图所示。AE包含一个编码器$e()$和一个解码器$d()$。在训练时,输入图像$\mathbf{x}$会被编码成一个较短的向量$\mathbf{z}$,再被解码回另一幅长得差不多的图像$\hat{\mathbf{x}}$。网络的学习目标是让重建出来的图像$\hat{\mathbf{x}}$和原图像$\mathbf{x}$尽可能相似。
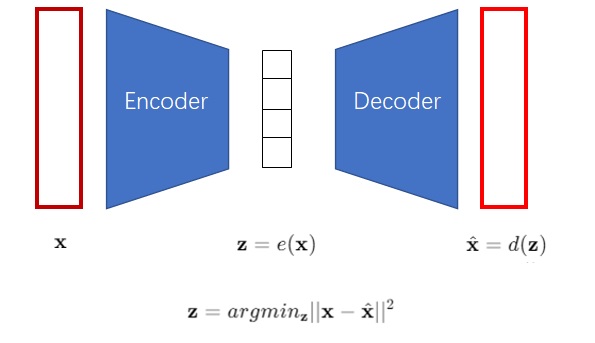
解码器可以把一个向量解码成图片。换一个角度看,解码器就是一个图像生成模型,因为它可以根据向量来生成图片。那么,AE可不可以用来做图像生成呢?很可惜,AE的编码器编码出来的向量空间是不规整的。也就是说,解码器只认识经编码器编出来的向量,而不认识其他的向量。如果你把自己随机生成出来的向量输入给解码器,解码器是生成不出有意义的图片的。AE不能够随机生成图片,所以它不能很好地完成图像生成任务,只能起到把图像压缩的作用。
AE离图像生成只差一步了。只要AE的编码空间比较规整,符合某个简单的数学分布(比如最常见的标准正态分布),那我们就可以从这个分布里随机采样向量,再让解码器根据这个向量来完成随机图片生成了。VAE就是这样一种改进版的AE。它用一些巧妙的方法约束了编码向量$\mathbf{z}$,使得$\mathbf{z}$满足标准正态分布。这样,解码器不仅认识编码器编出的向量,还认识其他来自标准正态分布的向量。训练完成后,我们就可以扔掉编码器,用来自标准正态分布的随机向量和解码器来实现随机图像生成了。
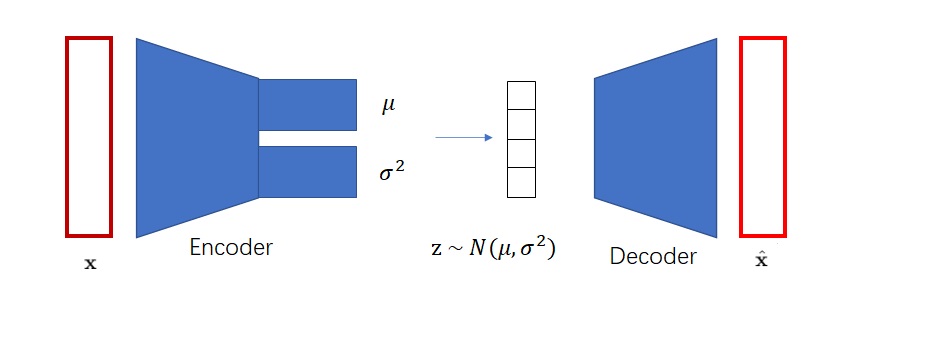
VAE的实现细节就不在这里赘述了,是否理解它对理解VQ-VAE没有影响。我们只需知道VAE可以把图片编码成符合标准正态分布的向量即可。让向量符合标准正态分布的原因是方便随机采样。同时,需要强调的是,VAE编码出来的向量是连续向量,也就是向量的每一维都是浮点数。如果把向量的某一维稍微改动0.0001,解码器还是认得这个向量,并且会生成一张和原向量对应图片差不多的图片。
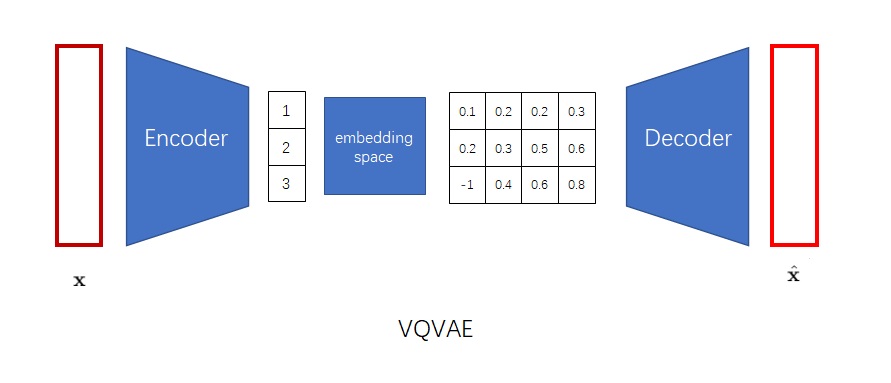
但是,VAE生成出来的图片都不是很好看。VQ-VAE的作者认为,VAE的生成图片之所以质量不高,是因为图片被编码成了连续向量。而实际上,把图片编码成离散向量会更加自然。比如我们想让画家画一个人,我们会说这个是男是女,年龄是偏老还是偏年轻,体型是胖还是壮,而不会说这个人性别是0.5,年龄是0.6,体型是0.7。因此,VQ-VAE会把图片编码成离散向量,如下图所示。
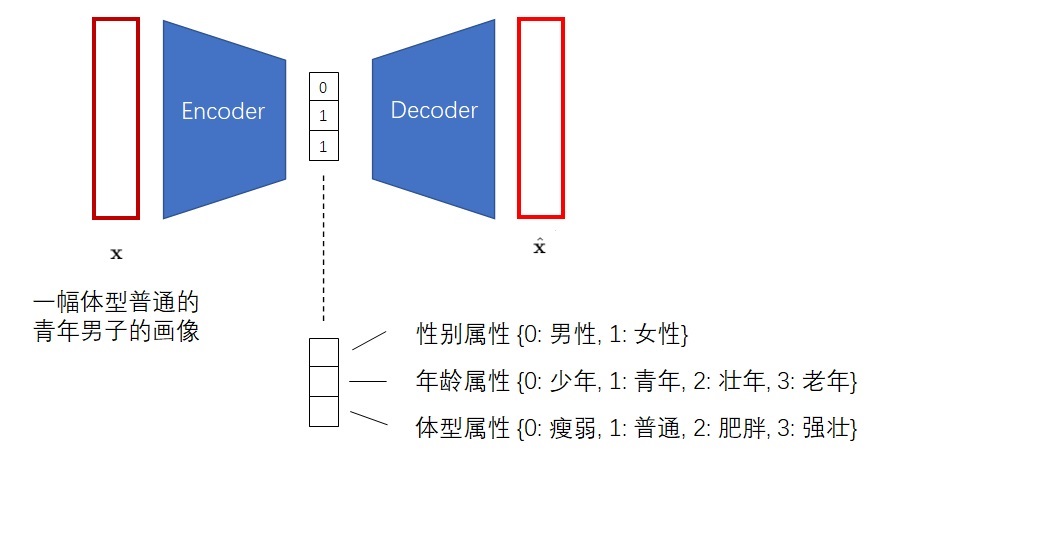
把图像编码成离散向量后,又会带来两个新的问题。第一个问题是,神经网络会默认输入满足一个连续的分布,而不善于处理离散的输入。如果你直接输入0, 1, 2这些数字,神经网络会默认1是一个处于0, 2中间的一种状态。为了解决这一问题,我们可以借鉴NLP中对于离散单词的处理方法。为了处理离散的输入单词,NLP模型的第一层一般都是词嵌入层,它可以把每个输入单词都映射到一个独一无二的连续向量上。这样,每个离散的数字都变成了一个特别的连续向量了。
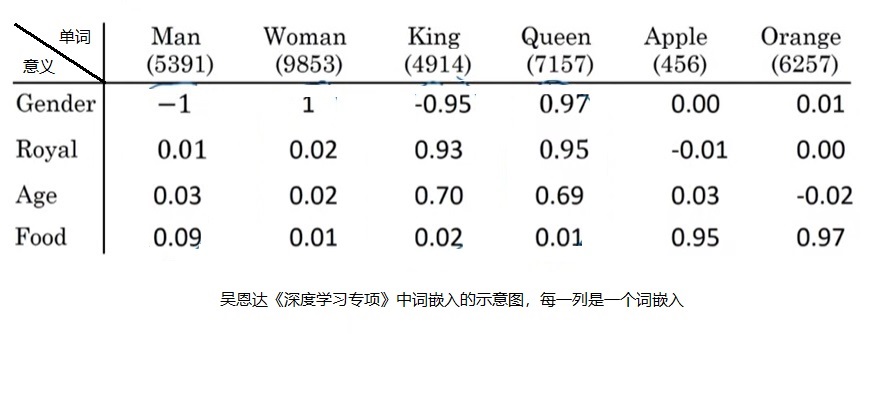
我们可以把类似的嵌入层加到VQ-VAE的解码器前。这个嵌入层在VQ-VAE里叫做”embedding space(嵌入空间)”,在后续文章中则被称作”codebook”。
离散向量的另一个问题是它不好采样。回忆一下,VAE之所以把图片编码成符合正态分布的连续向量,就是为了能在图像生成时把编码器扔掉,让随机采样出的向量也能通过解码器变成图片。现在倒好,VQ-VAE把图片编码了一个离散向量,这个离散向量构成的空间是不好采样的。VQ-VAE不是面临着和AE一样的问题嘛。
这个问题是无解的。没错!VQ-VAE根本不是一个图像生成模型。它和AE一样,只能很好地完成图像压缩,把图像变成一个短得多的向量,而不支持随机图像生成。VQ-VAE和AE的唯一区别,就是VQ-VAE会编码出离散向量,而AE会编码出连续向量。
可为什么VQ-VAE会被归类到图像生成模型中呢?这是因为VQ-VAE的作者利用VQ-VAE能编码离散向量的特性,使用了一种特别的方法对VQ-VAE的离散编码空间采样。VQ-VAE的作者之前设计了一种图像生成网络,叫做PixelCNN。PixelCNN能拟合一个离散的分布。比如对于图像,PixelCNN能输出某个像素的某个颜色通道取0~255中某个值的概率分布。这不刚好嘛,VQ-VAE也是把图像编码成离散向量。换个更好理解的说法,VQ-VAE能把图像映射成一个「小图像」。我们可以把PixelCNN生成图像的方法搬过来,让PixelCNN学习生成「小图像」。这样,我们就可以用PixelCNN生成离散编码,再利用VQ-VAE的解码器把离散编码变成图像。
让我们来整理一下VQ-VAE的工作过程。
- 训练VQ-VAE的编码器和解码器,使得VQ-VAE能把图像变成「小图像」,也能把「小图像」变回图像。
- 训练PixelCNN,让它学习怎么生成「小图像」。
- 随机采样时,先用PixelCNN采样出「小图像」,再用VQ-VAE把「小图像」翻译成最终的生成图像。
到这里,我们已经学完了VQ-VAE的核心思想。让我们来总结一下。VQ-VAE不是一个VAE,而是一个AE。它的目的是把图像压缩成离散向量。或者换个角度说,它提供了把大图像翻译成「小图像」的方法,也提供了把「小图像」翻译成大图像的方法。这样,一个随机生成大图像的问题,就被转换成了一个等价的随机生成一个较小的「图像」的问题。有一些图像生成模型,比如PixelCNN,更适合拟合离散分布。可以用它们来完成生成「小图像」的问题,填补上VQ-VAE生成图片的最后一片空缺。
VQ-VAE 设计细节
在上一节中,我们虽然认识了VQ-VAE的核心思想,但略过了不少实现细节,比如:
- VQ-VAE的编码器怎么输出离散向量。
- VQ-VAE怎么优化编码器和解码器。
- VQ-VAE怎么优化嵌入空间。
在这一节里,我们来详细探究这些细节。
输出离散编码
想让神经网络输出一个整数,最简单的方法是和多分类模型一样,输出一个Softmax过的概率分布。之后,从概率分布里随机采样一个类别,这个类别的序号就是我们想要的整数。比如在下图中,我们想得到一个由3个整数构成的离散编码,就应该让编码器输出3组logit,再经过Softmax与采样,得到3个整数。
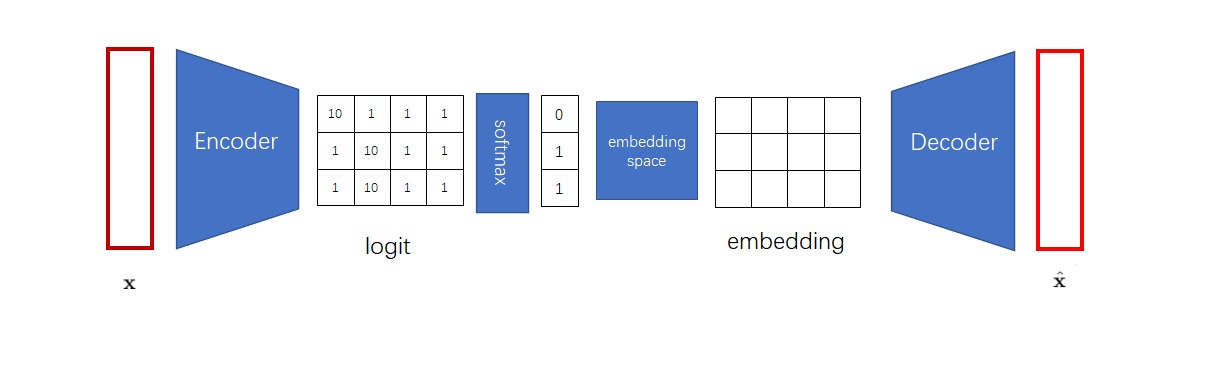
但是,这么做不是最高效的。得到离散编码后,下一步我们又要根据嵌入空间把离散编码转回一个向量。可见,获取离散编码这一步有一点多余。能不能把编码器的输出张量(它之前的名字叫logit)、解码器的输入张量embedding、嵌入空间直接关联起来呢?
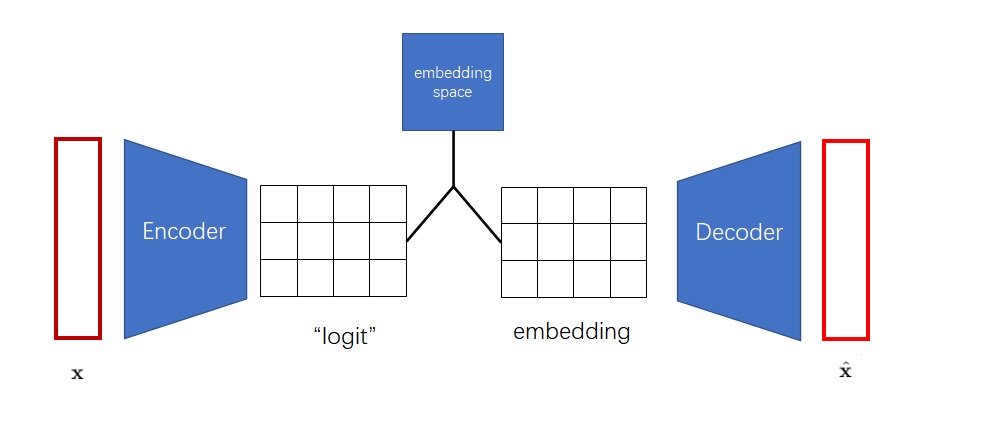
VQ-VAE使用了如下方式关联编码器的输出与解码器的输入:假设嵌入空间已经训练完毕,对于编码器的每个输出向量$z_e(x)$,找出它在嵌入空间里的最近邻$z_q(x)$,把$z_e(x)$替换成$z_q(x)$作为解码器的输入。
求最近邻,即先计算向量与嵌入空间$K$个向量每个向量的距离,再对距离数组取一个
argmin,求出最近的下标(比如图中的0, 1, 1),最后用下标去嵌入空间里取向量。下标构成的数组(比如图中的[0, 1, 1])也正是VQ-VAE的离散编码。
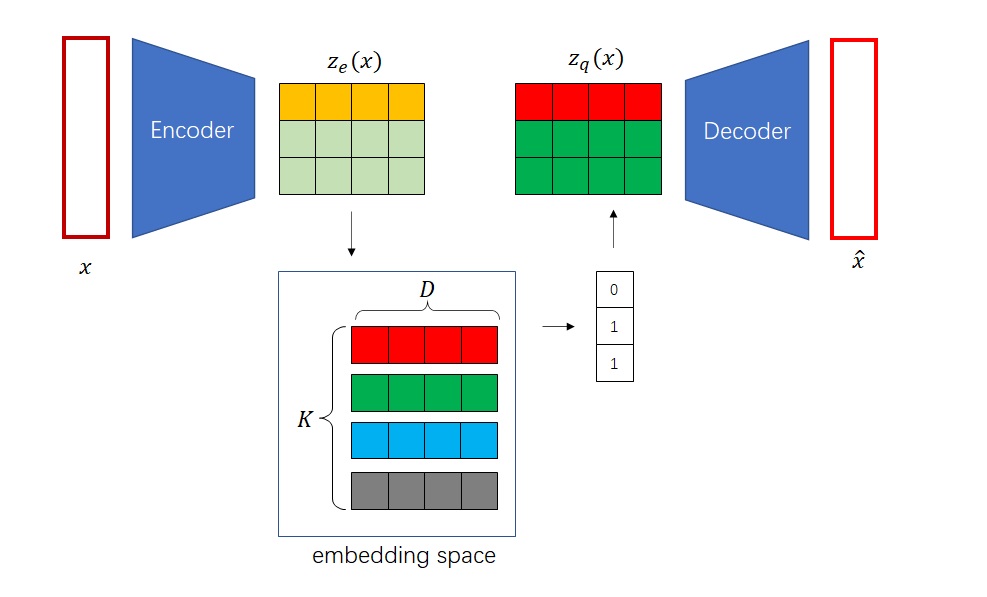
就这样,我们知道了VQ-VAE是怎么生成离散编码的。VQ-VAE的编码器其实不会显式地输出离散编码,而是输出了多个「假嵌入」$z_e(x)$。之后,VQ-VAE对每个$z_e(x)$在嵌入空间里找最近邻,得到真正的嵌入$z_q(x)$,把$z_q(x)$作为解码器的输入。
虽然我们现在能把编码器和解码器拼接到一起,但现在又多出了一个问题:怎么让梯度从解码器的输入$z_q(x)$传到$z_e(x)$?从$z_e(x)$到$z_q(x)$的变换是一个从数组里取值的操作,这个操作是求不了导的。我们在下一小节里来详细探究一下怎么优化VQ-VAE的编码器和解码器。
优化编码器和解码器
为了优化编码器和解码器,我们先来制订一下VQ-VAE的整体优化目标。由于VQ-VAE其实是一个AE,误差函数里应该只有原图像和目标图像的重建误差。
或者非要从VAE的角度说也行。VQ-VAE相当于输出了一个one-hot离散分布。假设输入图像$x$的离散编码$z$是$k$,则分布中仅有$q(z=k|x)=1$,$q(z=others|x)=0$。令离散编码$z$的先验分布是均匀分布(假设不知道输入图像$x$,每个离散编码取到的概率是等同的),则先验分布$q(z)$和后验分布$q(z|x)$的KL散度是常量。因此,KL散度项不用算入损失函数里。理解此处的数学推导意义不大,还不如直接理解成VQ-VAE其实是一个AE。
但直接拿这个误差来训练是不行的。误差中,$z_q(x)$是解码器的输入。从编码器输出$z_e(x)$到$z_q(x)$这一步是不可导的,误差无法从解码器传递到编码器上。要是可以把$z_q(x)$的梯度直接原封不动地复制到$z_e(x)$上就好了。
VQ-VAE使用了一种叫做”straight-through estimator”的技术来完成梯度复制。这种技术是说,前向传播和反向传播的计算可以不对应。你可以为一个运算随意设计求梯度的方法。基于这一技术,VQ-VAE使用了一种叫做$sg$(stop gradient,停止梯度)的运算:
也就是说,前向传播时,$sg$里的值不变;反向传播时,$sg$按值为0求导,即此次计算无梯度。(反向传播其实不会用到式子的值,只会用到式子的梯度。反向传播用到的loss值是在前向传播中算的)。
基于这种运算,我们可以设计一个把梯度从$z_e(x)$复制到$z_q(x)$的误差:
也就是说,前向传播时,就是拿解码器输入$z_q(x)$来算梯度。
而反向传播时,按下面这个公式求梯度,等价于把解码器的梯度全部传给$z_e(x)$。
这部分的PyTorch实现如下所示。在PyTorch里,(x).detach()就是$sg(x)$,它的值在前向传播时取x,反向传播时取0。
1 | L = x - decoder(z_e + (z_q - z_e).detach()) |
通过这一技巧,我们完成了梯度的传递,可以正常地训练编码器和解码器了。
优化嵌入空间
到目前为止,我们的讨论都是建立在嵌入空间已经训练完毕的前提上的。现在,我们来讨论一下嵌入空间的训练方法。
嵌入空间的优化目标是什么呢?嵌入空间的每一个向量应该能概括一类编码器输出的向量,比如一个表示「青年」的向量应该能概括所有14-35岁的人的照片的编码器输出。因此,嵌入空间的向量应该和其对应编码器输出尽可能接近。如下面的公式所示,$z_e(x)$是编码器的输出向量,$z_q(x)$是其在嵌入空间的最近邻向量。
但作者认为,编码器和嵌入向量的学习速度应该不一样快。于是,他们再次使用了停止梯度的技巧,把上面那个误差函数拆成了两部分。其中,$\beta$控制了编码器的相对学习速度。作者发现,算法对$\beta$的变化不敏感,$\beta$取0.1~2.0都差不多。
其实,在论文中,作者分别讨论了上面公式里的两个误差。第一个误差来自字典学习算法里的经典算法Vector Quantisation(VQ),也就是VQ-VAE里的那个VQ,它用于优化嵌入空间。第二个误差叫做专注误差,它用于约束编码器的输出,不让它跑到离嵌入空间里的向量太远的地方。
这样,VQ-VAE总体的损失函数可以写成:(由于算上了重建误差,我们多加一个$\alpha$用于控制不同误差之间的比例)
总结
VQ-VAE是一个把图像编码成离散向量的图像压缩模型。为了让神经网络理解离散编码,VQ-VAE借鉴了NLP的思想,让每个离散编码值对应一个嵌入,所有的嵌入都存储在一个嵌入空间(又称”codebook”)里。这样,VQ-VAE编码器的输出是若干个「假嵌入」,「假嵌入」会被替换成嵌入空间里最近的真嵌入,输入进解码器里。
VQ-VAE的优化目标由两部分组成:重建误差和嵌入空间误差。重建误差为输入图片和重建图片的均方误差。为了让梯度从解码器传到编码器,作者使用了一种巧妙的停止梯度算子,让正向传播和反向传播按照不同的方式计算。嵌入空间误差为嵌入和其对应的编码器输出的均方误差。为了让嵌入和编码器以不同的速度优化,作者再次使用了停止梯度算子,把嵌入的更新和编码器的更新分开计算。
训练完成后,为了实现随机图像生成,需要对VQ-VAE的离散分布采样,再把采样出来的离散向量对应的嵌入输入进解码器。VQ-VAE论文使用了PixelCNN来采样离散分布。实际上,PixelCNN不是唯一一种可用的拟合离散分布的模型。我们可以把它换成Transformer,甚至是diffusion模型。如果你当年看完VQ-VAE后立刻把PixelCNN换成了diffusion模型,那么恭喜你,你差不多提前设计出了Stable Diffusion。
可见,VQ-VAE最大的贡献是提供了一种图像压缩思路,把生成大图像的问题转换成了一个更简单的生成「小图像」的问题。图像压缩成离散向量时主要借助了嵌入空间,或者说”codebook”这一工具。这种解决问题的思路可以应用到所有图像生成类任务上,比如超分辨率、图像修复、图像去模糊等。所以近两年我们能看到很多使用了codebook的图像生成类工作。
参考资料
PixelCNN的介绍可以参见我之前的文章:详解PixelCNN大家族。
VQ-VAE的论文为Neural Discrete Representation Learning。这篇文章不是很好读懂,建议直接读我的这篇解读。再推荐另一份还不错的中文解读 https://www.spaces.ac.cn/archives/6760。