周弈帆的博客
0%

DDIM 简明讲解与 PyTorch 实现：加速扩散模型采样的通用方法

Posted on In ,

相比于多数图像生成模型，去噪扩散概率模型（Denoising Diffusion Probabilistic Model, DDPM）的采样速度非常慢。这是因为DDPM在采样时通常要做1000次去噪操作。但如果你玩过基于扩散模型的图像生成应用的话，你会发现，大多数应用只需要20次去噪即可生成图像。这是为什么呢？原来，这些应用都使用了一种更快速的采样方法——去噪扩散隐式模型（Denoising Diffusion Implicit Model, DDIM）。

基于DDPM，DDIM论文主要提出了两项改进。第一，对于一个已经训练好的DDPM，只需要对采样公式做简单的修改，模型就能在去噪时「跳步骤」，在一步去噪迭代中直接预测若干次去噪后的结果。比如说，假设模型从时刻$T=100$开始去噪，新的模型可以在每步去噪迭代中预测10次去噪操作后的结果，也就是逐步预测时刻$t=90, 80, …, 0$的结果。这样，DDPM的采样速度就被加速了10倍。第二，DDIM论文推广了DDPM的数学模型，从更高的视角定义了DDPM的前向过程（加噪过程）和反向过程（去噪过程）。在这个新数学模型下，我们可以自定义模型的噪声强度，让同一个训练好的DDPM有不同的采样效果。

在这篇文章中，我将言简意赅地介绍DDIM的建模方法，并给出我的DDIM PyTorch实现与实验结果。本文不会深究DDIM的数学推导，对这部分感兴趣的读者可以去阅读我在文末给出的参考资料。

回顾 DDPM

DDIM是建立在DDPM之上的一篇工作。在正式认识DDIM之前，我们先回顾一下DDPM中的一些关键内容，再从中引出DDIM的改进思想。

DDPM是一个特殊的VAE。它的编码器是$T$步固定的加噪操作，解码器是$T$步可学习的去噪操作。模型的学习目标是让每一步去噪操作尽可能抵消掉对应的加噪操作。

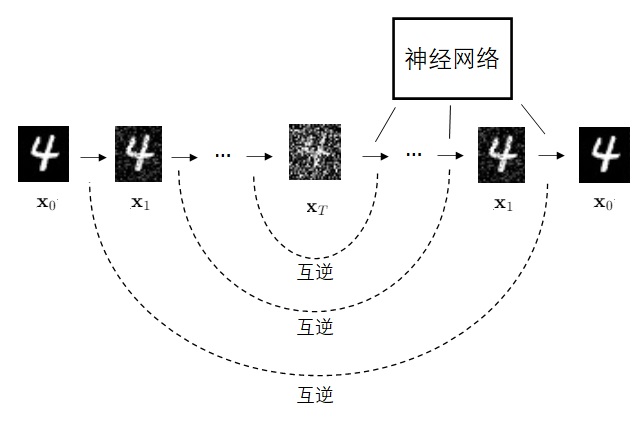
DDPM的加噪和去噪操作其实都是在某个正态分布中采样。因此，我们可以用概率$q, p$分别表示加噪和去噪的分布。比如 $q(\mathbf{x}_t|\mathbf{x}_{t-1})$ 就是由第 $t-1$ 时刻的图像到第 $t$ 时刻的图像的加噪声分布， $p(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ 就是由第 $t$ 时刻的图像到第 $t-1$ 时刻的图像的去噪声分布。这样，我们可以说网络的学习目标是让 $p(\mathbf{x}_{t-1} | \mathbf{x}_{t})$ 尽可能与 $q(\mathbf{x}_t | \mathbf{x}_{t-1})$ 和互逆。

但是，「互逆」并不是一个严格的数学表述。更具体地，我们应该让分布$p(\mathbf{x}_{t-1} | \mathbf{x}_{t})$和分布$q(\mathbf{x}_{t-1} | \mathbf{x}_{t})$尽可能相似。$q(\mathbf{x}_{t-1} | \mathbf{x}_{t})$和$p(\mathbf{x}_{t-1} | \mathbf{x}_{t})$的关系就和VAE中原图像与重建图像的关系一样。

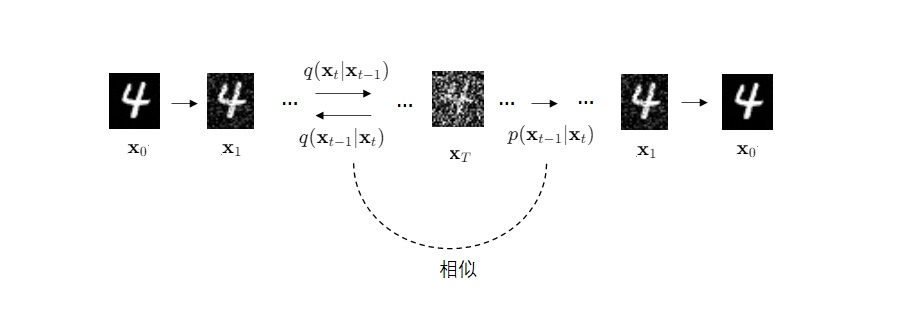
$q(\mathbf{x}_{t-1} | \mathbf{x}_{t})$是不好求得的，但在给定了输入数据$\mathbf{x}_{0}$时，$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})$是可以用贝叶斯公式求出来的：

我们不必关心具体的求解方法，只需要知道从等式右边的三项$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)、q(\mathbf{x}_{t-1} | \mathbf{x}_0)、q(\mathbf{x}_{t} | \mathbf{x}_0)$可以推导出等式左边的那一项。在DDPM中，$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1})$是一个定义好的式子，且$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}) = q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$。根据$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1})$，可以推出$q(\mathbf{x}_{t} | \mathbf{x}_0)$。知道了$q(\mathbf{x}_{t} | \mathbf{x}_0)$，$q(\mathbf{x}_{t-1} | \mathbf{x}_0)$也就知道了（把公式里的$t$换成$t-1$就行了）。这样，在DDPM中，等式右边的式子全部已知，等式左边的$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})$可以直接求出来。

上述推理过程可以简单地表示为：知道$q(\mathbf{x}_{t} | \mathbf{x}_0)$和$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$，就知道了神经网络的学习目标$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$。这几个公式在DDPM中的具体形式如下：

其中，只有参数$\beta_t$是可调的。$\bar{\alpha}_t$是根据$\beta_t$算出的变量，其计算方法为：$\alpha_t=1-\beta_t, \bar{\alpha}_t=\prod_{i=1}^t\alpha_i$。

由于学习目标$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$里只有一个未知变量$\mathbf{x}_0$，DDPM把学习目标简化成了只让神经网络根据$\mathbf{x}_{t}$拟合公式里的$\mathbf{x}_{0}$（更具体一点，是拟合从$\mathbf{x}_{0}$到$\mathbf{x}_{t}$的噪声）。也就是说，在训练时，$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$的公式不会被用到，只有$\mathbf{x}_{t}$和$\mathbf{x}_{0}$两个量之间的公式$q(\mathbf{x}_{t} | \mathbf{x}_0)$会被用到。只有在采样时，$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$的公式才会被用到。训练目标的推理过程可以总结为：

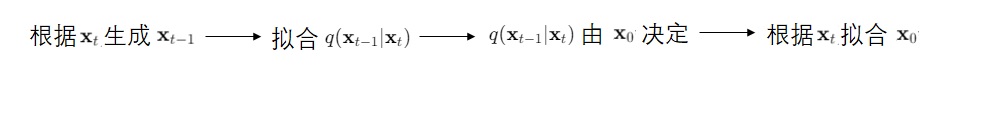
理解「DDPM的训练目标只有$\mathbf{x}_{0}$」对于理解DDIM非常关键。如果你在回顾DDPM时出现了问题，请再次阅读DDPM的相关介绍文章。

加速 DDPM

我们再次审视一下DDPM的推理过程：首先有$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}) = q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$。根据$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1})$，可以推出$q(\mathbf{x}_{t} | \mathbf{x}_0)$。知道$q(\mathbf{x}_{t} | \mathbf{x}_0)$和$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$，由贝叶斯公式，就知道了学习目标$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$。

根据这一推理过程，DDIM论文的作者想到，假如我们把贝叶斯公式中的$t$替换成$t_2$, $t-1$替换成$t_1$，其中$t_2$是比$t_1$大的任意某一时刻，那么我们不就可以从$t_2$到$t_1$跳步骤去噪了吗？比如令$t_2 = t_1 + 10$，我们就可以求出去除10次噪声的公式，去噪的过程就快了10倍。

修改之后，$q(\mathbf{x}_{t_1} | \mathbf{x}_0)$和$q(\mathbf{x}_{t_2} | \mathbf{x}_0)$依然很好求，只要把$t_1$, $t_2$代入普通的$q(\mathbf{x}_{t} | \mathbf{x}_0)$公式里就行。

但是，$q(\mathbf{x}_{t_2} | \mathbf{x}_{t_1}, \mathbf{x}_0)$怎么求呢？原来的$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t};\sqrt{1 - \beta_t}\mathbf{x}_{t - 1},\beta_t\mathbf{I})$来自于DDPM的定义，我们能直接把公式拿来用。能不能把$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$的公式稍微修改一下，让它兼容$q(\mathbf{x}_{t_2} | \mathbf{x}_{t_1}, \mathbf{x}_0)$呢？

修改$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$的思路如下：假如我们能把公式中的$\beta_t$换成一个由$t$和$t-1$决定的变量，我们就能把$t$换成$t_2$，$t-1$换成$t_1$，也就得到了$q(\mathbf{x}_{t_2} | \mathbf{x}_{t_1}, \mathbf{x}_0)$。

那怎么修改$\beta_t$的形式呢？很简单。我们知道$\beta_t$决定了$\bar{\alpha}_t$：$\alpha_t=1-\beta_t, \bar{\alpha}_t=\prod_{i=1}^t\alpha_i$。那么我们用$\bar{\alpha}_t$除以$\bar{\alpha}_{t-1}$，不就得到了$1-\beta_t$了吗？也就是说：

我们把这个用$\bar{\alpha}_t$和$\bar{\alpha}_{t-1}$表示的$\beta_t$套入$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$的公式里，再把$t$换成$t_2$，$t-1$换成$t_1$，就得到了$q(\mathbf{x}_{t_2} | \mathbf{x}_{t_1}, \mathbf{x}_0)$。有了这一项，贝叶斯公式等式右边那三项我们就全部已知，可以求出$q(\mathbf{x}_{t_1} | \mathbf{x}_{t_2}, \mathbf{x}_0)$，也就是可以一次性得到多个时刻后的去噪结果。

在这个过程中，我们只是把DDPM公式里的$\bar{\alpha}_t$换成$\bar{\alpha}_{t2}$，$\bar{\alpha}_{t-1}$换成$\bar{\alpha}_{t1}$，公式推导过程完全不变。网络的训练目标$\mathbf{x}_{0}$也没有发生改变，只是采样时的公式需要修改。这意味着我们可以先照着原DDPM的方法训练，再用这种更快速的方式采样。

我们之前只讨论了$t_1$到$t_2$为固定值的情况。实际上，我们不一定要间隔固定的时刻去噪一次，完全可以用原时刻序列的任意一个子序列来去噪。比如去噪100次的DDPM的去噪时刻序列为[99, 98, ..., 0]，我们可以随便取一个长度为10的子序列:[99, 98, 77, 66, 55, 44, 33, 22, 1, 0]，按这些时刻来去噪也能让采样速度加速10倍。但实践中没人会这样做，一般都是等间距地取时刻。

这样看来，在采样时，只有部分时刻才会被用到。那我们能不能顺着这个思路，干脆训练一个有效时刻更短（总时刻$T$不变）的DDPM，以加速训练呢？又或者保持有效训练时刻数不变，增大总时刻$T$呢？DDIM论文的作者提出了这些想法，认为这可以作为后续工作的研究方向。

从 DDPM 到 DDIM

除了加速DDPM外，DDIM论文还提出了一种更普遍的DDPM。在这种新的数学模型下，我们可以任意调节采样时的方差大小。让我们来看一下这个数学模型的推导过程。

DDPM的学习目标$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$由$q(\mathbf{x}_{t} | \mathbf{x}_0)$和$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$决定。具体来说，在求解正态分布$q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_0)$时，我们会将它的均值$\tilde{\mu}_t$和方差$\tilde{\beta}_t$设为未知量，并将条件$q(\mathbf{x}_{t} | \mathbf{x}_0)$、$q(\mathbf{x}_{t-1} | \mathbf{x}_0)$、$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$代入，求解出确定的$\tilde{\mu}_t$和$\tilde{\beta}_t$。

在上文我们分析过，DDPM训练时只需要拟合$\mathbf{x}_0$，只需要用到$\mathbf{x}_0$和$\mathbf{x}_t$的关系$q(\mathbf{x}_{t} | \mathbf{x}_0)$。在不修改训练过程的前提下，我们能不能把限制$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$去掉（即$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$可以是任意一个正态分布，而不是我们提前定义好的一个正态分布），得到一个更普遍的DDPM呢？

这当然是可以的。根据基础的解方程知识，我们知道，去掉一个方程后，会多出一个自由变量。取消了$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$的限制后，均值$\tilde{\mu}_t$和方差$\tilde{\beta}_t$就不能同时确定下来了。我们可以令方差$\tilde{\beta}_t$为自由变量，并让$\tilde{\mu}_t$用含$\tilde{\beta}_t$的式子表示出来。这样，我们就得到了一个方差可变的更一般的DDPM。

让我们来看一下这个新模型的具体公式。原来的DDPM的加噪声逆操作的分布为：

新的分布公式为：

新公式是旧公式的一个推广版本。如果我们把DDPM的方差$(1-\bar{\alpha}_{t-1})/(1 - \bar{\alpha}_{t}) \cdot \beta_t$代入新公式里的$\tilde{\beta}_t$，就能把新公式还原成DDPM的公式。和DDPM的公式一样，我们也可以把$\mathbf{x}_{0}$拆成$\mathbf{x}_{t}$和噪声$\epsilon$表示的式子。

现在采样时方差可以随意取了，我们来讨论一种特殊的方差取值——$\tilde{\beta}_t=0$。也就是说，扩散模型的反向过程变成了一个没有噪声的确定性过程。给定随机噪声$\mathbf{x}_{T}$，我们只能得到唯一的采样结果$\mathbf{x}_{0}$。这种结果确定的概率模型被称为隐式概率模型（implicit probabilistic model）。所以，论文作者把方差为0的这种扩散模型称为DDIM（Denoising Diffusion Implicit Model）。

为了方便地选取方差值，作者将方差改写为

其中，$\eta\in[0, 1]$。通过选择不同的$\eta$，我们实际上是在DDPM和DDIM之间插值。$\eta$控制了插值的比例。$\eta=0$，模型是DDIM；$\eta=1$，模型是DDPM。

除此之外，DDPM论文曾在采样时使用了另一种方差取值：$\tilde{\beta}_t=\beta_t$，即去噪方差等于加噪方差。实验显示这个方差的采样结果还不错。我们可以把这个取值也用到DDIM论文提出的方法里，只不过这个方差值不能直接套进上面的公式。在代码实现部分我会介绍该怎么在DDIM方法中使用这个方差。

注意，在这一节的推导过程中，我们依然没有修改DDPM的训练目标。我们可以把这种的新的采样方法用在预训练的DDPM上。当然，我们可以在使用新的采样方法的同时也使用上一节的加速采样方法。

实验

到这里为止，我们已经学完了DDIM论文的两大内容：加速采样、更换采样方差。加速采样的意义很好理解，它能大幅减少采样时间。可更换采样方差有什么意义呢？我们看完论文中的实验结果就知道了。

论文展示了新采样方法在不同方差、不同采样步数下的FID指标（越小越好）。其中，$\hat{\sigma}$表示使用DDPM中的$\tilde{\beta}_t=\beta_t$方差取值。实验结果非常有趣。在使用采样加速（步数比总时刻1000要小）时，$\eta=0$的DDIM的表现最好，而$\hat{\sigma}$的情况则非常差。而当$\eta$增大，模型越来越靠近DDPM时，用$\hat{\sigma}$的结果会越来越好。而在DDPM中，用$\hat{\sigma}$的结果是最好的。

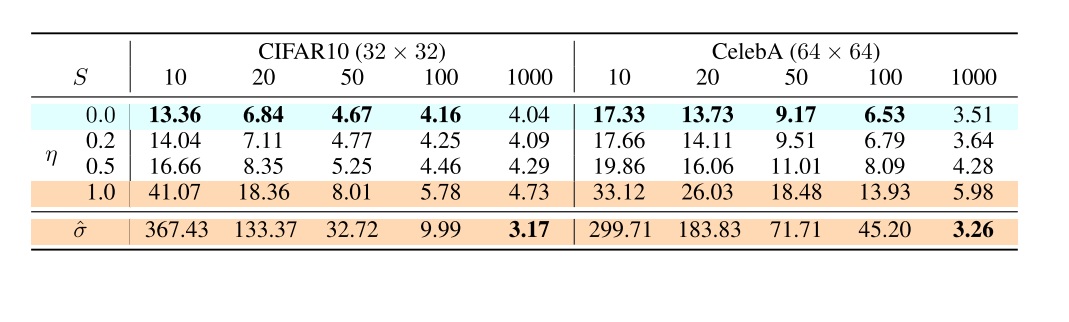
从这个实验结果中，我们可以得到一条很简单的实践指南：如果使用了采样加速，一定要用效果最好的DDIM；而使用原DDPM的话，可以维持原论文提出的$\tilde{\beta}_t=\beta_t$方差取值。

总结

DDIM论文提出了DDPM的两个拓展方向：加速采样、变更采样方差。通过同时使用这两个方法，我们能够在不重新训练DDPM、尽可能不降低生成质量的前提下，让扩散模型的采样速度大幅提升（一般可以快50倍）。让我们再从头理一理提出DDIM方法的思考过程。

为了能直接使用预训练的DDPM，我们希望在改进DDPM时不更改DDPM的训练过程。而经过简化后，DDPM的训练目标只有拟合$\mathbf{x}_{0}$，训练时只会用到前向过程公式$q(\mathbf{x}_{t} | \mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t}; \sqrt{\bar{\alpha}_t}\mathbf{x}_{0}, (1-\bar{\alpha}_t)\mathbf{I})$。所以，我们的改进应该建立在公式$q(\mathbf{x}_{t} | \mathbf{x}_0)$完全不变的前提下。

通过对DDPM反向过程公式的简单修改，也就是把$t$改成$t_2$，$t-1$改成$t_1$，我们可以把去噪一步的公式改成去噪多步的公式，以大幅加速DDPM。可是，这样改完之后，采样的质量会有明显的下降。

我们可以猜测，减少了采样迭代次数后，采样质量之所以下降，是因为每次估计的去噪均值更加不准确。而每次去噪迭代中的噪声（由方差项决定的那一项）放大了均值的不准确性。我们能不能干脆让去噪时的方差为0呢？为了让去噪时的方差可以自由变动，我们可以去掉DDPM的约束条件。由于贝叶斯公式里的$q(\mathbf{x}_{t} | \mathbf{x}_0)$不能修改，我们只能去掉$q(\mathbf{x}_{t} | \mathbf{x}_{t - 1}, \mathbf{x}_0)$的限制。去掉限制后，方差就成了自由变量。我们让去噪方差为0，让采样过程没有噪声。这样，就得到了本文提出的DDIM模型。实验证明，在采样迭代次数减少后，使用DDIM的生成结果是最优的。

在本文中，我较为严格地区分了DDPM和DDIM的叫法：DDPM指DDPM论文中提出的有1000个扩散时刻的模型，它的采样方差只有两种取值（$\tilde{\beta}_t=(1-\bar{\alpha}_{t-1})/(1 - \bar{\alpha}_{t}) \cdot \beta_t$, $\tilde{\beta}_t=\beta_t$）。DDIM指DDIM论文中提出的$\eta=0$的推广版DDPM模型。DDPM和DDIM都可以使用采样加速。但是，从习惯上我们会把没有优化加速的DDPM称为”DDPM”，把$\eta$可以任取，采样迭代次数可以任取的采样方法统称为”DDIM”。一些开源库中会有叫DDIMSampler的类，调节$\eta$的参数大概会命名为eta，调节迭代次数的参数大概会命名为ddim_num_steps。一般我们令eta=0，ddim_num_steps=20即可。

DDIM的代码实现没有太多的学习价值，只要在DDPM代码的基础上把新数学公式翻译成代码即可。其中唯一值得注意的就是如何在DDIM中使用DDPM的方差$\tilde{\beta}_t=\beta_t$。对此感兴趣的话可以阅读我接下来的代码实现介绍。

在这篇解读中，我略过了DDIM论文中的大部分数学推导细节。对DDIM数学模型的推导过程感兴趣的话，可以阅读我在参考文献中推荐的文章，或者看一看原论文。

DDIM PyTorch 实现

在这个项目中，我们将对一个在CelebAHQ上预训练的DDPM执行DDIM采样，尝试复现论文中的那个FID表格，以观察不同eta和ddim_steps对于采样结果的影响。

代码仓库：https://github.com/SingleZombie/DL-Demos/tree/master/dldemos/ddim

DDPM 基础项目

DDIM只是DDPM的一种采样改进策略。为了复现DDIM的结果，我们需要一个DDPM基础项目。由于DDPM并不是本文的重点，在这一小节里我将简要介绍我的DDPM实现代码的框架。

我们的实验需要使用CelebAHQ数据集，请在 https://www.kaggle.com/datasets/badasstechie/celebahq-resized-256x256 下载该数据集并解压到项目的data/celebA/celeba_hq_256目录下。另外，我在Hugging Face上分享了一个在64x64 CelebAHQ上训练的DDPM模型：https://huggingface.co/SingleZombie/dldemos/tree/main/ckpt/ddim ，请把它放到项目的dldemos/ddim目录下。

先运行dldemos/ddim/dataset.py下载MNIST，再直接运行dldemos/ddim/main.py，代码会自动完成MNIST上的训练，并执行步数1000的两种采样和步数20的三种采样，同时将结果保存在目录work_dirs中。以下是我得到的MNIST DDPM采样结果（存储在work_dirs/diffusion_ddpm_sigma_hat.jpg中）。

为了查看64x64 CelebAHQ上的采样结果，可以在dldemos/ddim/main.py的main函数里把config_id改成2，再注释掉训练函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 0 for MNIST. See configs.py
config_id = 2
cfg = configs[config_id]
n_steps = 1000
device = 'cuda'
model_path = cfg['model_path']
img_shape = cfg['img_shape']
to_bgr = False if cfg['dataset_type'] == 'MNIST' else True

net = UNet(n_steps, img_shape, cfg['channels'], cfg['pe_dim'],
           cfg.get('with_attn', False), cfg.get('norm_type', 'ln'))
ddpm = DDPM(device, n_steps)

# train(ddpm,
#       net,
#       cfg['dataset_type'],
#       resolution=(img_shape[1], img_shape[2]),
#       batch_size=cfg['batch_size'],
#       n_epochs=cfg['n_epochs'],
#       device=device,
#       ckpt_path=model_path)

以下是我得到的CelebAHQ DDPM采样结果（存储在work_dirs/diffusion_ddpm_sigma_hat.jpg中）。

项目目录下的configs.py存储了训练配置，dataset.py定义了DataLoader，network.py定义了U-Net的结构，ddpm.py和ddim.py分别定义了普通的DDPM前向过程和采样以及DDIM采样，dist_train.py提供了并行训练脚本，dist_sample.py提供了并行采样脚本，main.py提供了单卡运行的所有任务脚本。

在这个项目中，我们的主要的目标是基于其他文件，编写ddim.py。我们先来看一下原来的DDPM类是怎么实现的，再仿照它的接口写一个DDIM类。

实现 DDIM 采样

在我的设计中，DDPM类不是一个神经网络（torch.nn.Module），它仅仅维护了扩散模型的alpha等变量，并描述了前向过程和反向过程。

在DDPM类中，我们可以在初始化函数里定义好要用到的self.betas, self.alphas, self.alpha_bars变量。如果在工程项目中，我们可以预定义好更多的常量以节约采样时间。但在学习时，我们可以少写一点代码，让项目更清晰一点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class DDPM():

    def __init__(self,
                 device,
                 n_steps: int,
                 min_beta: float = 0.0001,
                 max_beta: float = 0.02):
        betas = torch.linspace(min_beta, max_beta, n_steps).to(device)
        alphas = 1 - betas
        alpha_bars = torch.empty_like(alphas)
        product = 1
        for i, alpha in enumerate(alphas):
            product *= alpha
            alpha_bars[i] = product
        self.betas = betas
        self.n_steps = n_steps
        self.alphas = alphas
        self.alpha_bars = alpha_bars

前向过程就是把正态分布的公式$q(\mathbf{x}_{t} | \mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t}; \sqrt{\bar{\alpha}_t}\mathbf{x}_{0}, (1-\bar{\alpha}_t)\mathbf{I})$翻译一下。

1
2
3
4
5
6
def sample_forward(self, x, t, eps=None):
    alpha_bar = self.alpha_bars[t].reshape(-1, 1, 1, 1)
    if eps is None:
        eps = torch.randn_like(x)
    res = eps * torch.sqrt(1 - alpha_bar) + torch.sqrt(alpha_bar) * x
    return res

在反向过程中，我们从self.n_steps到1枚举时刻t（代码中时刻和数组下标有1的偏差），按照公式算出每一步的去噪均值和方差，执行去噪。算法流程如下：

参数simple_var=True表示令方差$\sigma_t^2=\beta_t$，而不是$(1-\bar{\alpha}_{t-1})/(1 - \bar{\alpha}_{t}) \cdot \beta_t$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def sample_backward(self, img_or_shape, net, device, simple_var=True):
    if isinstance(img_or_shape, torch.Tensor):
        x = img_or_shape
    else:
        x = torch.randn(img_or_shape).to(device)
    net = net.to(device)
    for t in tqdm(range(self.n_steps - 1, -1, -1), "DDPM sampling"):
        x = self.sample_backward_step(x, t, net, simple_var)

    return x

def sample_backward_step(self, x_t, t, net, simple_var=True):

    n = x_t.shape[0]
    t_tensor = torch.tensor([t] * n,
                            dtype=torch.long).to(x_t.device).unsqueeze(1)
    eps = net(x_t, t_tensor)

    if t == 0:
        noise = 0
    else:
        if simple_var:
            var = self.betas[t]
        else:
            var = (1 - self.alpha_bars[t - 1]) / (
                1 - self.alpha_bars[t]) * self.betas[t]
        noise = torch.randn_like(x_t)
        noise *= torch.sqrt(var)

    mean = (x_t -
            (1 - self.alphas[t]) / torch.sqrt(1 - self.alpha_bars[t]) *
            eps) / torch.sqrt(self.alphas[t])
    x_t = mean + noise

    return x_t

接下来，我们来实现DDIM类。DDIM是DDPM的推广，我们可以直接用DDIM类继承DDPM类。它们共享初始化函数与前向过程函数。

1
2
3
4
5
6
7
8
class DDIM(DDPM):

    def __init__(self,
                 device,
                 n_steps: int,
                 min_beta: float = 0.0001,
                 max_beta: float = 0.02):
        super().__init__(device, n_steps, min_beta, max_beta)

我们要修改的只有反向过程的实现函数。整个函数的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def sample_backward(self,
                    img_or_shape,
                    net,
                    device,
                    simple_var=True,
                    ddim_step=20,
                    eta=1):
    if simple_var:
        eta = 1
    ts = torch.linspace(self.n_steps, 0,
                        (ddim_step + 1)).to(device).to(torch.long)
    if isinstance(img_or_shape, torch.Tensor):
        x = img_or_shape
    else:
        x = torch.randn(img_or_shape).to(device)
    batch_size = x.shape[0]
    net = net.to(device)
    for i in tqdm(range(1, ddim_step + 1),
                  f'DDIM sampling with eta {eta} simple_var {simple_var}'):
        cur_t = ts[i - 1] - 1
        prev_t = ts[i] - 1

        ab_cur = self.alpha_bars[cur_t]
        ab_prev = self.alpha_bars[prev_t] if prev_t >= 0 else 1

        t_tensor = torch.tensor([cur_t] * batch_size,
                                dtype=torch.long).to(device).unsqueeze(1)
        eps = net(x, t_tensor)
        var = eta * (1 - ab_prev) / (1 - ab_cur) * (1 - ab_cur / ab_prev)
        noise = torch.randn_like(x)

        first_term = (ab_prev / ab_cur)**0.5 * x
        second_term = ((1 - ab_prev - var)**0.5 -
                        (ab_prev * (1 - ab_cur) / ab_cur)**0.5) * eps
        if simple_var:
            third_term = (1 - ab_cur / ab_prev)**0.5 * noise
        else:
            third_term = var**0.5 * noise
        x = first_term + second_term + third_term

    return x

我们来把整个函数过一遍。先看一下函数的参数。相比DDPM，DDIM的采样会多出两个参数：ddim_step, eta。如正文所述，ddim_step表示执行几轮去噪迭代，eta表示DDPM和DDIM的插值系数。

1
2
3
4
5
6
7
def sample_backward(self,
                    img_or_shape,
                    net,
                    device,
                    simple_var=True,
                    ddim_step=20,
                    eta=1):

在开始迭代前，要做一些预处理。根据论文的描述，如果使用了DDPM的那种简单方差，一定要令eta=1。所以，一开始我们根据simple_var对eta做一个处理。之后，我们要准备好迭代时用到的时刻。整个迭代过程中，我们会用到从self.n_steps到0等间距的ddim_step+1个时刻（self.n_steps是初始时刻，不在去噪迭代中）。比如总时刻self.n_steps=100，ddim_step=10，ts数组里的内容就是[100, 90, 80, 70, 60, 50, 40, 30, 20, 10, 0]。

1
2
3
4
5
6
7
8
9
10
if simple_var:
    eta = 1
ts = torch.linspace(self.n_steps, 0,
                    (ddim_step + 1)).to(device).to(torch.long)
if isinstance(img_or_shape, torch.Tensor):
    x = img_or_shape
else:
    x = torch.randn(img_or_shape).to(device)
batch_size = x.shape[0]
net = net.to(device)

做好预处理后，进入去噪循环。在for循环中，我们从1到ddim_step遍历ts的下标，从时刻数组ts里取出较大的时刻cur_t（正文中的$t_2$）和较小的时刻prev_t（正文中的$t_1$）。由于self.alpha_bars存储的是t=1, t=2, ..., t=n_steps时的变量，时刻和数组下标之间有一个1的偏移，我们要把ts里的时刻减去1得到时刻在self.alpha_bars里的下标，再取出对应的变量ab_cur, ab_prev。注意，在当前时刻为0时，self.alpha_bars是没有定义的。但由于self.alpha_bars表示连乘，我们可以特别地令当前时刻为0（prev_t=-1）时的alpha_bar=1。

1
2
3
4
5
6
7
for i in tqdm(range(1, ddim_step + 1),
              f'DDIM sampling with eta {eta} simple_var {simple_var}'):
    cur_t = ts[i - 1] - 1
    prev_t = ts[i] - 1

    ab_cur = self.alpha_bars[cur_t]
    ab_prev = self.alpha_bars[prev_t] if prev_t >= 0 else 1

准备好时刻后，我们使用和DDPM一样的方法，用U-Net估计生成x_t时的噪声eps，并准备好DDPM采样算法里的噪声noise（公式里的$\mathbf{z}$）。
与DDPM不同，在计算方差var时（公式里的$\sigma_t^2$），我们要给方差乘一个权重eta。

1
2
3
4
5
t_tensor = torch.tensor([cur_t] * batch_size,
                        dtype=torch.long).to(device).unsqueeze(1)
eps = net(x, t_tensor)
var = eta * (1 - ab_prev) / (1 - ab_cur) * (1 - ab_cur / ab_prev)
noise = torch.randn_like(x)

接下来，我们要把之前算好的所有变量用起来，套入DDIM的去噪均值计算公式中。

也就是(设$\sigma_t^2 = \tilde{\beta}_t$, $\mathbf{z}$为来自标准正态分布的噪声)：

由于我们只有噪声$\epsilon$，要把$\mathbf{x}_0=(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t}\epsilon)/\sqrt{\bar{\alpha}_t}$代入，得到不含$\mathbf{x}_0$的公式：

我在代码里把公式的三项分别命名为first_term, second_term, third_term，以便查看。

特别地，当使用DDPM的$\hat{\sigma_t}$方差取值（令$\sigma_t^2=\beta_t=\hat{\sigma_t}^2$）时，不能把这个方差套入公式中，不然$\sqrt{1-{\bar{\alpha}}_{t}-\sigma_t^2}$的根号里的数会小于0。DDIM论文提出的做法是，只修改后面和噪声$\mathbf{z}$有关的方差项，前面这个根号里的方差项保持$\sigma_t^2=(1-\bar{\alpha}_{t-1})/(1 - \bar{\alpha}_{t}) \cdot \beta_t$ ($\eta=1$)的取值。

当然，上面这些公式全都是在描述$t$到$t-1$。当描述$t_2$到$t_1$时，只需要把$\beta_t$换成$1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$，再把所有$t$换成$t_2$，$t-1$换成$t_1$即可。

把上面的公式和处理逻辑翻译成代码，就是这样：

1
2
3
4
5
6
7
8
first_term = (ab_prev / ab_cur)**0.5 * x
second_term = ((1 - ab_prev - var)**0.5 -
                (ab_prev * (1 - ab_cur) / ab_cur)**0.5) * eps
if simple_var:
    third_term = (1 - ab_cur / ab_prev)**0.5 * noise
else:
    third_term = var**0.5 * noise
x = first_term + second_term + third_term

这样，下一刻的x就算完了。反复执行循环即可得到最终的结果。

实验

写完了DDIM采样后，我们可以编写一个随机生成图片的函数。由于DDPM和DDIM的接口非常相似，我们可以用同一套代码实现DDPM或DDIM的采样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def sample_imgs(ddpm,
                net,
                output_path,
                img_shape,
                n_sample=64,
                device='cuda',
                simple_var=True,
                to_bgr=False,
                **kwargs):
    if img_shape[1] >= 256:
        max_batch_size = 16
    elif img_shape[1] >= 128:
        max_batch_size = 64
    else:
        max_batch_size = 256

    net = net.to(device)
    net = net.eval()

    index = 0
    with torch.no_grad():
        while n_sample > 0:
            if n_sample >= max_batch_size:
                batch_size = max_batch_size
            else:
                batch_size = n_sample
            n_sample -= batch_size
            shape = (batch_size, *img_shape)
            imgs = ddpm.sample_backward(shape,
                                        net,
                                        device=device,
                                        simple_var=simple_var,
                                        **kwargs).detach().cpu()
            imgs = (imgs + 1) / 2 * 255
            imgs = imgs.clamp(0, 255).to(torch.uint8)

            img_list = einops.rearrange(imgs, 'n c h w -> n h w c').numpy()
            output_dir = os.path.splitext(output_path)[0]
            os.makedirs(output_dir, exist_ok=True)
            for i, img in enumerate(img_list):
                if to_bgr:
                    img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
                cv2.imwrite(f'{output_dir}/{i+index}.jpg', img)

            # First iteration
            if index == 0:
                imgs = einops.rearrange(imgs,
                                        '(b1 b2) c h w -> (b1 h) (b2 w) c',
                                        b1=int(batch_size**0.5))
                imgs = imgs.numpy()
                if to_bgr:
                    imgs = cv2.cvtColor(imgs, cv2.COLOR_RGB2BGR)
                cv2.imwrite(output_path, imgs)

            index += batch_size

为了生成大量图片以计算FID，在这个函数中我加入了很多和batch有关的处理。剔除这些处理代码以及图像存储后处理代码，和采样有关的核心代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def sample_imgs(ddpm,
                net,
                output_path,
                img_shape,
                n_sample=64,
                device='cuda',
                simple_var=True,
                to_bgr=False,
                **kwargs):

    net = net.to(device)
    net = net.eval()

    with torch.no_grad():
        shape = (n_sample, *img_shape)
        imgs = ddpm.sample_backward(shape,
                                    net,
                                    device=device,
                                    simple_var=simple_var,
                                    **kwargs).detach().cpu()

如果是用DDPM采样，把参数表里的那些参数填完就行了；如果是DDIM采样，则需要在kwargs里指定ddim_step和eta。

使用这个函数，我们可以进行不同ddim_step和不同eta下的64x64 CelebAHQ采样实验，以尝试复现DDIM论文的实验结果。

我们先准备好变量。

1
2
3
4
5
net = UNet(n_steps, img_shape, cfg['channels'], cfg['pe_dim'],
            cfg.get('with_attn', False), cfg.get('norm_type', 'ln'))
ddpm = DDPM(device, n_steps)
ddim = DDIM(device, n_steps)
net.load_state_dict(torch.load(model_path))

第一组实验是总时刻保持1000，使用$\hat{\sigma}_t$（标准DDPM）和$\eta=0$（标准DDIM）的实验。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
sample_imgs(ddpm,
            net,
            'work_dirs/diffusion_ddpm_sigma_hat.jpg',
            img_shape,
            device=device,
            to_bgr=to_bgr)
sample_imgs(ddim,
            net,
            'work_dirs/diffusion_ddpm_eta_0.jpg',
            img_shape,
            device=device,
            to_bgr=to_bgr,
            ddim_step=1000,
            simple_var=False,
            eta=0)

把参数n_samples改成30000，就可以生成30000张图像，以和30000张图像的CelebAHQ之间算FID指标。由于总时刻1000的采样速度非常非常慢，建议使用dist_sample.py并行采样。

算FID指标时，可以使用torch fidelity库。使用pip即可安装此库。

1
pip install torch-fidelity

之后就可以使用命令fidelity来算指标了。假设我们把降采样过的CelebAHQ存储在data/celebA/celeba_hq_64，把我们生成的30000张图片存在work_dirs/diffusion_ddpm_sigma_hat，就可以用下面的命令算FID指标。

1
fidelity --gpu 0 --fid --input1 work_dirs/diffusion_ddpm_sigma_hat --input2 data/celebA/celeba_hq_64

整体来看，我的模型比论文差一点，总的FID会高一点。各个配置下的对比结果也稍有出入。在第一组实验中，使用$\hat{\sigma}_t$时，我的FID是13.68；使用$\eta=0$时，我的FID是13.09。而论文中用$\hat{\sigma}_t$时的FID比$\eta=0$时更低。

我们还可以做第二组实验，测试ddim_step=20（我设置的默认步数）时使用$\eta=0$, $\eta=1$, $\hat{\sigma}_t$的生成效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
sample_imgs(ddim,
            net,
            'work_dirs/diffusion_ddim_sigma_hat.jpg',
            img_shape,
            device=device,
            simple_var=True,
            to_bgr=to_bgr)
sample_imgs(ddim,
            net,
            'work_dirs/diffusion_ddim_eta_1.jpg',
            img_shape,
            device=device,
            simple_var=False,
            eta=1,
            to_bgr=to_bgr)
sample_imgs(ddim,
            net,
            'work_dirs/diffusion_ddim_eta_0.jpg',
            img_shape,
            device=device,
            simple_var=False,
            eta=0,
            to_bgr=to_bgr)

我的FID结果是：

1
2
3
eta=0: 17.80
eta=1: 24.00
sigma hat: 213.16

这里得到的实验结果和论文一致。减少采样迭代次数后，生成质量略有降低。同采样步数下，eta=0最优。使用sigma hat的结果会有非常多的噪声，差得完全不能看。

综合上面两个实验来看，不管什么情况下，使用eta=0，得到的结果都不会太差。

从生成速度上来看，在64x64 CelebAHQ上生成256张图片，ddim_step=20时只要3秒不到，而ddim_step=1000时要200秒。基本上是步数减少到几分之一就提速几倍。可见，DDIM加速采样对于扩散模型来说是必要的。

参考文献及学习提示

如果对DDIM公式推导及其他数学知识感兴趣，欢迎阅读苏剑林的文章：
https://spaces.ac.cn/archives/9181。

DDIM的论文为Denoising diffusion implicit models(https://arxiv.org/abs/2010.02502)。

我在本文使用的公式符号都基于DDPM论文，与上面两篇文章使用的符号不一样。比如DDIM论文里的$\alpha$在本文中是用$\bar{\alpha}$表示。

DDIM论文在介绍新均值公式时很不友好地在3.1节直接不加解释地给出了公式的形式，并在附录B中以先给结论再证明这种和逻辑思维完全反过来的方法介绍了公式的由来。建议去阅读苏剑林的文章，看看是怎么按正常的思考方式正向推导出DDIM公式。

除了在3.1节直接甩给你一个公式外，DDIM论文后面的地方都很好读懂。DDIM后面还介绍了一些比较有趣的内容，比如4.3节介绍了扩散模型和常微分方程的关系，它可以帮助我们理解为什么DDPM会设置$T=1000$这么长的加噪步数。5.3节中作者介绍了如何用DDIM在两幅图像间插值。

要回顾DDPM的知识，欢迎阅读我之前的文章：DDPM详解。