今年四月,北大和字节跳动在 Arxiv 上发表了论文 Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction,介绍了一种叫做 Visual Autoregressive Modeling (视觉自回归建模,VAR)的全新图像生成范式。这种自回归生成方法将高清图像用多尺度词元图像表示,并用下一尺度预测代替了此前常用的下一词元预测。在 ImageNet $256 \times 256$ 图像生成任务上,VAR 的表现超越了 DiT。我们组的同学第一时间看了这篇论文,大家都觉得这篇论文有不小的创新,但其方法能否完全代替扩散模型还有待验证。通常来说,这篇论文的关注度会逐渐降下去,但近期发生的两件大事将 VAR 论文的热度推向了空前的高度:论文一作的严重违纪行为招致字节跳动对其索赔 800 万元、论文被评选为 Neurips 2024 会议的最佳论文。借此机会,我决定认真研究一下这篇论文并把我的学习结果分享给大家。
在这篇博文中,我会先回顾与 VAR 密切相关的早期工作 VQVAE 和 VQGAN,再介绍论文的方法细节与实验结果,最后分享我对该工作的测试结果与原理探究。在读 VAR 论文时,我发现有个地方的设计存在缺陷。相关实验结果表明, VAR 论文并没有完整地分析出这套方法有效的原因。欢迎大家仔细阅读这一部分并提出自己的思考与见解。
论文链接:https://arxiv.org/abs/2404.02905
VQGAN 原理回顾
VAR 算是 VQGAN 工作的改进版,而 VQGAN 又是 VQVAE 工作的改进版。要了解 VAR 的背景知识,最直接的方法就是回顾 VQVAE 与 VQGAN 这两个经典工作。我们先从自回归这种生成范式开始聊起,再将目光移向图像自回归生成,最后复习 VQVAE, VQGAN, Transformer 的实现细节。
推荐大家阅读我之前写的相关博文:
轻松理解 VQ-VAE:首个提出 codebook 机制的生成模型
VQGAN 论文与源码解读:前Diffusion时代的高清图像生成模型
Attention Is All You Need (Transformer) 论文精读
图像自回归生成
自回归(Autoregressive)是一种直观易懂的序列生成范式:给定序列前 $n$ 个元素,模型输出第 $n+1$ 个元素;把新元素添加进输入序列,再次输出第 $n+2$ 个元素……。以下是文本自回归生成的一个示例:1
2
3
4(空) -> 今
今 -> 天
今天 -> 早
今天早 -> 上
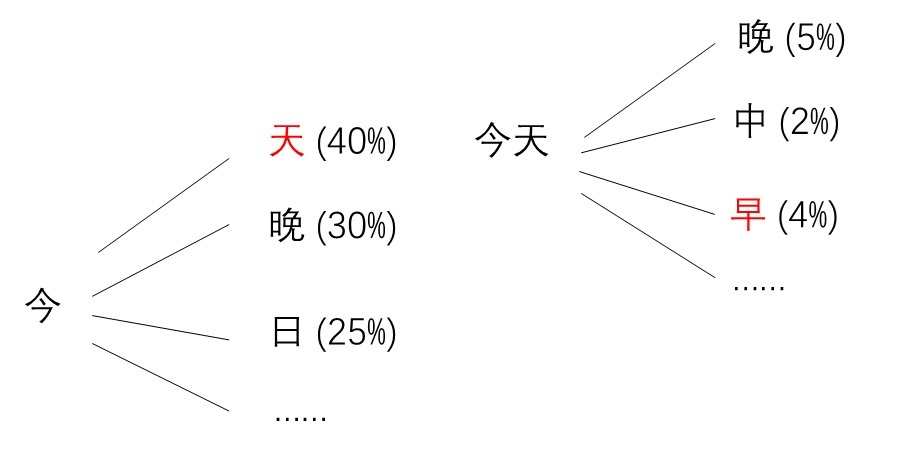
具体来说,模型的输出并不是下一个元素应该是什么,而是下一个元素可能是什么。也就是说,模型的输出是下一个元素的概率分布。通过不断对下一个元素采样,我们就能随机生成出丰富多样的句子。
自回归生成仅适用于有顺序的序列数据。为了用自回归生成图像,我们需要做两件事:1)把图像拆分成一个个元素;2)给各个元素标上先后顺序。为此,最简单的做法是将图像拆成像素,并从左到右,从上到下地给图像生成像素。比如下图是经典自回归图像生成模型 PixelCNN 的示意图。假设图像有 $3 \times 3$ 个像素,并按顺序从左上到右下标号。在生成第 $5$ 个像素时,模型只能利用已经生成好的前 $4$ 个像素的信息。模型的输出是一个概率分布,表示灰度值大小分别取 0, 1, ..., 255 的概率。
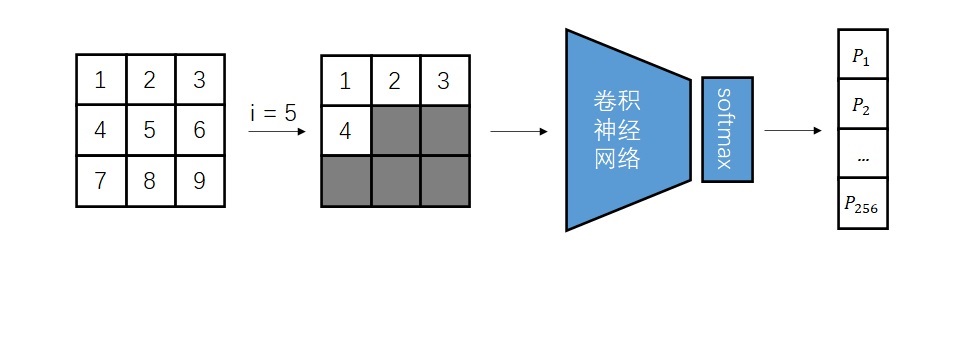
顺带一提,建模概率分布的方法有很多种,这里我们使用的分布被称为类别分布(categorical distribution)。这种方法的好处是形式简洁,可以用简单的算法采样,缺点是元素的取值必须是离散的。比如虽然图像的灰度值理论上可以取 0~1 中间的任何实数(假设灰度值被归一化了),但我们用上图所示的 PixelCNN 时,只能表示 0, 1/255, 2/255, ..., 1 这 256 种灰度值,而不能表示更加精确的值。
VQVAE
PixelCNN 虽然能做图像生成,但它的效率太慢了:由于像素是逐个生成的,要生成几个像素,就要运行几次神经网络。能不能加速生成过程呢?如果要生成的图像更小一点就好了。
为了加速 PixelCNN,借助图像压缩网络,VQVAE 工作提出了一种两阶段的图像生成方法:先生成压缩图像,再用图像压缩网络将其复原成真实图像。由于压缩图像的像素数较少,而复原压缩图像的速度又很快,整套生成方法的速度快了很多。
以下是一个 VQVAE 的生成示例。根据 PixelCNN 输出的类别分布,我们可以采样出一些由离散值构成的压缩图像。这些离散值就和 NLP 里的文字一样,每一种值都有一种特殊的含义。我们可以认为离散值表示原始图像中一大块像素的颜色。借助图像压缩网络的解码器,我们可以把压缩图像复原成清晰的原始图像。
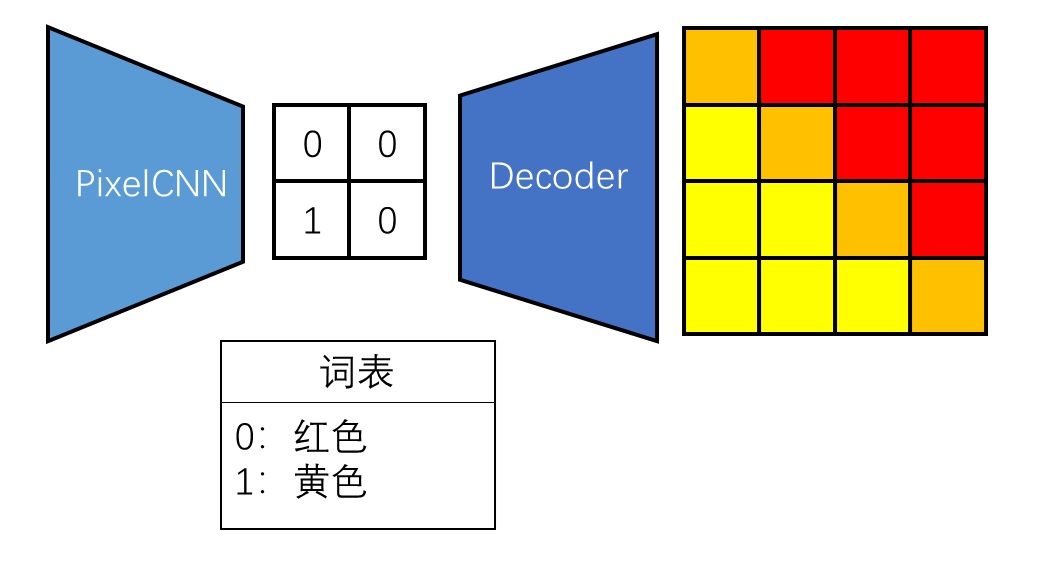
VQVAE 的训练顺序和生成顺序相反。我们先训练一个图像压缩网络。这种由编码器和解码器组成的图像压缩网络被称为自编码器,压缩出来的图像被称为隐图像(latent image)。训练好了自编码器后,我们再把训练集的所有图像都转成隐图像,让 PixelCNN 学习生成隐图像。比较有趣的是,训练 PixelCNN 时,只会用到编码器;而生成时,只会用到解码器。
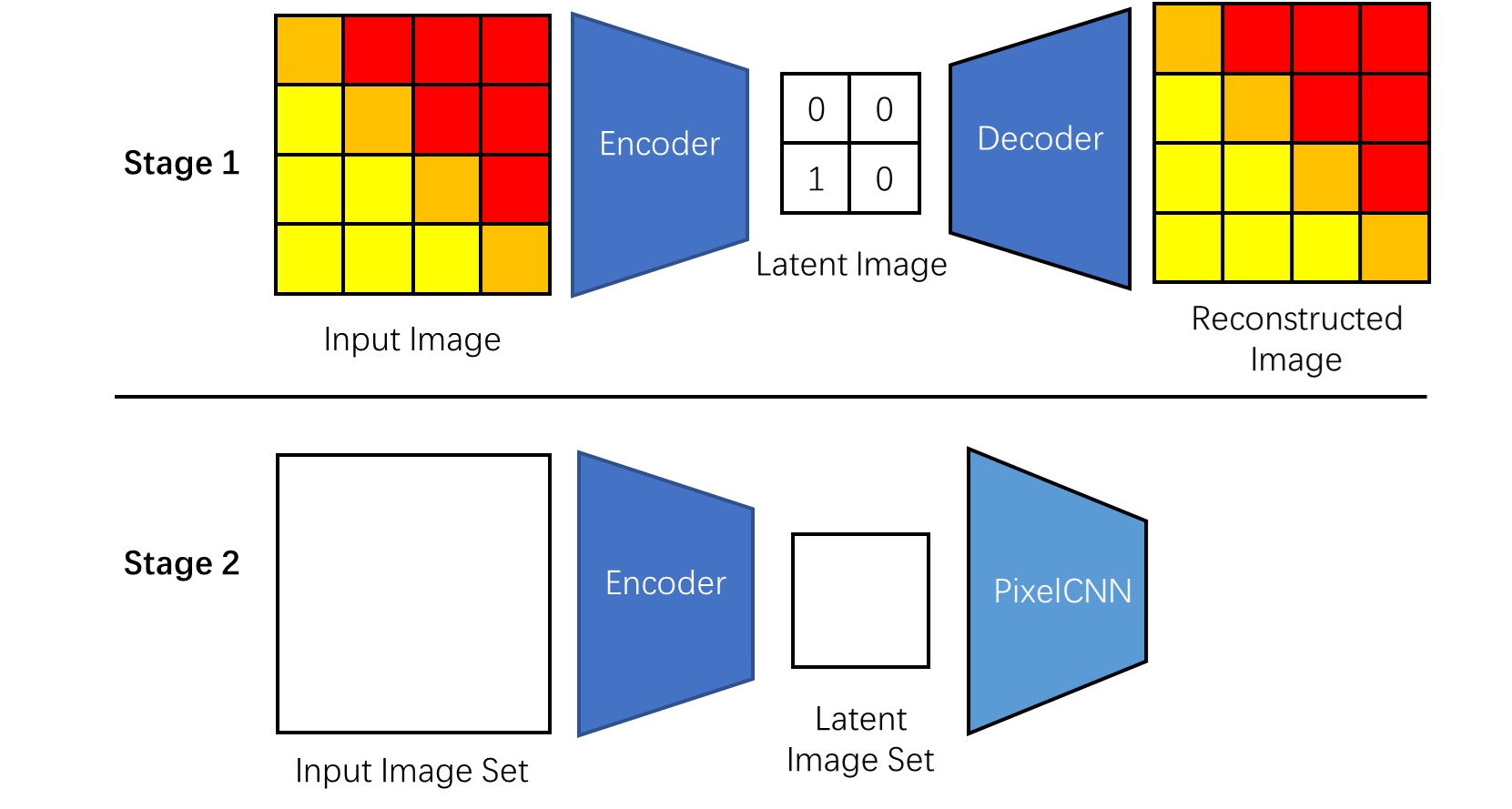
在上述讨论中,我们略过了一个实现细节:该怎么让网络以离散值为输入或输出呢?输入离散值倒还好办,在 NLP 中,我们用嵌入层把离散的词语变成连续向量,这里的做法同理。可怎么让网络输出离散值呢?这里就要用到向量离散化(vector quantization, VQ)操作了。
离散化操作我们都很熟悉,将小数四舍五入至整数就是一种最常见的离散化。四舍五入,本质上是让一个小数变成最近的整数。同理,对于向量而言,假设我们已经准备好了一些向量(对应前面的「整数」),那么向量离散化就表示把输入的任意向量变成最近的已知向量。这里的「最近」指的是欧几里得距离。
具体示例如下所示。编码器可以输出一个由任意向量构成的二维特征。通过查找嵌入层里的最近邻,这些任意的向量会被转换成整数,表示最近邻的索引。索引可以被认为是 NLP 里的词元 (token),这样编码器输出特征就被转换成了词元构成的隐图像。而在将隐图像输入进解码器时,我们把嵌入层当成一张表格,利用隐图像里的索引,以查表的形式将隐图像转换成由嵌入构成的特征。准确来说,这个把图像压缩成离散隐图像的自编码器才被叫做 “VQVAE”,但有时我们也会用 VQVAE 代表整套两阶段生成方法。
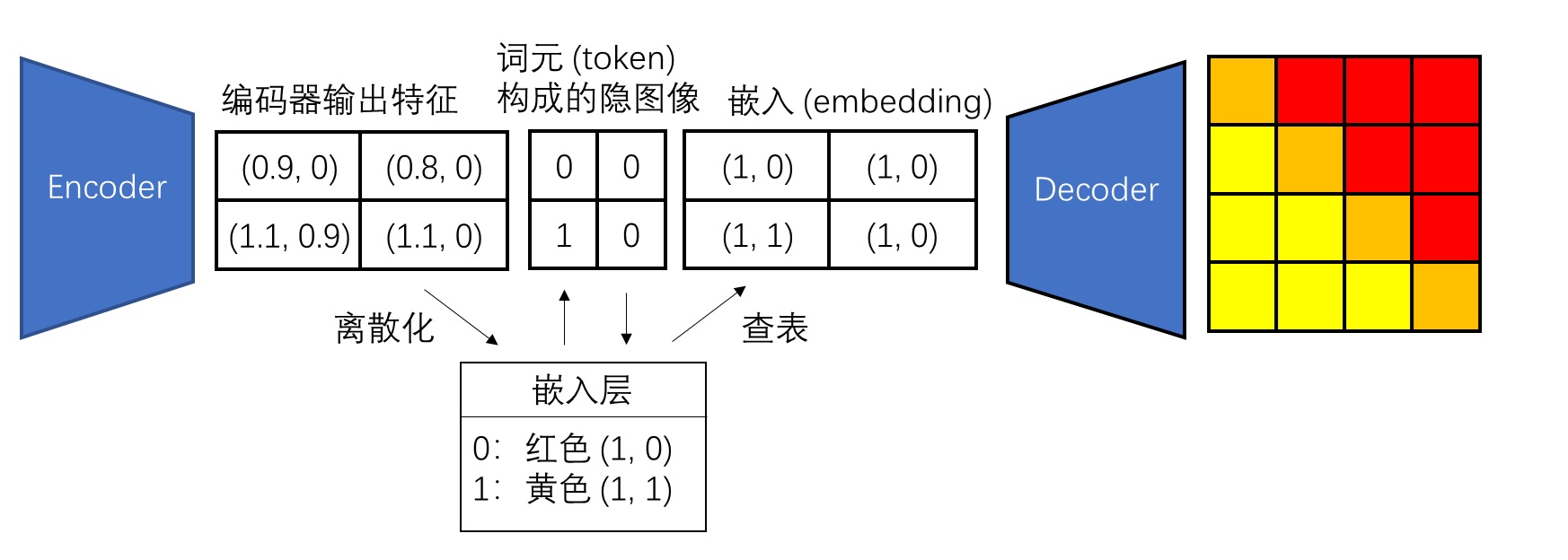
上图中的「编码器输出特征」、「词元」、「嵌入」在不同论文里有不同的叫法,且一般作者都只会用数学符号来称呼它们。这里我们用了 VAR 论文的叫法。
嵌入层的具体学习过程我们不在此展开,对这块知识不熟悉的读者可以去仔细学习 VQVAE 论文。
VQGAN
VQVAE 的效果并不理想,这是因为它的压缩网络和生成网络都不够强大。为此,VQGAN 工作同时改进了 VQVAE 的两个网络。
- VQGAN 工作将离散自编码器 VQVAE 换成了 VQGAN。在 VQVAE 的基础上,VQGAN 在训练时添加了感知误差和 GAN 误差,极大提升了自编码器的重建效果。
- VQGAN 工作还把生成模型从 PixelCNN 换成了 Transformer。
Transformer
Transformer 是目前最主流的主干网络。相比其他网络架构,Transformer 的最大特点是序列里的元素仅通过注意力操作进行信息交互。因此,为了兼容文本自回归生成任务,最早的 Transformer 使用了两个特殊设计:
- 由于注意力操作不能反映输入元素的顺序,词元嵌入在输入进网络之前,会和蕴含了位置信息的位置编码相加。
- 自回归生成要求之前的词元不能看到之后的词元的信息。为了控制词元间的信息传播,Transformer 给自注意力操作加上了掩码。
VQGAN 用了完全相同的设计,把图像词元当成文本词元用 Transformer 来生成。
从词元预测到尺度预测
上述的传统图像自回归生成都是采用下一个词元预测策略:
- 将图像用自编码器拆成离散词元。
- 从左到右、从上到下按顺序逐个生成词元。
尽管通过自编码器的压缩,要生成的词元数已经大大减少,但一个个去生成词元还是太慢了。为了改进这一点,VAR 提出了一种更快且更符合直觉的自回归生成策略:
- 将图像用自编码器拆成多尺度的离散词元。比如,原来一张隐图像的大小是 $16 \times 16$,现在我们用一系列尺度为 $1 \times 1, 2 \times 2, …, 16 \times 16$ 的由词元构成的图像来表示一张隐图像。
- 从最小的词元图像开始,从小到大按尺度生成词元图像。
在这种策略下,我们要同时修改自编码器和生成模型。我们来看一下 VAR 是怎么做的。
多尺度残差离散自编码器
先来看自编码的修改。现在词元图像不是一张图像,而是多张不同尺度的图像。由于词元图像的定义发生了改变,编码器特征和嵌入的定义也要发生改变,如下图所示。
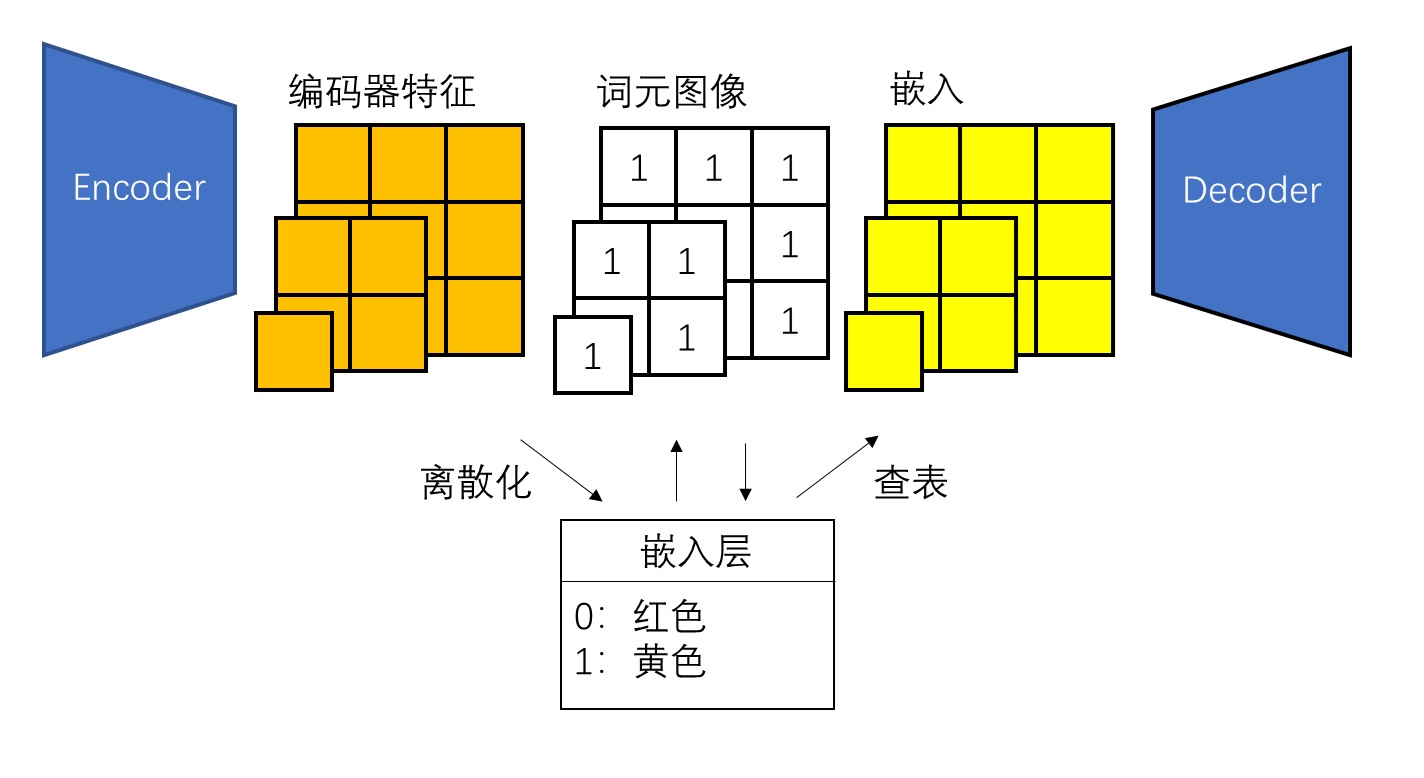
向量离散化部分我们可以沿用 VQVAE 的做法。现在新的问题来了:编码器的输出和解码器的输入都只是一张图像。该怎么把多尺度的图像组合成一张图像呢?
最简单的做法是完全不修改编码器和解码器,还是让它们输入输出最大尺度的图片。只有在中间的向量离散化/查表部分,我们才把这些图片下采样。
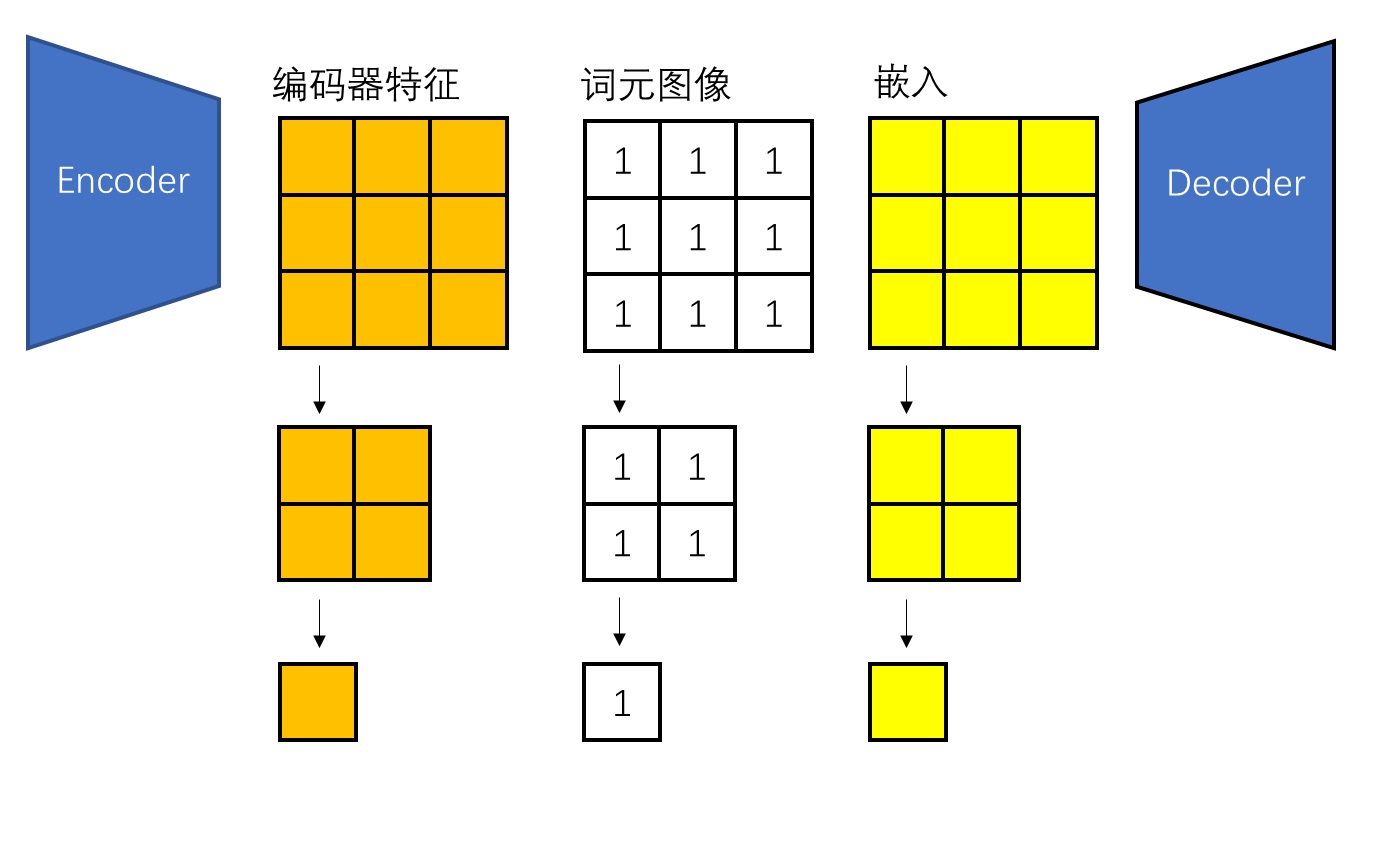
VAR 用了一种更加高级的做法:用残差金字塔来表示这些隐空间特征。我们先来回顾一下拉普拉斯金字塔这一经典图像处理算法。我们知道,图像每次下采样的时候,都会损失一些信息。既然如此,我们可以将一张高分辨率的图像表示为一张低分辨率的图像及其在各个分辨率下采样后的信息损失。如下图所示,最右侧的一列表示拉普拉斯金字塔的输出。

在计算拉普拉斯金字塔时,我们不断下采样图像,并计算当前尺度的图像和下一尺度的复原图像(通过上采样复原)的残差。这样,通过不断上采样最低尺度的图像并加上每一层的残差,我们最终就能精准复原出高分辨率的原图像。
现在,我们想把类似的金字塔算法应用到编码器特征上。该怎么把最大尺度的编码器特征拆解成不同尺度的图像的累加呢?
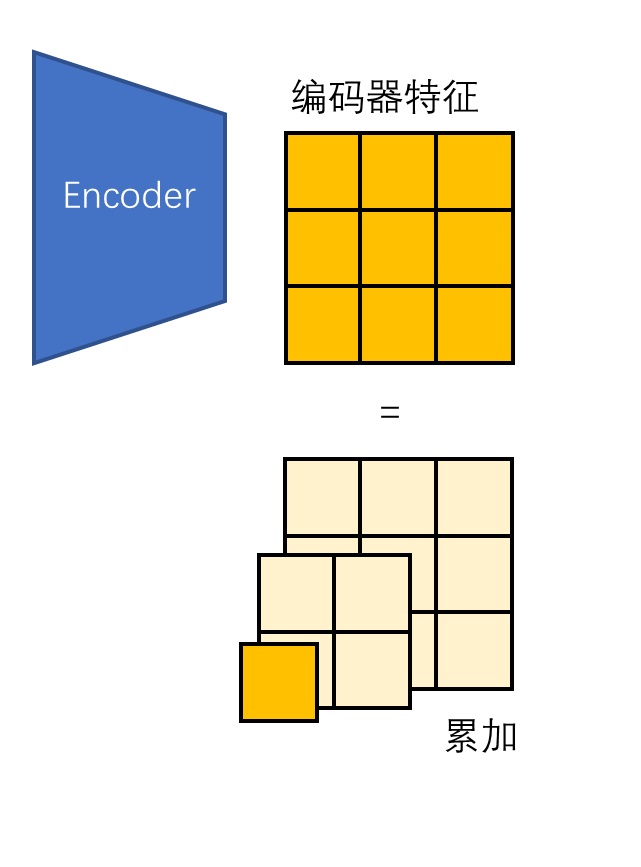
在计算拉普拉斯金字塔时,本质上我们用到了两类操作:退化和复原。对于图像而言,退化就是下采样,复原就是上采样。那么,对于编码器输出的隐空间特征,我们也需要定义类似的退化和复原操作。比较巧妙的是,VAR 并没有简单地把退化和复原定义为下采样和上采样,而是参考 Autoregressive Image Generation using Residual Quantization 这篇论文,将向量离散化引入的误差也算入金字塔算法的退化内。也就是说,我们现在的目标不是让编码器特征金字塔的累加和编码器特征相等,而是想办法让嵌入金字塔的累加和编码器特征尽可能相似,如下图所示。
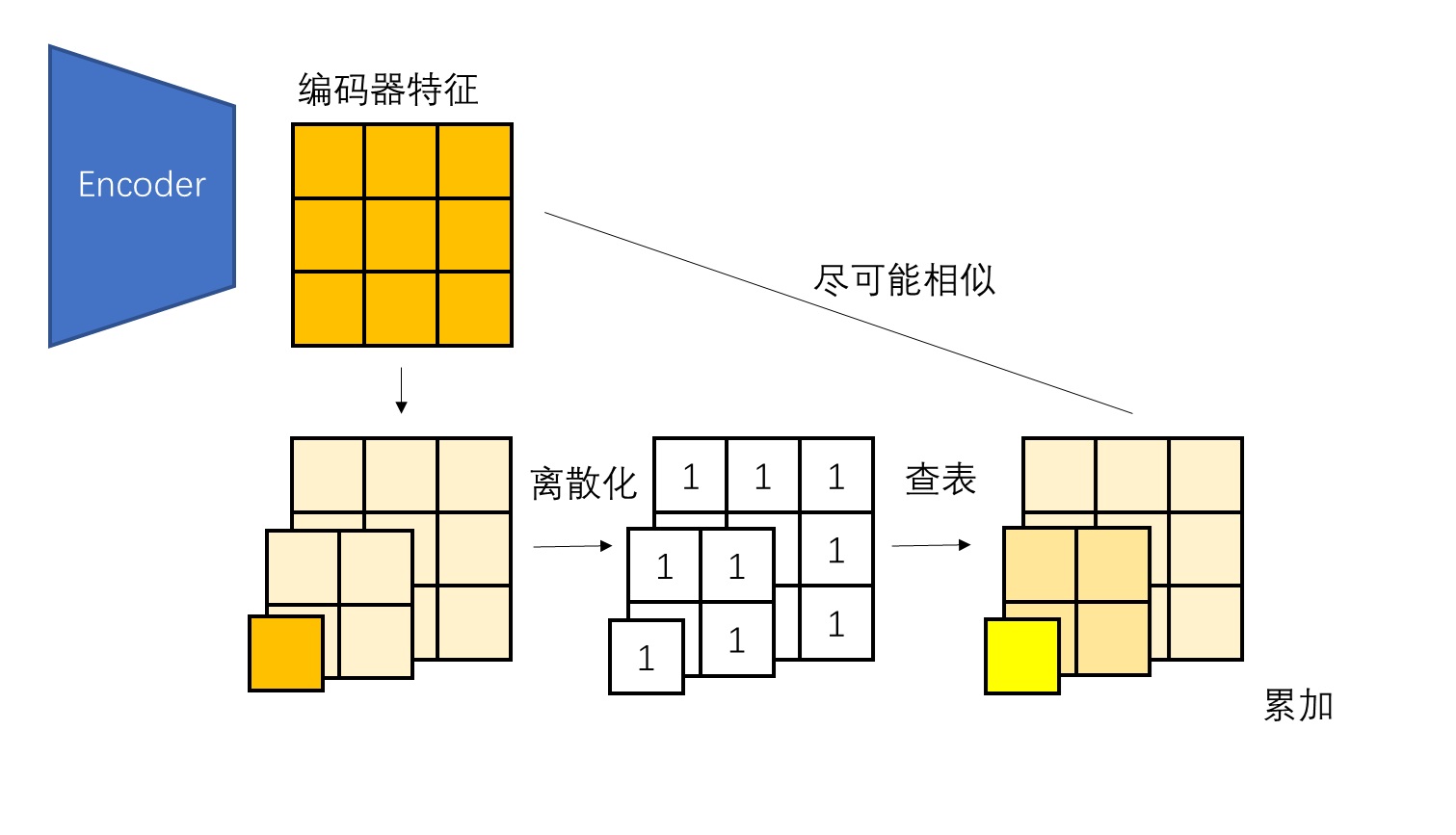
基于这一目标,我们可以把退化定义为下采样加上离散化、查表,复原定义成上采样加一个可学习的卷积。我们来看看在这种新定义下,原来 VQVAE 的向量离散化操作和查表操作应该怎么做。
先看新的多尺度向量离散化操作。这个操作的输入是编码器特征,输出是一系列多尺度词元图像。算法从最低尺度开始执行,每个循环输出当前尺度的词元图像,并将残差特征作为下一个循环的输入特征。
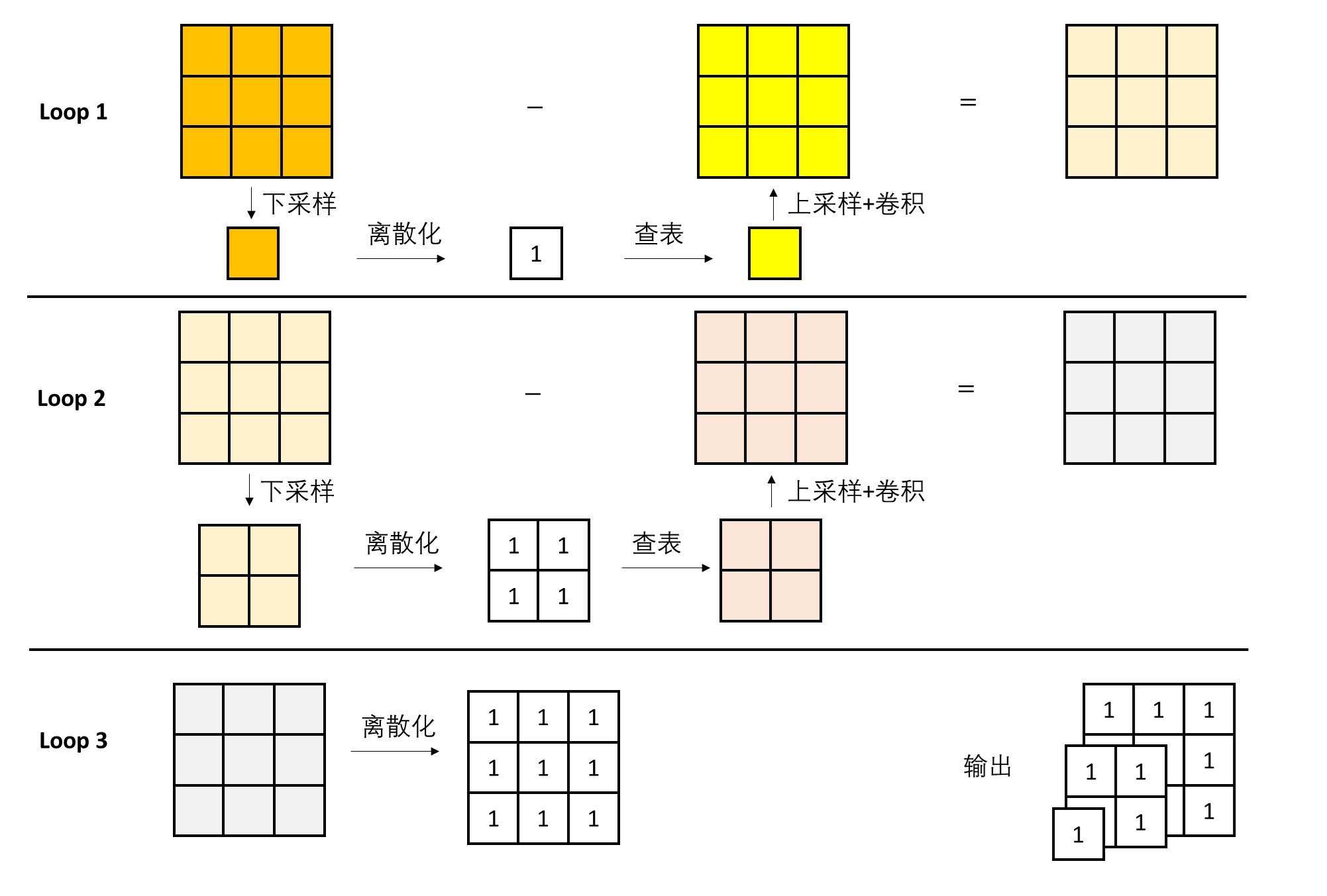
对于多尺度查表操作,输入是多尺度词元图像,输出是一张最大尺度的隐空间特征,它将成为自编码器的解码器的输入。在这步操作中,我们只需要分别对各个尺度的词元图像做查表和复原(上采样+卷积),再把各尺度的输出加起来,就能得到一个和编码器特征差不多的特征。注意,为了方便理解,这几张示意图都省略了部分实现细节,且一些数值不是十分严谨。比如在查表时,我们可以让不同尺度的词元共享一个嵌入层,也可以分别指定嵌入层。
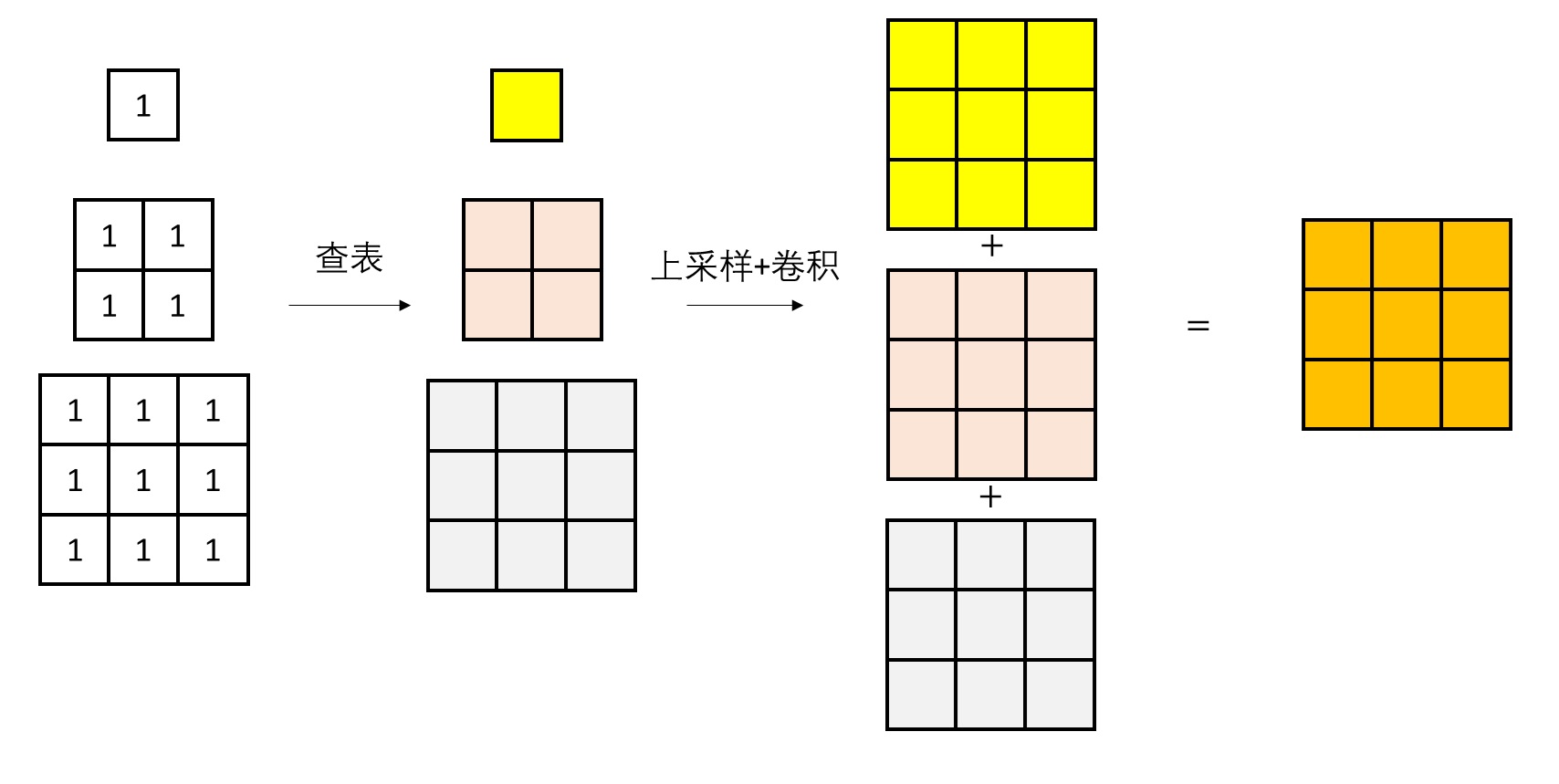
总结一下这一小节。为了实现尺度自回归生成,我们需要把图像编码成多尺度的词元图像。VAR 采用了一种多尺度残差离散化操作:将编码器特征拆解成最小尺度的特征以及不同尺度的残差特征,并对不同尺度的特征分别做向量离散化。这种做法不仅能高效地将特征拆解成多个尺度,还有一个额外的好处:原来 VQVAE 仅对最大尺度的特征做向量离散化,离散化后的误差会很大;而 VAR 把向量离散化引入的误差分散到多尺度离散化中,巧妙地降低了离散化的误差,提升了 VQVAE 的重建精度。
下一尺度自回归生成
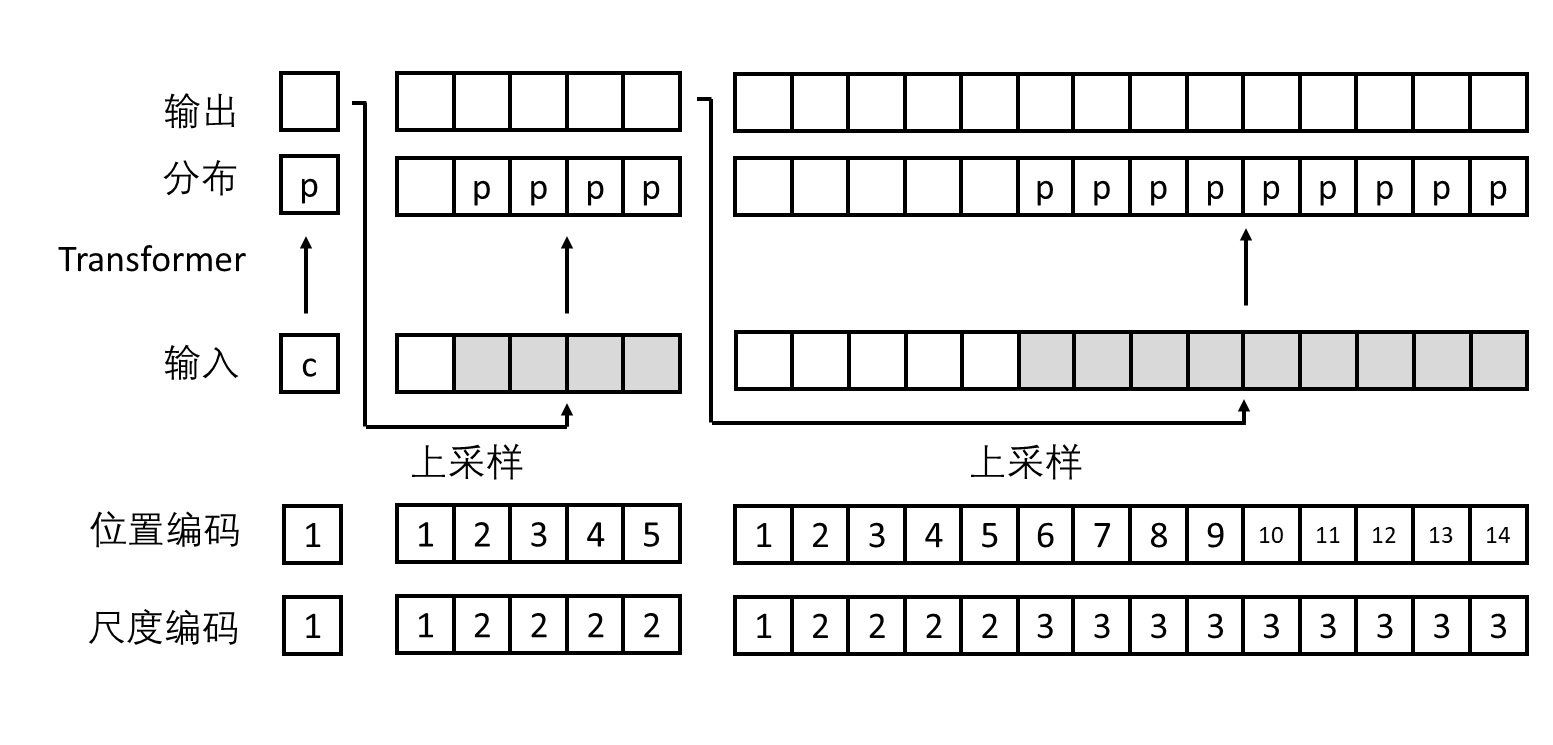
把图像压缩成多尺度词元图像后,剩下的事就很简单了。我们只需要把所有词元拆开,拼成一维词元序列,之后用 Transformer 在这样的序列上训练即可。由于现在模型的任务是下一尺度预测,模型会一次性输出同尺度各词元的概率分布,而不是仅仅输出下一个词元的。这样,尽管序列总长度变长了,模型的整体生成速度还是比以前快。同时,随着预测目标的变更,自注意力的掩码也变了。现在同尺度的词元之间可以互相交换信息,只是前一尺度的词元看不到后面的词元。以下是一个 $3 \times 3$ 词元图像在下一词元和下一尺度预测任务下的注意力掩码示意图及生成过程示意图。
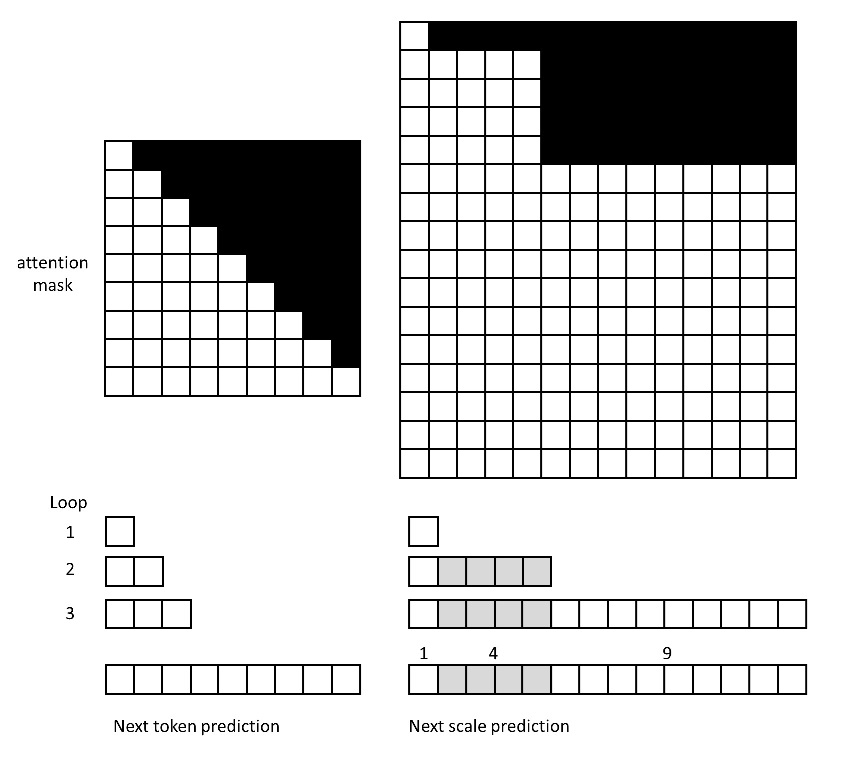
除此之外,VAR 的 Transformer 还做了一些其他修改:1)除了给每个词元加上一维位置编码外,同一尺度的词元还会加上同一个表示尺度序号的位置编码。所有位置编码都是可学习的,而不是预定义的正弦位置编码。2)Transformer 与解码器的共用嵌入层。另外,在生成新一层时,为了复用已经生成好的图像的信息,新一层的初始嵌入是通过对上一层的生成结果 bicubic 上采样得到的。
该 Transformer 的其他设计都与 VQGAN 相同。比如,Transformer 采用了 decoder-only 的结构。为了添加 ImageNet 类别约束,第一层的输入是一个表示类别的特殊词元。训练时用的误差函数是交叉熵函数。
ImageNet 图像生成定量实验
VAR 的方法部分我们看得差不多了,现在来简单看一下实验部分。论文宣称 VAR 在图像生成实验和参数扩增实验上都取得了不错的成果。特别地,VAR 的拟合能力胜过了 DiT,生成速度是 DiT 的 45 倍以上。我们就主要看一下 VAR 在 ImageNet $256 \times 256$ 图像生成上的实验结果。以下是论文中的表格。我同时还附上了何恺明团队的 MAR 工作(Autoregressive Image Generation without Vector Quantization)的实验结果。
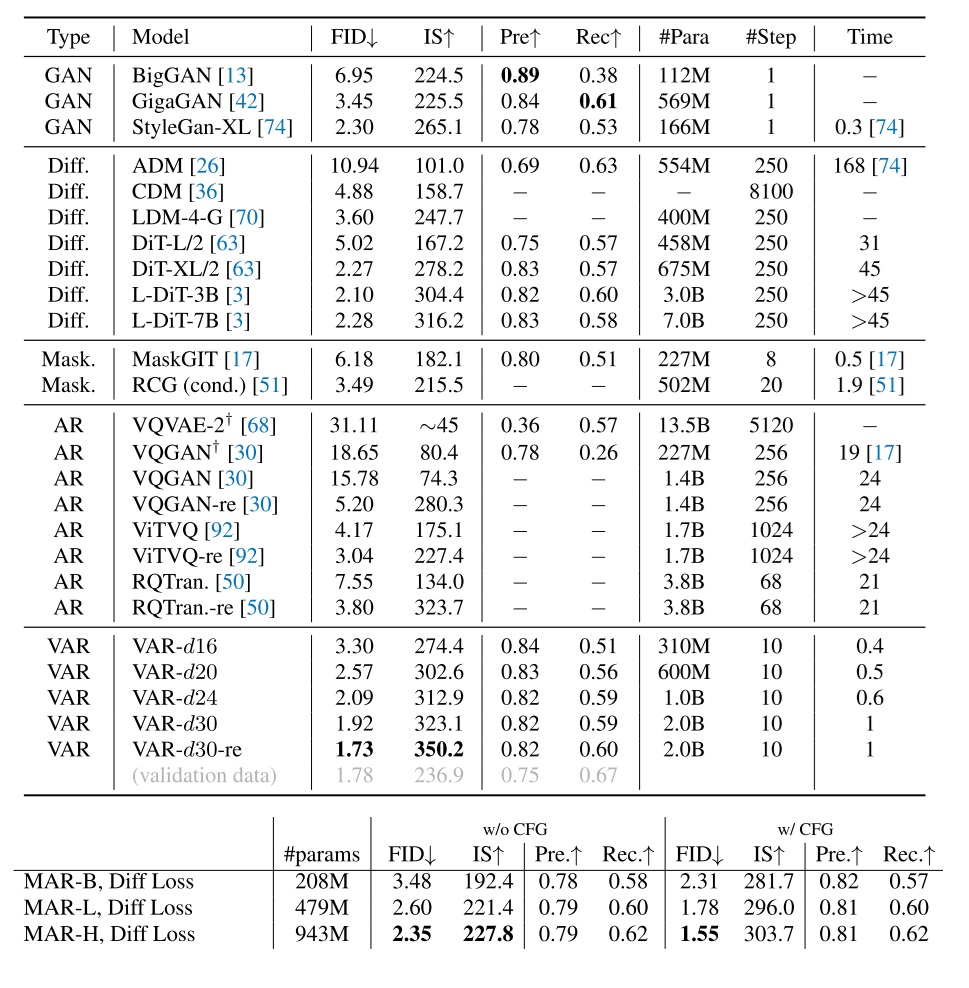
先比一下 DiT 和 VAR。先看速度,不管是多大的模型,DiT 的速度都远远慢于 VAR。再看以 FID 为代表的图像拟合指标。VAR 在参数量为 600M 左右时并没有 DiT 效果好。但继续增加参数量后,DiT 的 FID 没有变好的趋势,而 VAR 的 FID 一直在降。最终 VAR 的 FID 甚至超过了 ImageNet 的验证集,可以认为 FID 再低的也意义不大了。
再比一下 MAR 和 VAR。MAR 的刷指标能力更加恐怖,943M 的模型就能有 1.55 的 FID。但根据 MAR 论文,其速度是 DiT-XL 的 5 倍左右,也就是说 VAR 还是比 MAR 快,是 MAR 速度的 9 倍左右。
ImageNet 图像生成已经被各个模型刷到头了。FID 结果能说明 VAR 的拟合能力很强,最起码不逊于 DiT。但在更有挑战性的文生图任务上,VAR 的效果还有待验证。另外,虽然刷指标的时候 DiT 用了 250 步采样,但实际用起来的时候一般就是采样 20 步。如果算上蒸馏的话,采样步数能缩小到 4 步。加上这些加速技巧的话,VAR 不见得会比 DiT 快。
VAR 各尺度生成结果
看完了论文的主要内容,我来分享一下我对 VAR 的一些理论分析与实验结果。
先看一下随机采样结果。我用的是最大的 d=30 的 VAR 模型。在官方采样脚本的默认配置下,两个随机种子 (0, 15) 的输出如下所示。用到的图像类别为火山、灯塔、老鹰、喷泉,每个类别的图各生成了两张。图像的生成速度很快,一秒就生成了全部 8 张图片。

我们还可以观察每个尺度的生成结束后解码出的临时图片。和我们预估得一样,图像是按从粗到精的顺序逐渐生成的。

为了进一步探究每一个尺度负责生成哪些图像成分,我们可以做如下的实验:从某个尺度开始,随机更换新的随机数生成器。这样,每张动图里不变的部分就是前几个尺度生成好的内容;不断在变的部分就是后几个尺度负责的内容。可以看出,从第三个尺度开始,图像的内容就基本固定下来了,也就是说结构信息是在前两个尺度里生成的。越往后,图像的细节越固定。

这个结果还挺令人惊讶的:难道 $2 \times 2$ 这么小的特征图就已经决定了图像的整体内容?让我们来仔细探究这一点。
有缺陷的单尺度生成
不知道大家在学习 VAR 的采样算法时候有没有感到不对劲:在生成同一个尺度的词元图像时,每个词元是独立地在一个概率分布里采样。
而根据作者在论文里的说法,VAR 的尺度自回归是一种新的自回归概率模型:
其中,$r_k$ 表示从小到大第 $k$ 个尺度的词元图像,共 $K$ 个尺度。同一个尺度的词元图像 $r_k$ 的每个词元的分布是并行生成的。这也就是说,VAR 的这种训练(用交叉熵误差)和采样方式是认为每张词元图像的概率等于所有词元的概率的乘积,词元的分布之间是独立的:
其中,$r_k^i$ 表示第 $k$ 个尺度的第 $i$ 个词元,$I_k$ 为第 $k$ 个尺度的词元总数。我觉得上面这个等式是不成立的,哪怕有之前尺度的信息作为约束,同一尺度的每个词元的概率分布之间不会是互不相关的。且随着 $I_k$ 的增大,上面这个式子的误差会越来越大。
词元之间的采样互相独立,理论上会导致图像出现不连贯的地方。比如,假设一个图像词元表示 $16 \times 16$ 个像素,那么每隔 16 个像素图像就会出现「断层」。但是,为什么 VAR 的输出结果那么正常呢?仔细分析 VAR 的生成算法,我们可以发现有两项设计提升了图像的连续性:
- VAR 的自编码器使用了向量离散化操作。这个操作会让解码器的输入总是合理的,解码器也总是会输出连贯的图像。
- 在生成一个新尺度的图像时,模型输入会被初始化成之前尺度的图像的 bicubic 上采样。bicubic 采样保证了词元嵌入之间的连续性。

此外,为了进一步缓解独立采样带来的负面影响,VAR 在生成完第二或第三个尺度后就已经把图像的整体内容确定下来了,后面的生成只是略微影响图像细节而已(因为随着词元数量变多,独立采样的误差越大)。这个结论已经在前文的可视化结果中验证了。为了证明只有前几个尺度是重要的,我做了一个大胆的实验:用 Transformer 生成完前两个尺度的词元后,后续所有词元都随机生成。如下图所示,我展示了固定前两个尺度的输出后,多个随机种子下的生成结果。结果显示,如果前两个尺度的词元生成得比较好,后面词元无论采样得多乱,都不怎么会影响最终的图像质量。

根据这些实验结果,我认为 VAR 真正有效的原因并不能用「下一尺度预测这种全新生成范式更好」这样粗浅的话来概括。VAR 中最核心的组件可能是其多尺度残差离散自编码器。这个编码器至少做到了以下几件事:
- 使用向量离散化确保解码器的输入总是合理的。
- 使用多尺度残差设计,且下一尺度的残差图像不仅记录了因下采样而导致的信息损失,还记录了因向量离散化带来的精度损失。相比简单的、人类能够理解的拉普拉斯金字塔,这种可学习的多尺度拆分方法或许更加合理。
- 使用 bicubic 对低尺度词元图上采样。这步固定的操作让生成的图像总是连续的。
当然,这几件事是互相耦合的。不进行更深入的实验的话,我们难以解耦出 VAR 中最有效的设计。
多尺度生成其实并不是什么新奇的思想。之前 StyleGAN 和 Cascaded Diffusion 都用了类似的策略。然而,VAR 做了一个大胆的设计:同一尺度的不同词元在采样时是相互独立的。令人惊讶的是,这种在数学上不太合理的设计没怎么降低图像的质量。并且,得益于这一设计,VAR 能够并行地对同一尺度的词元采样,极大地提升了生成速度。
总结与评论
此前,以经典工作 VQGAN 为代表的图像自回归生成模型无论在速度上还是图像质量上都不尽如人意。究其原因,下一个图像词元预测的建模方式既不够合理,也拖慢了生成速度。为此,VAR 提出一种新式自回归策略:将词元图像拆分成多个尺度,通过下一尺度预测实现图像生成。为了兼容这一设计,VAR 对 VQGAN 的自编码器和 Transformer 都进行了修改:自编码器能够将图像编码成多尺度的残差词元图像,而 Transformer 同时输出同一尺度每个词元的独立分布。实验表明,VAR 在 ImageNet 图像生成指标上超越了以 DiT 为代表的扩散模型,且生成速度至少比 DiT 快 45 倍。另外,还有实验表明 VAR 符合扩增定律:增加参数量即可提升模型性能。
我个人认为,和其他前沿生成模型一样,VAR 在 ImageNet 上的表现已经满分了。它能否完成更困难的图像生成认为还有待验证。最近字节跳动发布了 VAR 的文生图版本:Infinity,但这个模型还没有开源。我们可以持续关注 VAR 的各个后续工作。VAR 的生成速度也没有比 DiT 快上那么多,通过减小采样步数,再加上模型蒸馏,DiT 不会比 VAR 慢。当然,VAR 或许也存在进一步加速的可能,只是相关研究暂时没有扩散模型那么多。
VAR 的数学模型是存在缺陷的:词元图的分布不应该等于词元间的独立分布的乘积。最起码论文里没有任何相关分析(用了类似做法的 MAR 论文也没有分析)。通过一些简单的生成实验,我们发现由于 VAR 在其他设计上提升了输出图像的连续性,哪怕同一尺度的词元间是独立采样,甚至是随机均匀采样,模型的输出质量也不会太差。我们需要通过更深入的实验来挖掘 VAR 的生效原理。
我觉得如果一个科研工作能够解释清楚 VAR 中哪些模块起到了最主要的作用,并取其精华,去其糟粕,提出一个更好的生成模型,那这会是一个很不错的工作。我觉得能够探索的方向有:
- VAR 的前几个尺度的词元图是最重要的。能不能用更好的方式,比如用扩散模型,来生成前几个尺度的图像,而更大尺度的词元图用一个比 Transformer 更高效的模型来生成。这样模型的质量和效率能进一步提升。
- VAR 还是用了 VQ 自编码器。无论怎么样,VQ 操作都会降低模型的重建质量。但另一方面,VQ 也能起到规范解码器输入的作用。究竟我们能不能把 VQ 自编码器换成精度更高的 VAE 呢?换了之后怎么设计多尺度编码呢?
以前我一直将 “quantization” 翻译成「离散化」,但经仔细学习后发现它与真正的离散化 “discretization” 存在区别。因此,以后我会采用「量化」这个更常见的翻译,尽管我认为这个翻译容易和「量化投资」里的「量化」混淆。