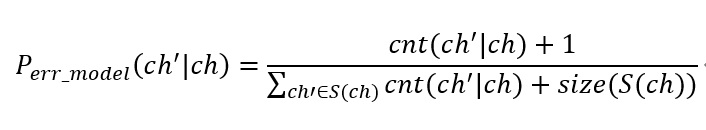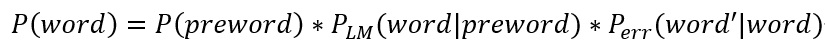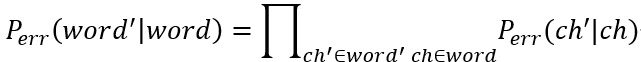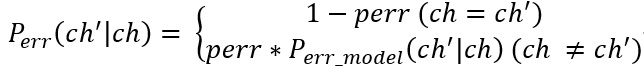和上一篇博文一样,这篇博文也是一个项目回顾与总结。
这个项目是我NLP的第二个大作业。在这个大作业中,老师要求做一个能完成某个功能(而不是做句法分析等预处理工作)的NLP程序。选题时可以从老师给定的题目中选,也可以自己找一个题目。当时我时间并不是很充足(感觉这学期我就没有在时间充裕的情况下写过项目),准备尽快把项目做完,因此决定从老师给的题目里挑一个来实现。一开始我挑了垃圾评论检测,因为老师明确指出,只要实现一篇论文的内容就行了。我去搜了那篇论文,却发现论文的数据集不是公开的,想获取数据集需要发邮件去申请,十分麻烦。我只好在剩下的题目中再找一个题目出来。排除掉了一些看上去不是那么实用的题目后,我选择了”汉语自动纠错系统“这个题目。在论文中,这个问题被称作”中文拼写检查(Chinese Spelling Check)”。
我很快搜索到了一篇非常好的综述博客[4]。根据博客中的介绍,我去读了几篇论文。比较幸运的是,这些论文中的算法对我来说非常简单,我很快就理解了算法的细节。比较了各种方法的实现难度并参考了综述博客对各种方法的比较结果后,我选择了[3]中的方法。一般来说,拼写检查问题可以分成两个部分:先对句子进行分词,再根据分词结果进行拼写检查。[3]的方法可以同时完成这个两个步骤,处理起来比较方便。
我很快实现了分词算法,并且按照评估标准评价了我的程序的表现。我本以为这个项目就这样结束了,但我对我程序极差的表现产生了一丝怀疑。我更仔细地阅读了一下论文,发现论文除了提出分词算法外,还提出了一种利用数据统计文字错误概率的方法。文章利用了谷歌1T的数据库来训练。我难以获取这个数据库,哪怕获取了电脑也存不下,哪怕存得下训练时间我也接受不了。考虑到这是大作业,老师不会只按结果给分,而更看重程序的原理、工作量。我于是决定用其他数据来代替论文中的1T数据,用论文中同样的方法来统计文字出错概率。
找数据又花费了我很多工夫。我需要一个包含文字错误的语料,标注可有可无。我找来找去,总算在Github上一个比较出名的中文语料库中找到了一个台湾论坛聊天语料。虽然数据量不够,但勉强可以在这个语料库上执行文章中的训练算法了。
在统计文字出错概率之前,需要先用一个分词语料库训练出一个语言模型。我用的是比较常用的北大人民日报语料。但是,所有的中文拼写检查都是基于繁体字的,这就出现了一个问题:语言模型仅用了简体语料,无法处理繁体字。我决定把人民日报语料转换成繁体。一开始我用word转换,一按简繁转换按钮程序就卡死了。我又去网上随便下了一个简繁转换程序。这个程序的转换速度倒是很快,但我发现转换结果有一些问题:一个简体字可能对应多个繁体字,比如简体”后“字有”(皇)后“,”後(面)“这两个对应的繁体字,而转换程序只能进行一对一的转换。最后我在Github上找了一个运用了NLP技术的简繁体转换程序,总算得到了一个能用的繁体语料库了。
至此,我总算解决了所有的问题,准备好了编程所需的所有资源。剩下的编程、写实验报告的工作就没什么值得讲的了。
这次项目对我来说意义很大。倒不是说我在这个项目中学到了多少NLP知识,或者说留下了一段比较有趣的工作过程。我在这次项目中,最大的收获是初步掌握了检索文献并了解一个领域前沿知识的能力。我第一次了解了什么是综述,虽然这篇综述放在博客上,并不是按照标准的论文格式写的。我第一次读懂论文并实现了论文的算法。我之前一直觉得论文都很高深,涉及的方法非常复杂。多亏这几篇论文算法相对来说比较简单,给了我读论文的自信。在这个项目之后,我还碰到了很多需要自主学习领域前沿知识的项目。得益于这次项目的经验,我能够快速搜索到一篇好的综述文章并开展学习,高效率地完成对相关领域前沿知识的了解。
以下项目介绍绝大多数内容摘自实验报告。
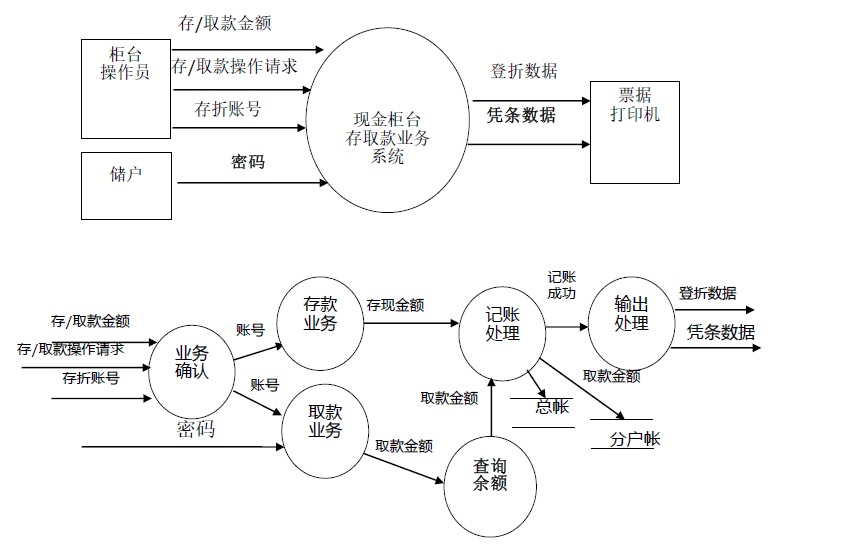
中文拼写检查器(基于图网格,C++实现)
Github链接
https://github.com/SingleZombie/Simple-Chinese-Spelling-Checker
任务定义
找出一个句子中出错字的位置。
把出错的字修改成正确的字。
实现思路
实现思路和参考论文[3]大致相同。
对一个句子同时进行分词和纠错。假设每个字都可能出错。列出每个字的混淆字,这样对于整个句子来说,就形成了一个图格。分词和纠错等于在图格上找一条权值最大的路径。在这个图格中,每个字都看成一个节点。如果相邻的几个字可能构成一个词(无论这些字是否来自混淆集),就把这个词当成一个节点。两个节点的之间的权值就是转移的概率。
节点间的概率来自两个部分,一部分是语言模型概率(判断分词是否正确),一部分是字会出错的概率(判断修改的是否正确)。
对于语言模型,使用大作业一的二元语言模型,即基于人民日报语料库构建的模型。每次可以查询前后两个词一起出现的概率。
对于字会出错的概率,使用互联网文本来训练模型。对文本的每句话进行分词(分词采用大作业一的算法),之后考虑任意连续的两个或三个词,试图用混淆集的字替换其中的一个字(混淆集来自汉语的同音字、近音字),看看这两个或三个词能否合并成一个词。如果能,则把改之前和改之后的字符串作为一个pair储存。这些pair表示候选错误串。
统计所有pair的情况。把每个pair的出错字符串的前面一个词看成一个向量(向量的维度是上一个字符串,向量该维度的值是上一个字符串出现次数)。同时,用同样方法统计pair的正确字符串的前一个向量,这个向量可以从语言模型中获得。对两个向量求cos值,该值可以表示两个向量的相似程度。若这个cos值大于一个人工设置的阈值,则认为错误串和正确串上文相同,这个串确实出错了。之后,把串中出错的字找到,统计一个字出错变成另一个字的个数。
有了一个字出错成另一个字的个数,就可以统计一个字出错成另一个字的概率。一个字符串出错变成另一个字符串的概率,就是每个字出错成对应字概率的乘积。
节点的转移权值由以上两部分概率相乘得到。
由于图格构成一个DAG,且已经拓扑排序好,可以用DP找最大权值的路。寻找每一个可能的词以构成节点时,在词典的字典树上查找以减少时间开销。找到最大权值的路后倒序得到每一个节点,出错纠错结果。
程序设计与实现
数据预处理
由于测试集是繁体,词典用的分词语料、汉语词典被转换成了繁体。
混淆集文本预处理模块如下所示:
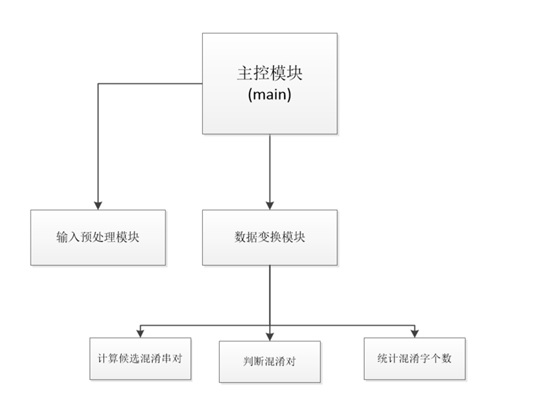
由于原始数据是json型的,数据先被提取出来,保存到txt文件里。(这一步程序里没有,只保留了最后的txt文件)
之后main函数调用outputConfusionPair进行候选串的获取。选取候选串的主要算法函数存在ConfusionTrainer.cpp文件中。其算法先对句子进行分词,再每次找相邻的两个、三个词,尝试从完整的混淆集(来自于汉语的同音、近音字)替换每个字,看这两个、三个词能否构成一个词典里的词。其具体算法和后面的替换算法类似,都是在词典的字典树上查找。最终这一步会输出三元组(上一个词,可能出错的词,正确的词)。
之后main函数调用calPotentialConfusionPair,LanguageModel统计上一步得到的三元组,根据出现次数计算输出出混淆对概率信息,这个信息文件里包含每一个混淆对的cos值,混淆对的出现次数。cos值是把对可能错误的词的上一个词的出现次数乘上语言模型中正确的词也是这个上一个词的出现次数再相加,最后除以正确的词上一个词的总个数,除以可能错误词上一个词的总个数。和向量求cos值方法相同。
最后confusionSet根据cos值和混淆对出现次数筛选掉一些不合法的混淆对(实现时cos值>=0.2,出现次数>=2),之后对合法的混淆对统计是哪个字出错了,最后得到一个字错误成另一个字的次数。根据一个字错成另一个字的个数,可以得到一个字错成另一个字的概率,具体公式是:
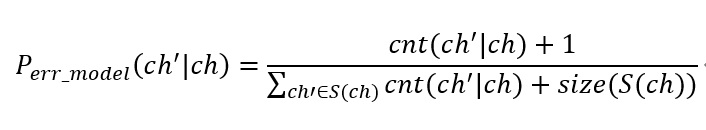
ch是正确字符,ch'是某一个被混淆的字符。S(ch)指字符ch的混淆集。由于样本数据较小,这里用了加1的数据平滑。
由于最后一步预处理很快,这一步的结果没有写进文件,在程序执行的时候才会处理。
程序执行
最终可执行程序的结构如下:
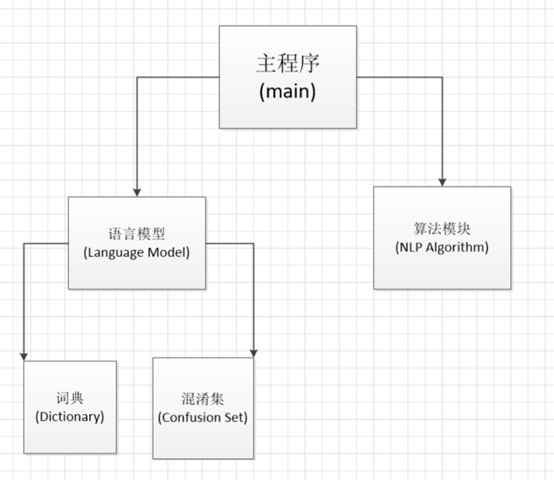
词典读入分词语料库,得到二元语法模型,同时所有词构成一个字典树。混淆集读入每个字所有可能的混淆字,以及每个混淆字的概率。语言模型综合二者的信息。算法模块提供了所有核心算法。主程序对整个程序的过程进行控制。
程序开始运行后,会先读入分词语料库,以及一个成语库,二者会插入进语言模型的词典。词典在内部建一棵字典树以维护所有词语,并统计相邻两个词出现概率。之后主程序会读入一个有概率的混淆集。最后调用Language Mode再调用NLPAlgorithm文件中的算法对测试集进行纠错并评价结果。
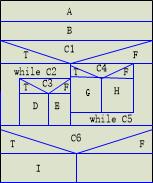
CSCAlgorithm.cpp包含本程序主要的纠错算法。主要函数的算法流程图如下:
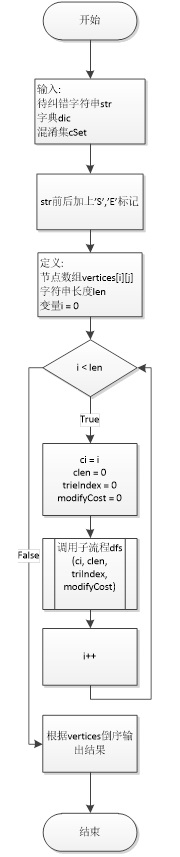
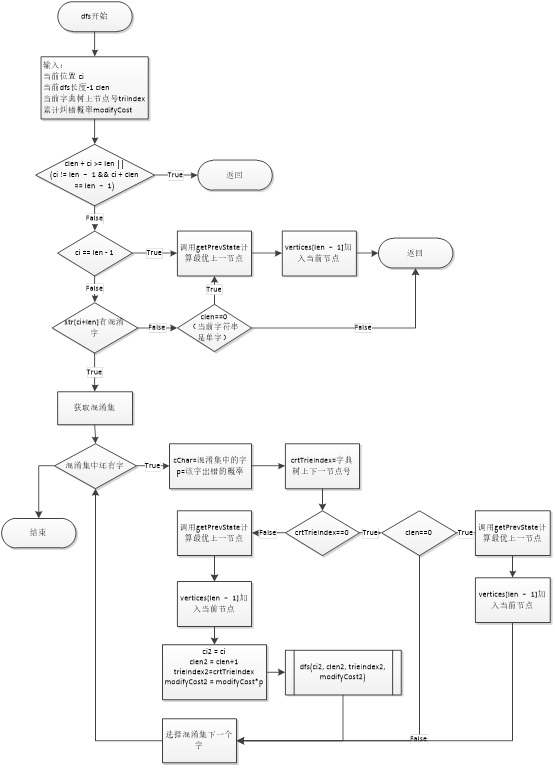
分词函数先定义了节点二维数组vertice[i][j],从字符串的每个位置开始进行DFS。DFS在递归过程中,会尝试替换每一个字符,并且在词典的字典树上移动。如果字典树上没这条路径,即当前节点号crtTrieIndex==0,就可以对DFS进行剪枝。通过DFS可以生成图网格中所有可能的词节点,并且得到每一节点的最大概率。通过最后一个节点可以反向遍历出结果字符串。
具体节点概率(准确来说是权值)计算公式如下:
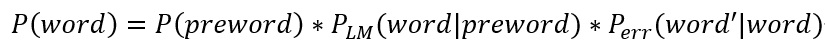
word指当前词,preword是上一词。$P_{LM}$是语言模型的概率,直接调用二元语法模型的函数就可以计算。$P_{err}$为出错概率,其公式为:
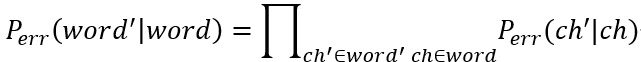
公式就是把出错词中每一个出错字的出错概率累乘。其中:
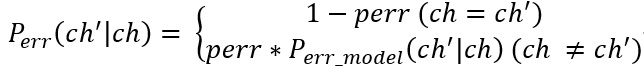
根据这个字是否出错,这个概率分两部分来计算。其中perr是一个超参数,表示某个字出错的概率。如果这个字确实是错的字,就去之前的错误模型里寻找概率。程序中这个值是CHARACTER_ERROR_P = 0.0003
程序结果
使用SIGHAN Bake-off 2013作为测试集。其中subtask1用于错误查找,subtask2用于错误纠正。根据测试集论文的描述,评价标准有以下几项:
错误查找:
FAR(错误识别率):没有笔误却被识别为有笔误的句子数/没有笔误的句子总数
DA(识别精准率):正确识别是否有笔误的句子数(不管有没有笔误)/句子总数
DP(识别准确率):识别有笔误的句子中正确的个数/识别有笔误的句子总数
DR(识别找回率):识别有笔误的句子中正确的个数/有笔误的句子总数
DF1(识别F1值):2 * DP * DR/ (DP + DR)
ELA(错误位置精准率):位置识别正确的句子(不管有没有笔误)/句子总数
ELP(错误位置准确率):正确识别出笔误所在位置的句子/识别有笔误的句子总数
ELR(错误位置召回率):正确识别出笔误所在位置的句子/有笔误的句子总数
ELF1(错误位置准确率):2 * ELP * ELR / (ELP+ELR)
错误纠正:
LA位置精确率:识别出笔误位置的句子/总的句子
CA修改精确率:修改正确的句子/句子总数
CP修改准确率:修改正确的句子/修改过的句子
我的结果:
FAR:16.5714% DA:70.0000% DP:50.0000% DR:38.6667% DF1:43.6090%
ELA:63.7000% ELP:22.8448% ELR:17.6667% ELF1:19.9248%
LA:16.3000% CA:15.2000% CP:37.1638%
使用的公共资源
语言模型
北大人民日报语料库
新华成语词典:https://github.com/pwxcoo/chinese-xinhua
混淆集
原始混淆集:SIGHAN2013 ConfusionSet
训练用互联网语料:https://github.com/zake7749/Gossiping-Chinese-Corpus
工具
简体繁体转换程序:https://github.com/hankcs/HanLP
测试集
SIGHAN2013 finalTest
程序实用说明
输入文件的格式必须是Unicode BE。
txt文件描述:
ChatData.txt 混淆集训练用的互联网原始文本
ChatDataConfusionSet.txt 互联网文本中提取的候选混淆对
ConfusionInfo.txt 候选混淆对筛选出的词对cos值和出现次数
FinalTest.txt SIGHAN测试集subtask2
FinalTest_Result.txt 程序跑出来的subtask2结果
FinalTest_Truth.txt subtask2正确答案
FinalTest_SubTask1.txt SIGHAN 测试集 subtask1
FinalTest_SubTask1_result.txt 程序跑出来的subtask1结果
FinalTest_SubTask1_Truth.txt subtask1正确答案
IdiomDictionary.txt 成语词典
SimilarPronunciation.txt SIGHAN原始混淆集
SimilarShape.txt SIGHAN原始混淆集
TrainDataCht.txt 北大分词语料
参考文献
[1]. Shih-Hung Wu, Chao-Lin Liu, and Lung-Hao Lee (2013). Chinese Spelling Check Evaluation at SIGHAN Bake-off 2013. Proceedings of the 7th SIGHAN Workshop on Chinese Language Processing (SIGHAN’13), Nagoya, Japan, 14 October, 2013, pp. 35-42.
[2]. Chao-Lin Liu, Min-Hua Lai, Kan-Wen Tien, Yi-Hsuan Chuang, Shih-Hung Wu, and Chia-Ying Lee. Visually and Phonologically similar characters in incorrect Chinese Words: analyses, Identification, and Applications. ACM Transactions on Asian Language Information Processing, 10(2), 10:1-39.
[3]. Hsieh Y M, Bai M H, Huang S L, et al. Correcting Chinese spelling errors with word lattice decoding[J]. ACM Transactions on Asian and Low-Resource Language Information Processing (TALLIP), 2015, 14(4): 18.
[4]. hqc888688.中文输入纠错任务整理[EB/OL].https://blog.csdn.net/hqc888688/article/details/74858126,2017-07-09.