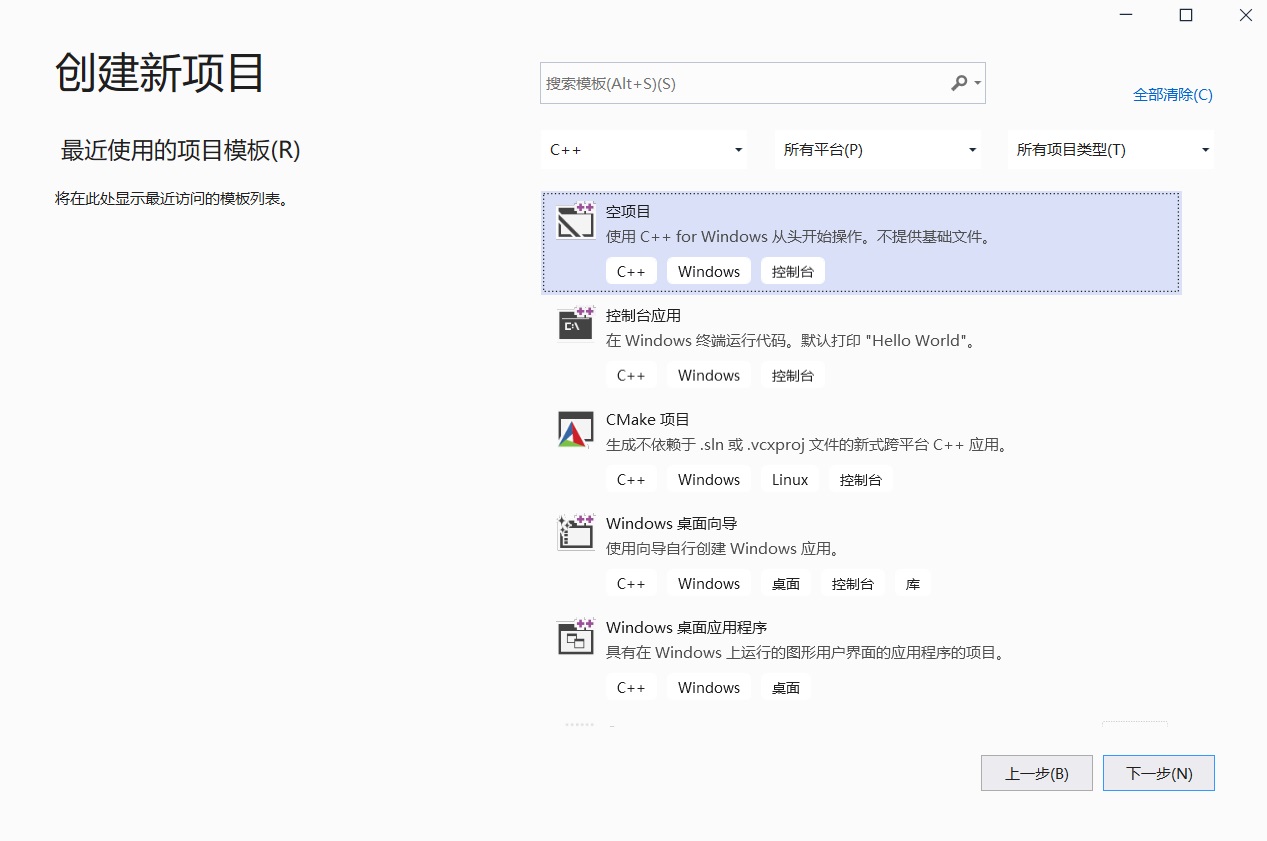
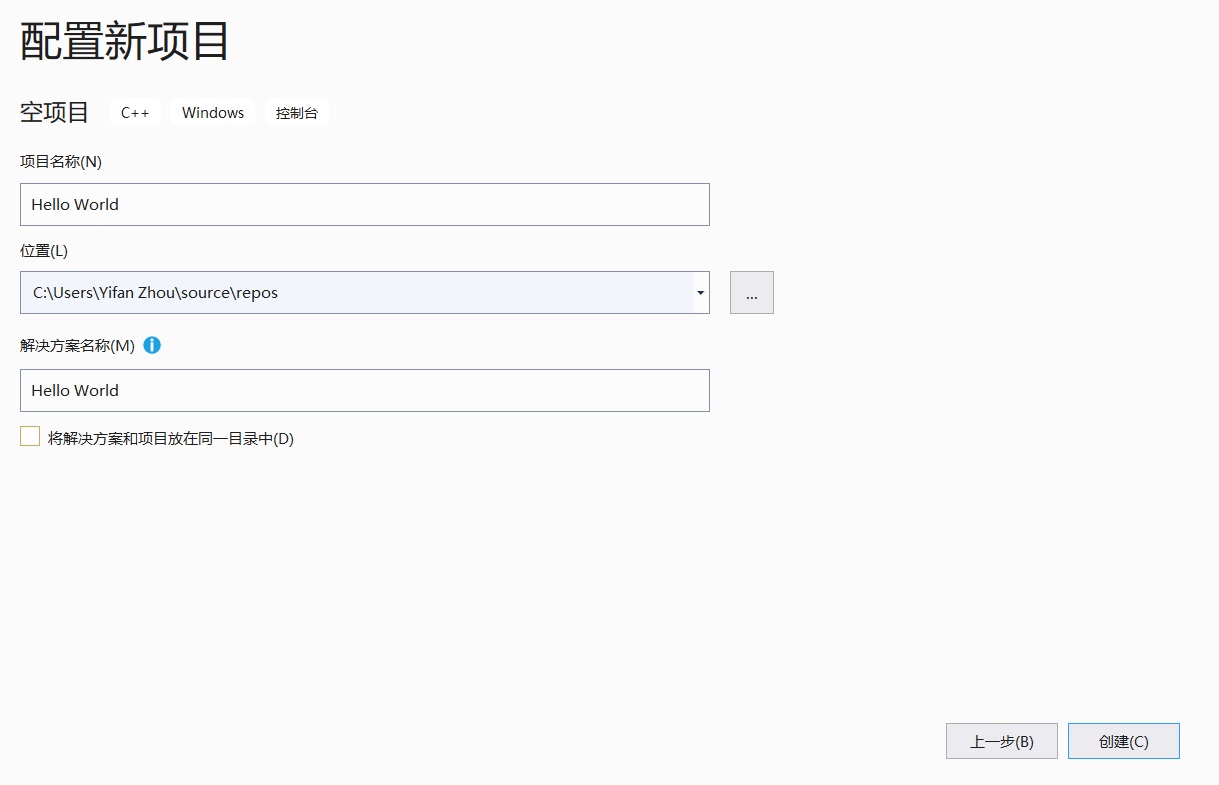
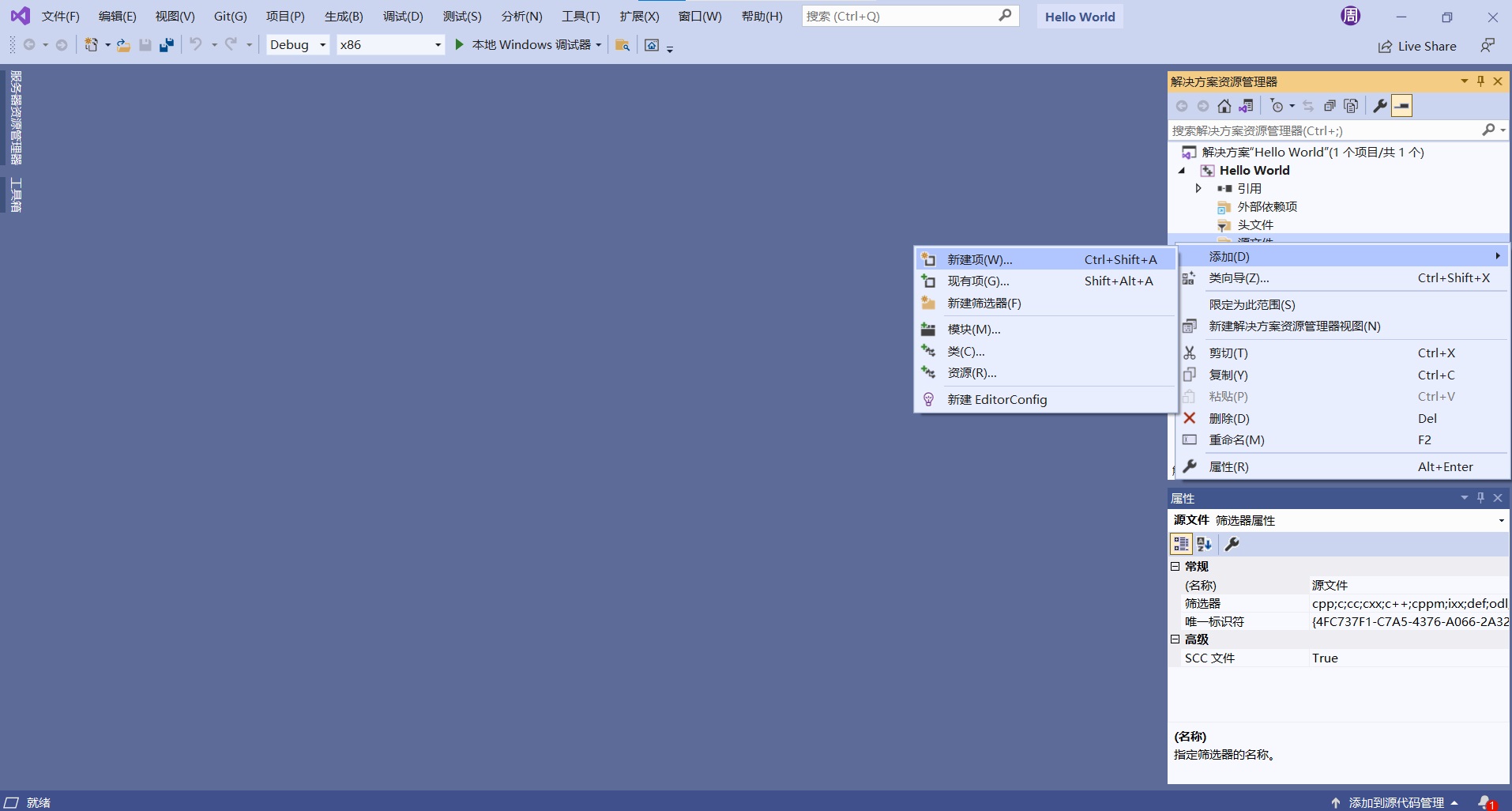
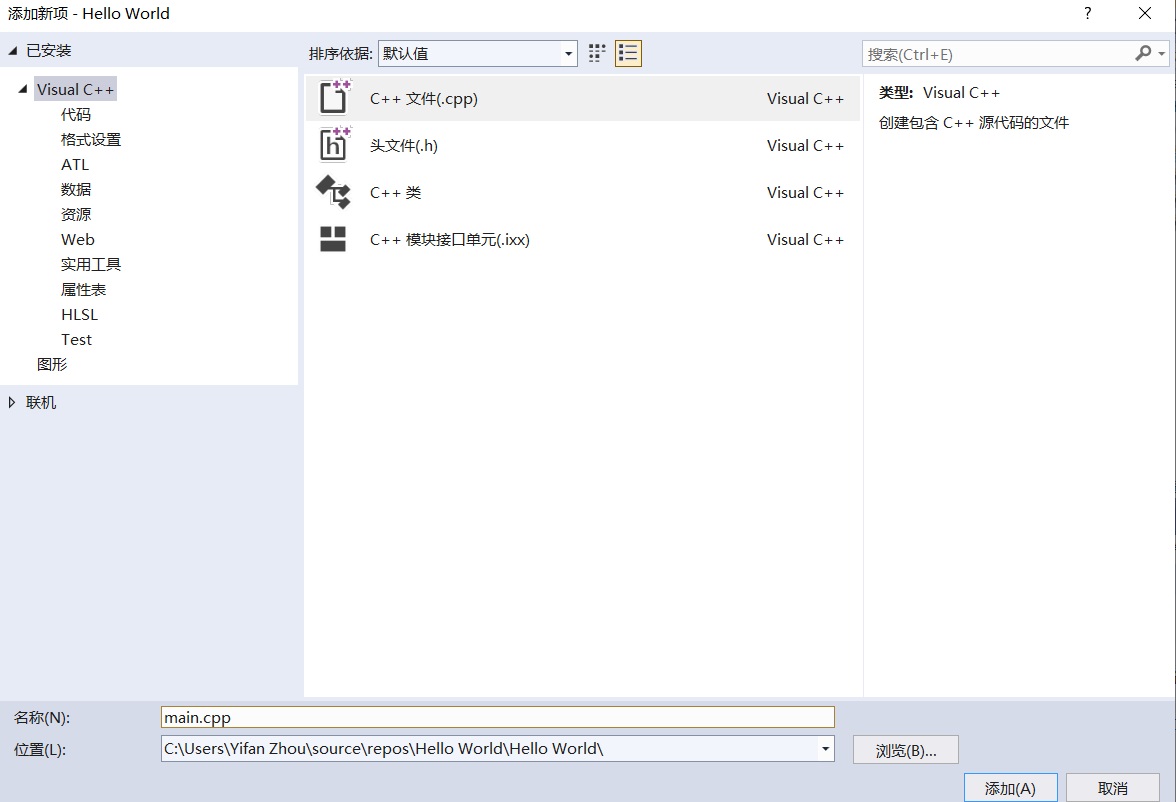
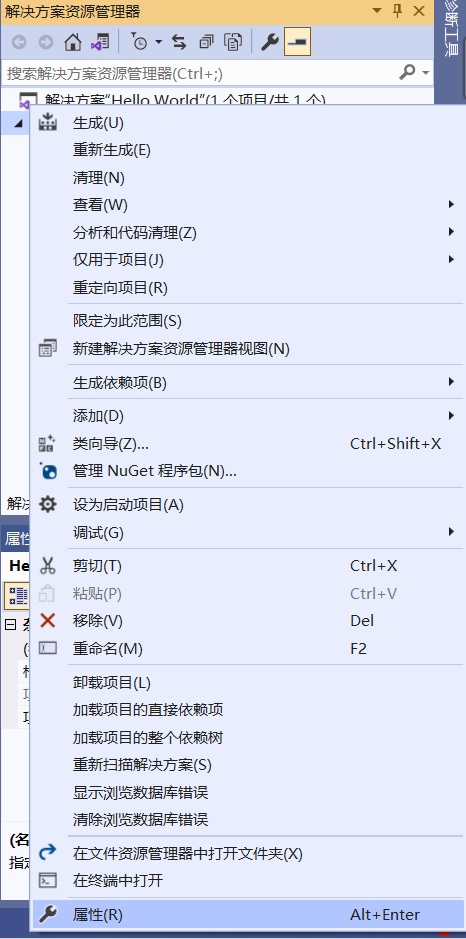
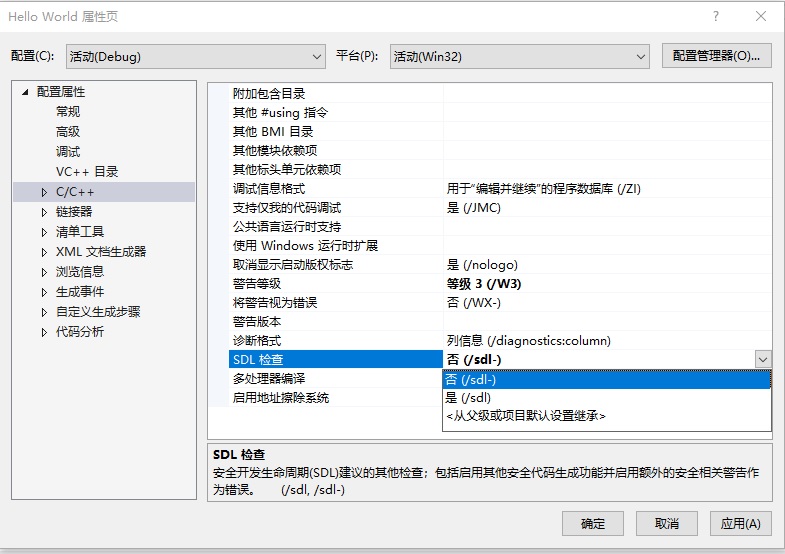
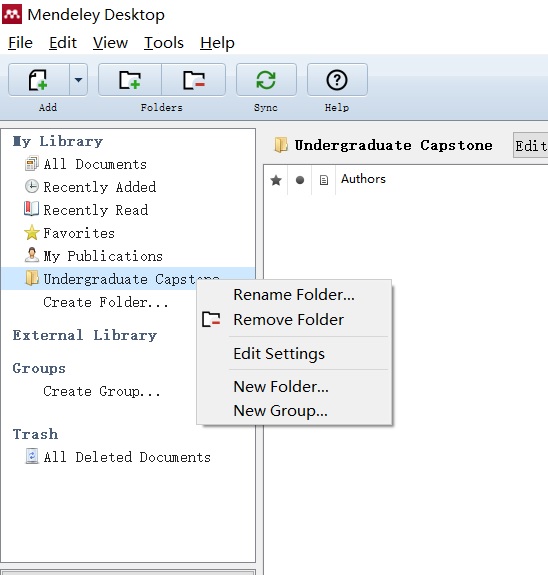
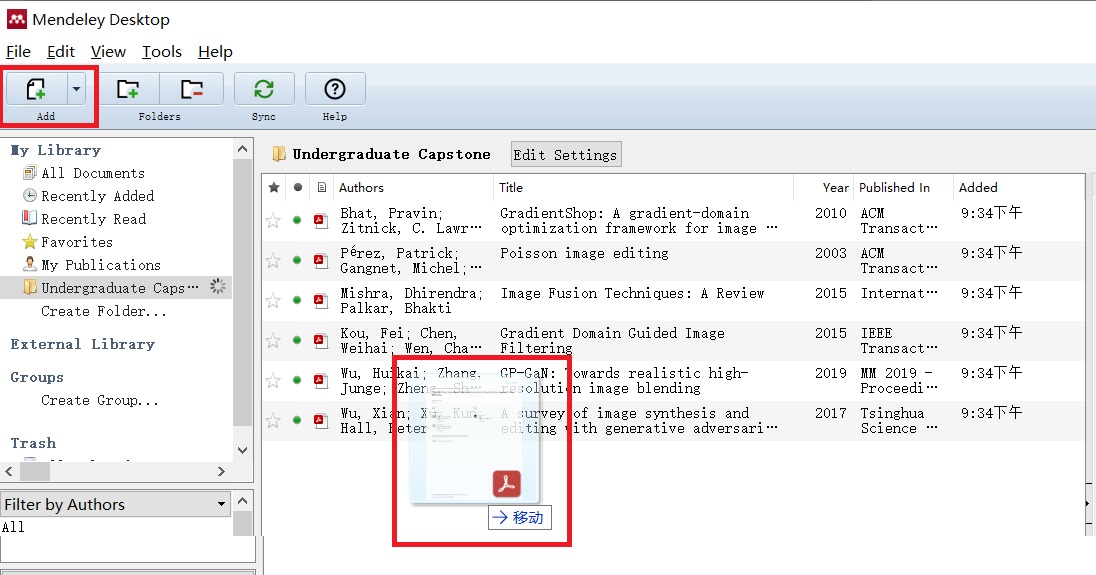
之前学了不少东西,今天以学习笔记的形式分享出来。学习笔记不适合作为入门的教程。
Git/Github使用方法学习笔记
从例子直观理解git
git是一个开源的分布式版本控制系统。如果你去网上搜git的定义,一定会搜到不少这样精确又令人看不懂的定义。今天,我准备根据我的笔记,来友好地介绍一下git相关的知识。
假设你要玩一个流程很长的RPG,你打了一天,打到了半夜。这个时候该做什么呢?没错,存档。不然下次就要从头开始玩游戏了。
除了继承之前的游戏进度,存档还有一个好处:如果你不小心输了,可以从上次存档的地方开始重新玩。甚至你玩着玩着发现进错了结局,可以从好早的档重新开始玩。存档,除了保存进度,还能记录下游戏发展向不同分支的关键节点。
现在再做一个很不现实的假设:你要玩一个无聊又冗长的RPG游戏,但是通关了之后你会得到一大笔钱。为此,你只开始关注能否尽快通关,而不去体验游戏的内容了。你在单位的电脑玩,在网吧的电脑玩,还在家里的电脑玩。你把所有好友都动员起来一起帮你玩游戏。但是每个人的进度不一样就没意义了。于是,你们想了个办法:大家玩完后,把存档放到网络上,下一个人就可以用最新的文档来了。
大家决定按贡献度分钱。同时,大家还想方便地交流每个人玩的具体情况,碰到了什么问题。于是,大家扩展了存档功能,不仅让存档保存游戏内容,还保存了每个人的保存时间、进行了多少游戏进度、想分享的游戏攻略等有意义的信息。
这就是git用法的一个形象的解释。在我的理解里,能够保存项目进度关键节点,并记录有意义的日志信息,就是一个版本控制,不同的人能在不同的设备上同步所有其他人的进度,就是分布式。源代码给你看,就叫开源。合起来呢,就变成了开源的分布式版本控制系统。
这个例子基本上是我自己想出来的,我在想这个例子的时候会主动思考git有哪些性质,这些性质与另一个通俗易懂的事情的哪些性质比较类似。通过这个过程,我反而加深了自己对git的理解。如果读者在学完git后,能够真正看懂这个例子,并且举出一个自己的例子,那就说明你基本理解了git。
这里推荐个比较有名的博客,上面有git的教程。我是跟着这篇博客上的教程入门git的。该教程举了个日志的例子(如下图)。该日志记录的内容,代表了git的大部分操作。可以暂且认为git就是一个自动生成这样格式的版本日志的程序。说得那么好听,git就是个自动记事本。

git的操作
一定要自己开一个项目去学习git,光看不动手很难学会
为了节约写作时间,让我能够写更多的学习笔记,最大化造福他人,我决定牺牲博文质量,偷懒地放上之前做的ppt。
Hello git!
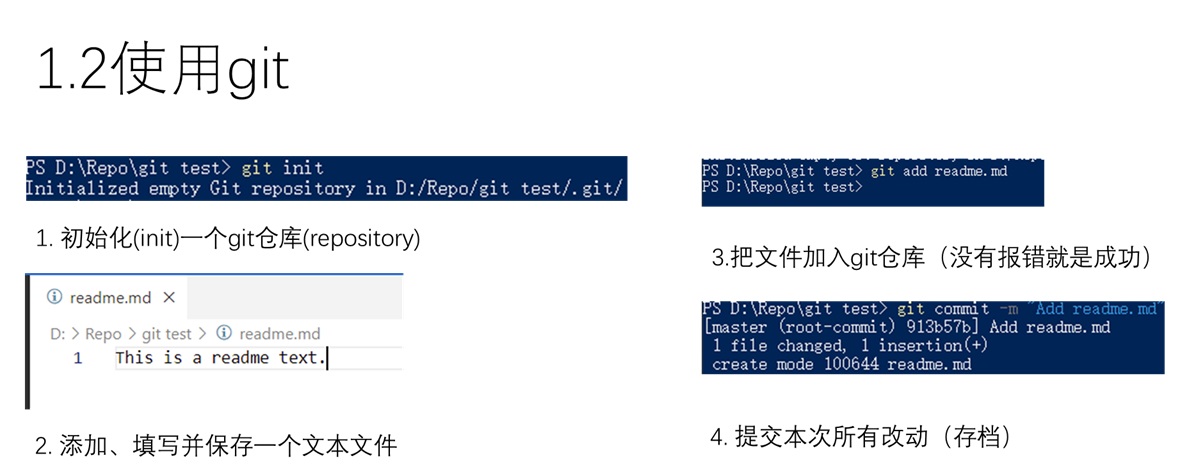
完成上图中的操作,你就可以像写完了一门新语言的hello world程序一样,说自己已经掌握git了。
这么说有点夸张,但也不假。上图介绍了一次完整的git使用流程。首先,需要使用git init初始化一个git仓库,呼叫git这个记录员来帮你管理版本,不然你的文件夹只是一个普通的、无法进行其他git操作的文件夹。之后,随便新建并写入一个文件(假设它名字叫readne.md。用git add readme.md告诉git你加了这个文件。最后用git commit -m "改动信息"来让git把加的文件给记录下来。
我学到这里的时候十分疑惑:为什么要先add,再commit才能把文件记录下来。为什么不一次性把文件记录下来呢?听说还有个叫github的东西,我’commit’完,还要再进行一步操作才能把文件传到github上面。为什么我想在网上存一份文件要这么多步操作啊!
这里,考虑到知道git的人都知道github,而对git操作有着许多的疑惑,我打算用一张简单的数据流图(该图及后文的称呼并不严谨,仅供学习理解)来介绍git、github的关系,以便于接下来的理解。git与github的具体关系还是放到后面介绍。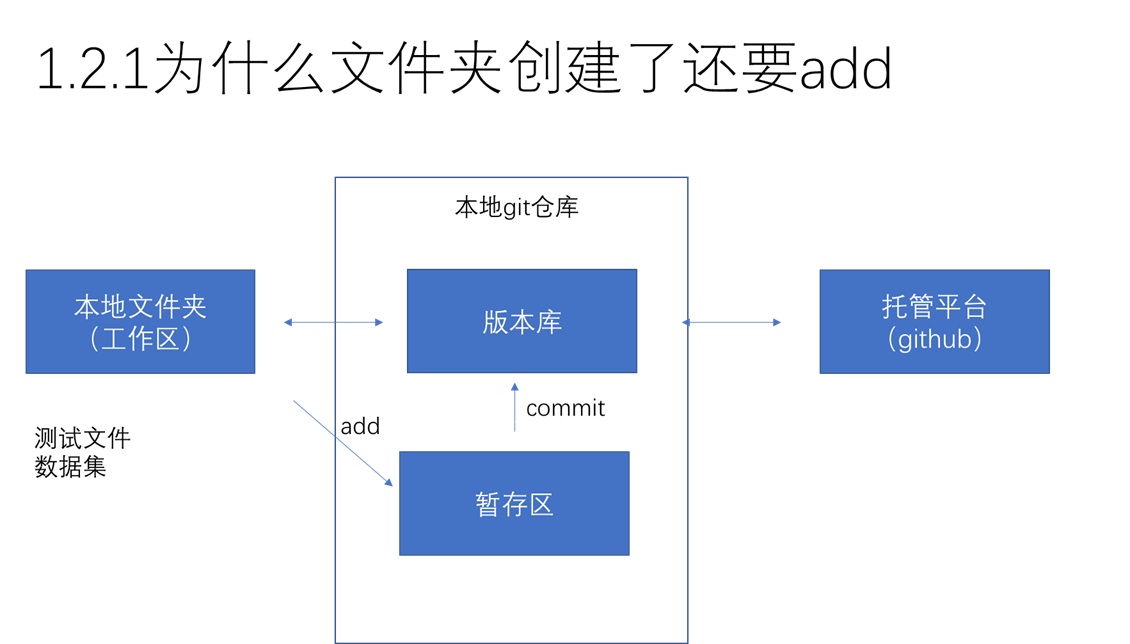
其实啊,git init这条语句看上去没干什么,实际上在你的电脑里新建了一个“文件夹”(逻辑上的,而不是实际的)。这个“文件夹”是本地git仓库。而这个仓库呢,又分成两个分区:暂存区和实际的版本库。可以认为git是一个管家,add进缓存区,就是叫管家把事情记在脑子里;commit进版本库,就是叫管家用水笔把事情记在本子上——这样这条记录就确实储存下来,不好销毁了。那么,使用add把文件放入暂存区的好处就显而易见了:有的时候我们要改/加的文件很可能出错,我们再提交之前,需要把文件检查一遍,这样出了错就能及时更改。一旦文件commit了,更改起来就麻烦了,之前的错误记录也难以消除。
而github一类的托管平台,则又可以视为一个文件夹。这些文件夹可以看成是网盘,它们由运营平台提供,以便于你能用互联网在不同设备上访问自己的仓库。目前对于git、github之间的关系,add与commit之间的关系理解到这个程度就行了。
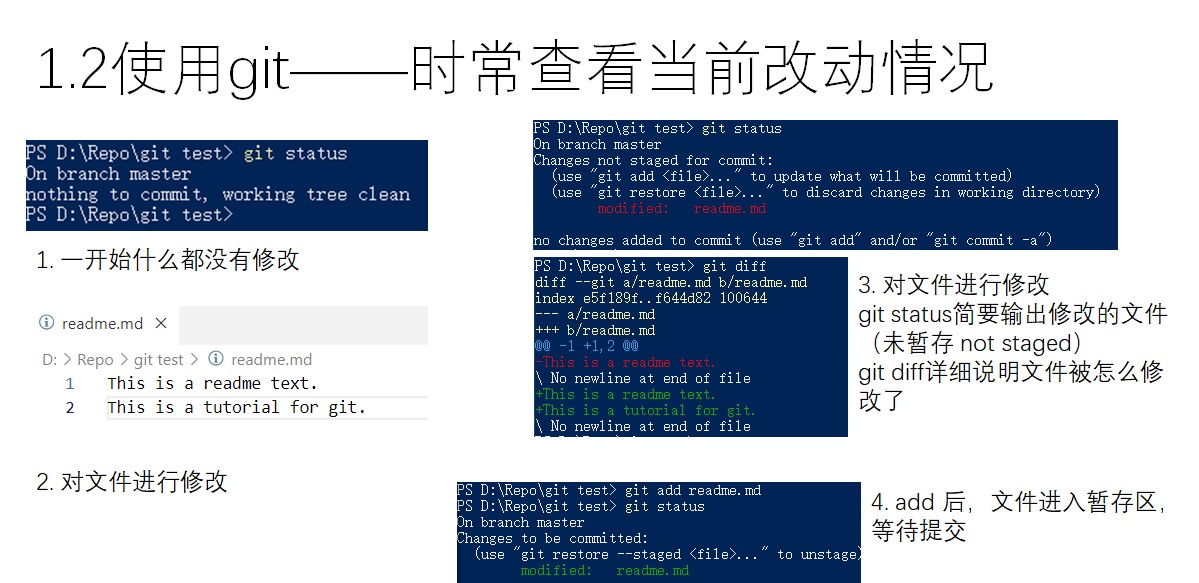
git提供了一个十分使用的命令——git status。该命令不会对git仓库进行任何的修改,而仅仅会输出当前git仓库的状态。如上图所示,修改已有文件,add,commit后,git status都会输出不同的信息。要查看具体的修改细节,可以使用git diff。
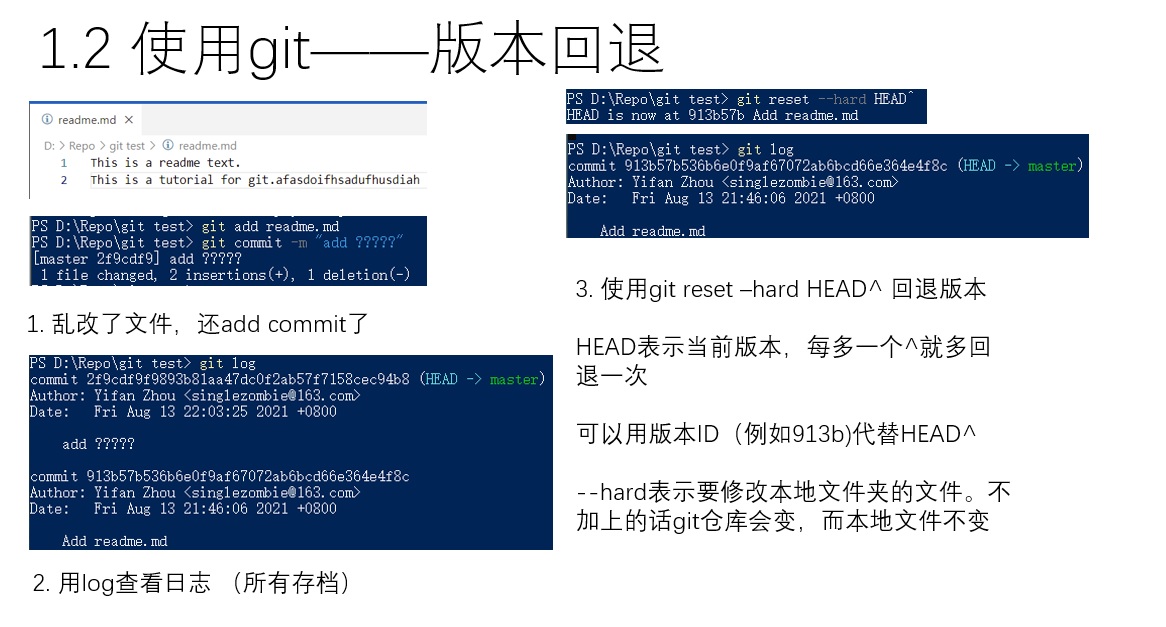
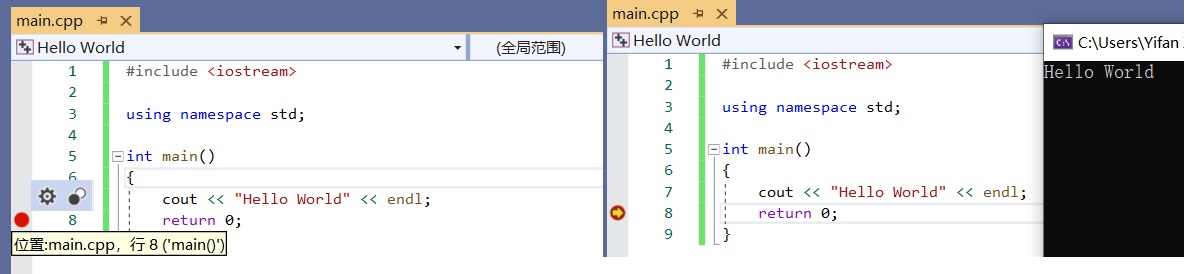
如最开头所说,我们使用版本控制程序的一大原因,就是希望像RPG读档一样,能够让所有文件回到之前某个保存下来的状态中。这样的操作在git中叫做版本回退。上图给出了一个例子,我们不小心在文件里做出了错误的修改,还commit了。这个时候该如何把文件回退呢?
首先,可以使用git log,查看所有提交记录。之后,可以使用git reset --hard <要回退的版本>指令来进行回退。最新的版本叫做HEAD,上一个版本叫做HEAD^,上上个叫做HEADT^^……依次类推,可以快速地回退到上一个版本。除了用这样的方法指定版本号外,还可以用commit的id来指定版本(commit id在log中查找)。指定id的时候不需要把id输全,只需要输入前几位,保证不冲突就行。

除了commit后发现错误想回退,还有一些程度较轻的版本回退情况:不小心修改了文件而没有add,或者已经add了。对于这两种误修改,都有对应的解决情况:如上图所示,如果文件没有add,使用git checkout -- <filename>就可以把对应文件恢复到暂存区的最新状态(最后一次git commit或者git add的状态)。如果文件add了,使用git reset HEAD <filename>就可以把git暂存区中的文件恢复到没有add之前的状态(最后一次git commit的状态),这等于回到了上个问题,文件没有add该怎么恢复。再一次执行git checkout -- <filename>就可以把文件的内容也彻底恢复回去了。
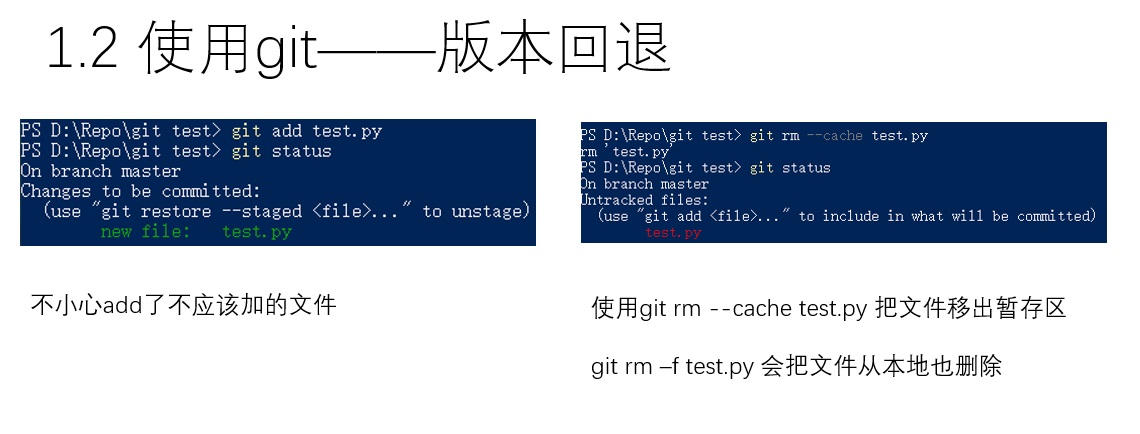
git add是一个很神奇的指令。它的名字虽然叫add,但实际上不管是新建文件、修改文件、还是删除文件,都需要用git add来更新文件在暂存区中的状态。因此,与其叫做add,不如把这个命令称作update比较好。那么,现在问题来了:如上图所示,有一个文件,我不小心让它进入了git暂存区,我想在文件系统里保留它,但不想让它进入git仓库,该怎么操作呢?这个时候就要使用git rm --cache <filename>。这个叫rm的操作是真正意义是上的remove了,而不像add一样有一点歧义。如果想让文件从文件系统中也消失 ,可以用git rm -f <filename>

刚刚我们碰到了这样一个应用场景:有一个文件,我想在文件系统保留它,却不想让它进入git仓库。这些文件可能是我们为了调试而编写的脚本文件,我们不希望这些乱糟糟的文件上传到公开的仓库中。如果我们不做任何处理,每次输入git status都会看到这些在文件夹中存在却没有进入git仓库的untracked files. 该如何让这些碍眼的提示消失呢?这个时候,可以在git仓库的根目录下创建一个.gitignore文件。该文件用于描述不被git跟踪的文件,描述的形式可以是直接描述文件的全名,也可以用*来模糊匹配,还可以直接忽略一整个文件夹。上图的例子中,我们如果在.gitignore中加入test.py,再输入git status就不会提示有文件没有加入git仓库了。
使用github初始化仓库的话,可以自动创建一个.gitignore文件。这个文件也可以参考别人的仓库里的来写。
 讲了这么久的git,终于可以来讲github了。git本身是分布式的,每台电脑都存储了所有的git仓库版本信息。但是,实际上使用的时候,为了在互联网上同步信息,我们一般需要托管平台的帮助。github就是这样一个平台。先直接看一看和github有关的操作吧。
讲了这么久的git,终于可以来讲github了。git本身是分布式的,每台电脑都存储了所有的git仓库版本信息。但是,实际上使用的时候,为了在互联网上同步信息,我们一般需要托管平台的帮助。github就是这样一个平台。先直接看一看和github有关的操作吧。
不管怎么样,所有git操作都是基于一个git仓库。这个git仓库可以是我们本地的,也可以是github上面创建的。
如果本地有了一个仓库,那只需去github上创建一个空的同名仓库,再用图中的第一条命令把远程仓库和本地仓库关联起来。
但是,使用https的方法通信,很容易出现超时的问题。如果之前不小心对https格式的地址进行了绑定,可以先remove掉。

与github关联的正确方式是使用ssh,这是一种更安全高效的连接方式。先像上图一样再本地生成ssh密钥。
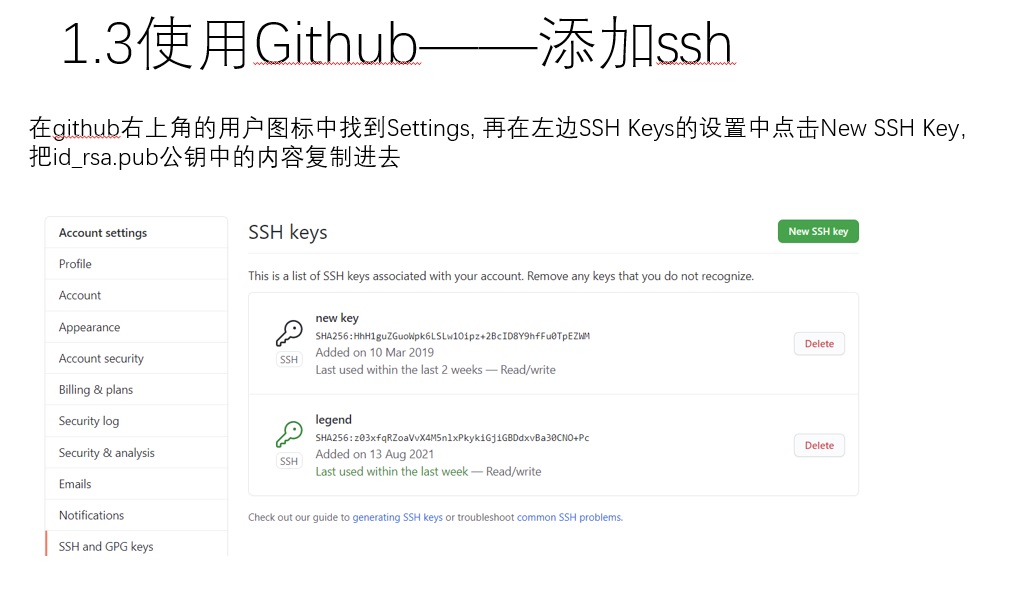
再把公钥放到github上。

这样就可以正常把本地仓库和github的仓库关联起来了。如果本地没有仓库,而是去克隆github上面的仓库,则可以使用git clone指令。
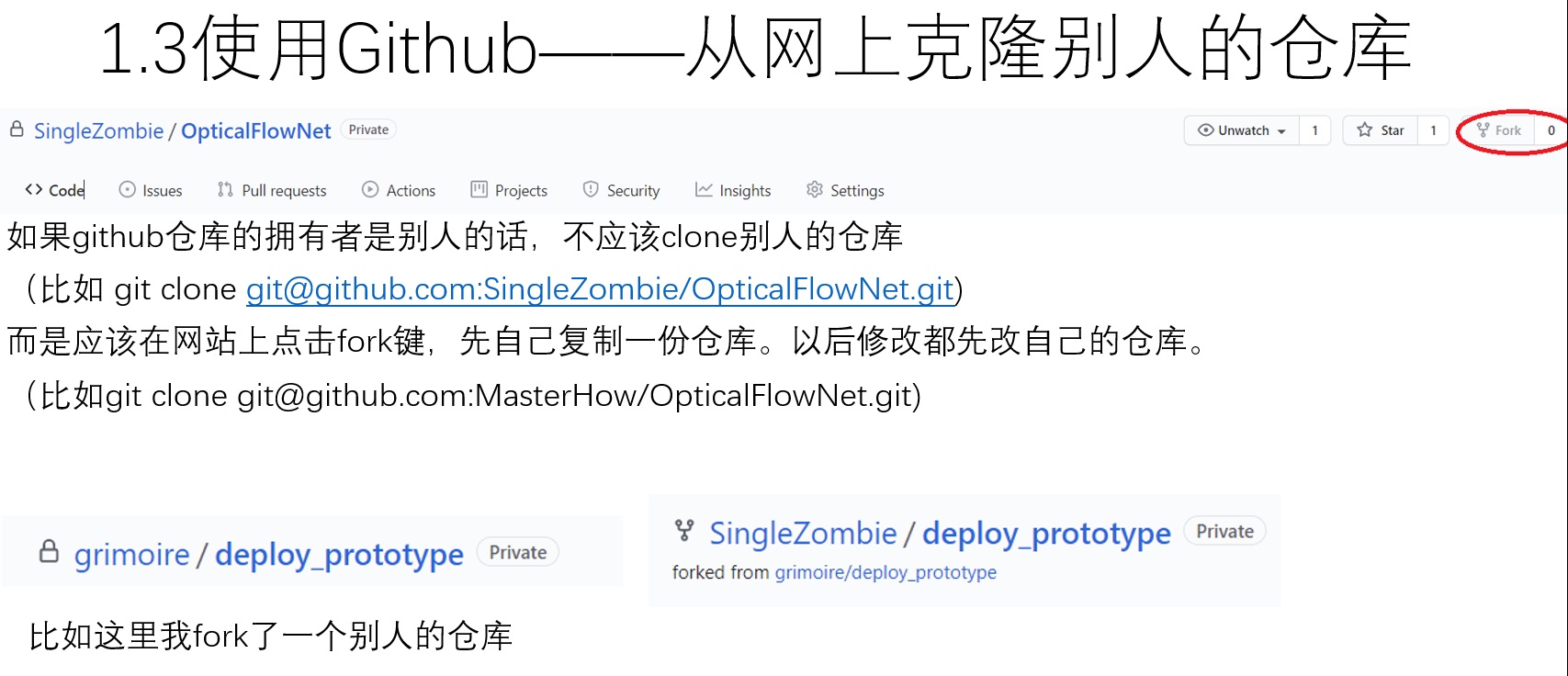
这里特别要说一句。如果只是用别人的代码,clone仓库本身就行了。如果想要对别人的仓库进行贡献,则最好先去github上面点一下fork,分支出一个完全一样的,属于你自己的仓库,再clone这个属于自己的仓库。因为对别人的仓库是无法进行修改等操作的。
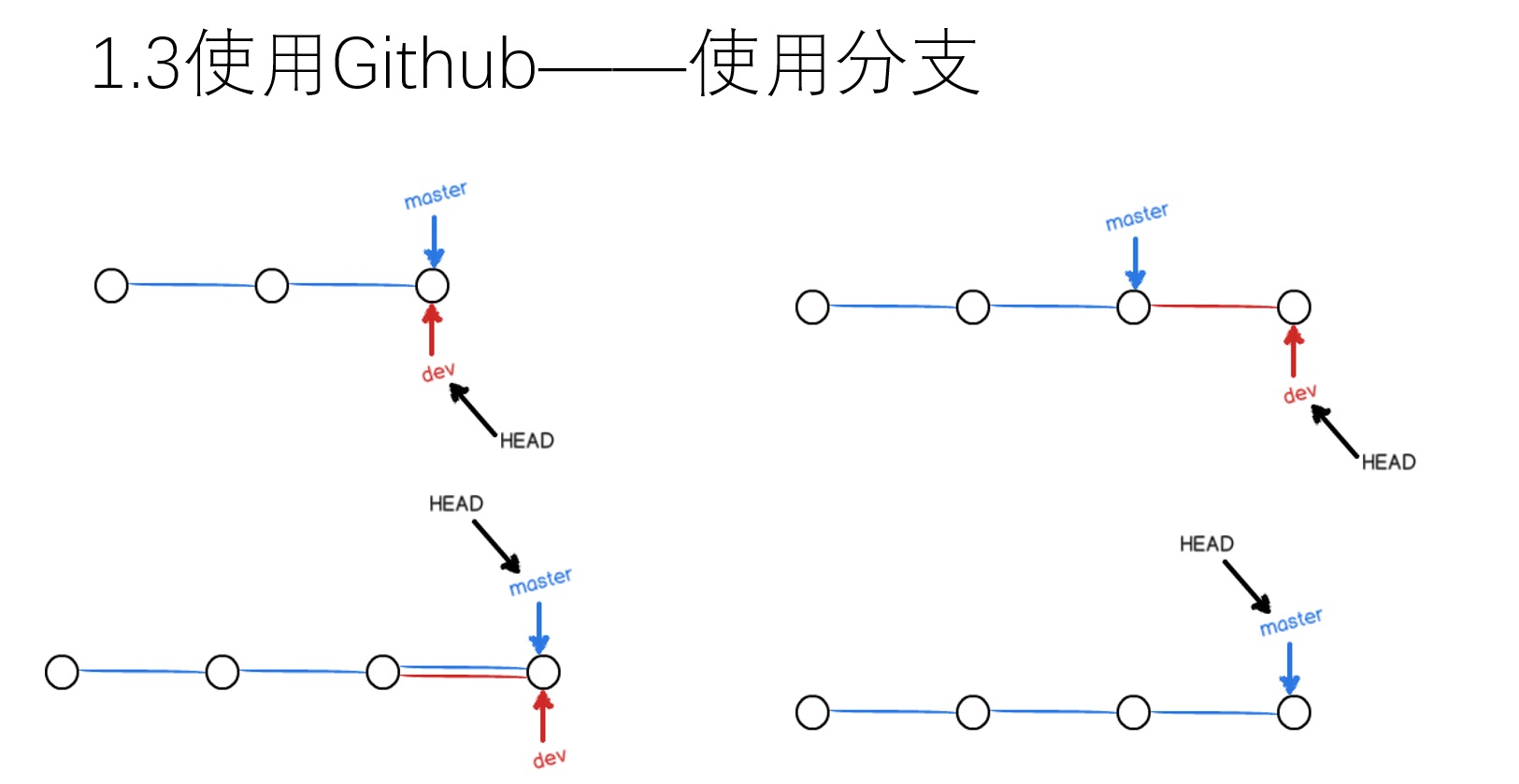
和github的仓库进行关联后,还需要学习一些和分支有关的知识,才能开始使用github。以上图为例,在git里创建分支并在不同的分支开发,就好比在同一台电脑,同一款游戏里,不同的玩家玩到了不同的进度上。当前电脑(HEAD)由玩家dev控制,他玩的进度比较超前。之后轮到玩家master来玩,他看dev的进度很前,于是直接拷贝了dev的游戏存档,这样两个人的游戏进度就完全一样。之后master把dev的存档删了,因为这份存档已经没用了。在这个例子里,两个分支都是线性进行,因此只需要把旧的分支向新分支同步就行。但是,实际开发时,很可能两个分支往不同的方向发展,之后这两个分支还需要进行同步。这个时候就需要对两个分支的信息进行细心的比对,才能把两个分支的代码给融合起来。

开始那副图片描述的内容,可以用上图中的操作来实现。

这页ppt做得不好,它实际包含了两类不太相关的内容:
首先是对开始那些操作的收尾:把副分支向主分支合并后,副分支一般没什么意义了,这个时候可以直接删除。
有了分支的知识,我们就可以理解本地git仓库如何与github上的仓库交互了。我们本地仓库和github上的仓库其实是同一个仓库的两个分支,我们需要不断令这两个仓库同步。
如果本地仓库较新,应该用push,等于是把本地的内容向github上的内容合并。
如果github上的仓库较新,应该用pull,等于把github的内容向本地更新。
这里的命令写得不够具体。理论上两个操作的用法都是git pull/push <remote-repo-name> <branch>这样的格式的。远程仓库名一般叫做origin。但是可以通过--set-upstream可以指定push和pull的默认远程分支。直接git push/pull的时候命令行里会报错,按照提示设置upstream即可。
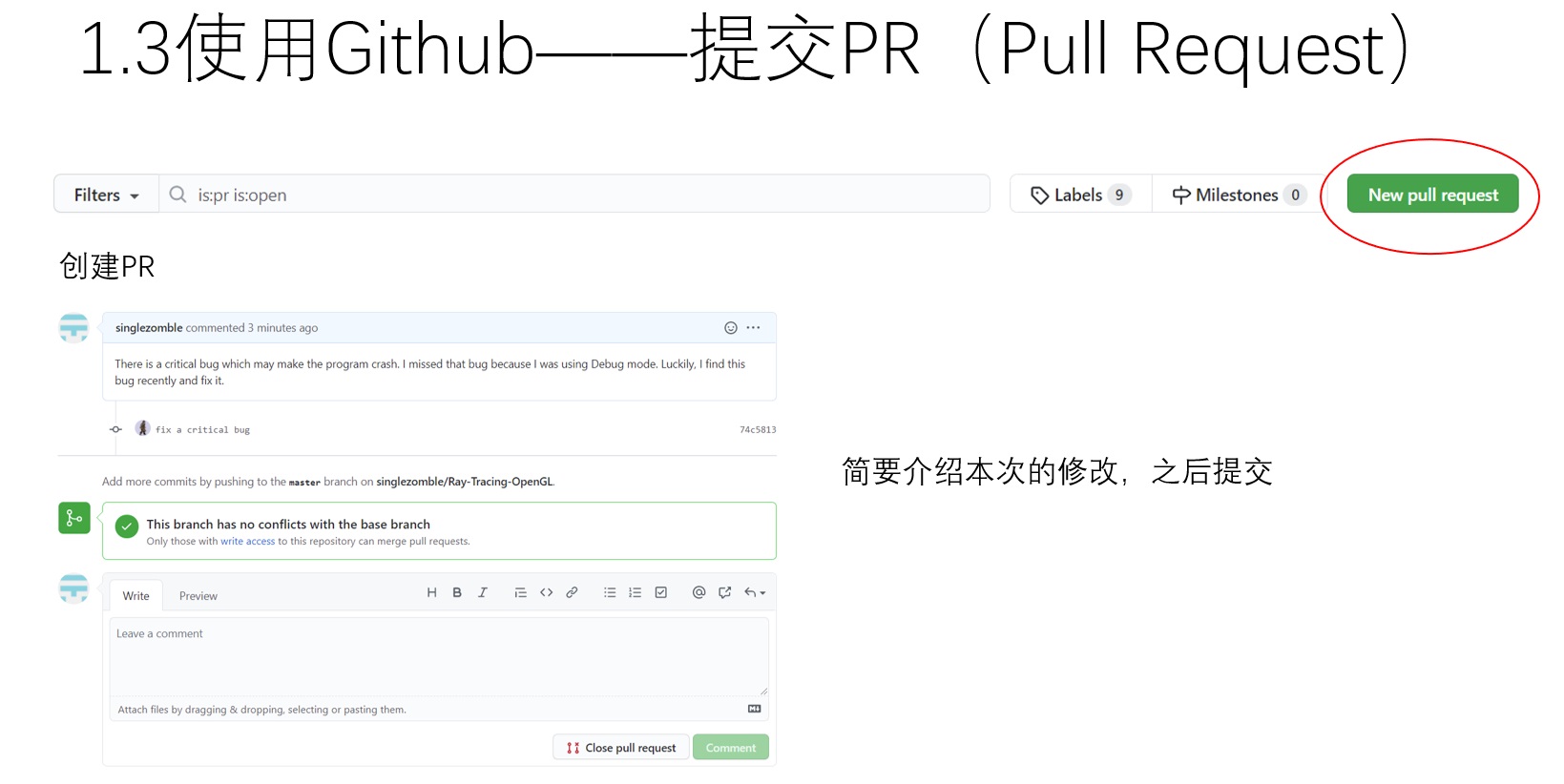
不管是开发自己还是别人的开源项目,都建议创建一个新的分支开发。开发完一项功能后,把新分支推送到github上,再利用github的pull request把分支合并到主分支上。这种开发方式使得在添加新功能时,所有人都能看到哪些代码进行过修改,有利于多人协作。
更新github上的分支的几分钟内,github会主动提示你要不要进行pull request。或者是点击pull request一栏主动进行”New pull request“,都可以开启一个新的PR。
PR的标题和内容一般都有格式要求。如果是向别人贡献代码,一定要向别人的要求对齐。输入完对PR的描述后,就可以正式创建一个PR了。
(这里没截图)PR的审阅者可以在PR的file changes里面查看有哪些代码被修改,确认无误后可以点击approve,并在整个pr的最后面点击merge。这样,一个带有新功能的分支就正式被并入主分支了。
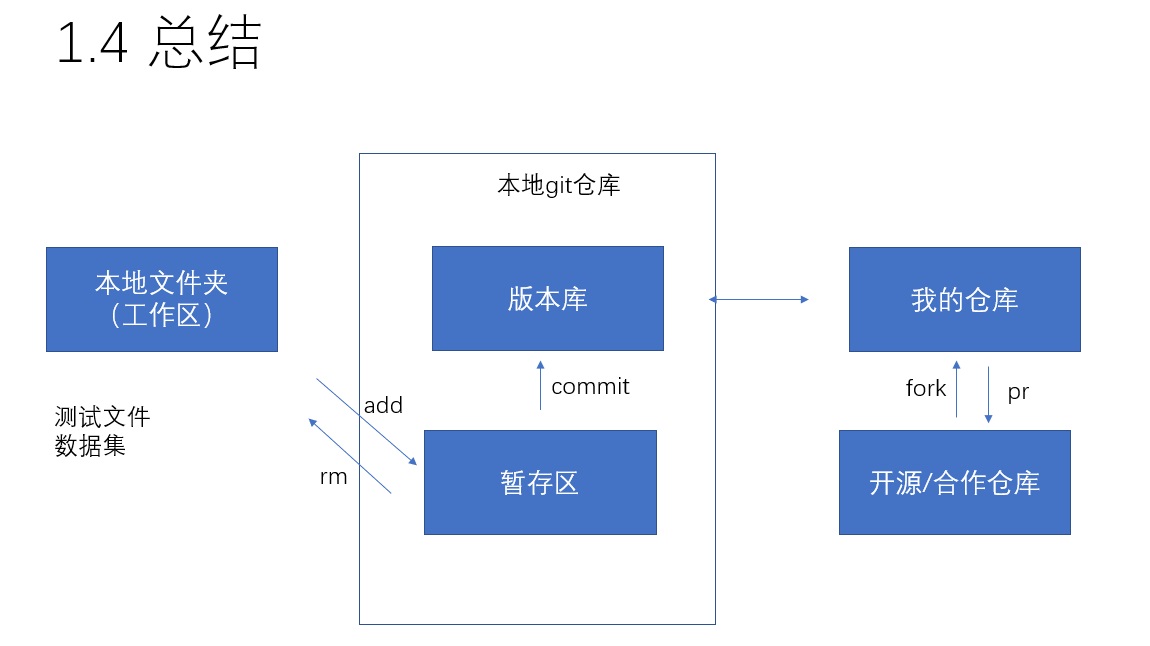
我之前就接触了github,一直用github gui进行个人项目的同步。但是push/pull/commit等概念一直没有弄明白。通过这次彻底的学习后,我建立起了git及github的知识框架,才算是彻底理解了这些工具的使用方法。这个知识框架可以总结为上图。如果一个人学完git的相关知识后,能在脑中建立起类似上图这样的数据流图,那么就可以说是基本理解了git什么多命令究竟是在干什么。
首先,要理解先得存在本地git仓库,在线github的git仓库才有意义。通过add命令,可以把文件夹里的文件托付给git系统进行管理;通过commit命令,可以让git把当前的内容”存档“。
为了使用github,需要把本地仓库和远程仓库关联。如果是从现有的远程仓库开始构建代码,则用git clone;如果是本地仓库已经有了代码,仅需用git remote add关联起远程仓库。后续所有的git pull/push操作都是在同步本地和远程的git仓库分支。
为了对别人的代码进行贡献,需要fork别人的仓库,形成一个自己的仓库。对自己的仓库进行更新后,再以pr的形式请求更新别人的仓库。但开发个人/私有项目时,也建议使用pr的形式更新代码。
git的笔记差不多就这么多。还有很多知识没有在笔记里提及。比如如果合并存在冲突的代码。其实在有了整体的概念后,这些细枝末节的知识反而都很好理解了。
我反正在学完了git的基础知识后,就再也不用命令行,而是用一些其他工具来进行git仓库的管理了。我现在在使用vscode的git管理系统。里面add、commit都可以方便地进行操作。冲突合并也就是点一点按钮的事情。
我的博客的分类/标签管理方法
之前我把博客里所有博文的分类、标签进行了重构,一直没有提及。这里简要介绍一下重构的内容,及重构后分类和标签的使用依据。
之前的分类和标签貌似是英文。我也不知道自己怎么想的。既然博客的内容全是中文,那么读者也全是会中文的人,用英文的分类/标签没什么意义。当然,我是发现自己想给新分类取名,却怎么也不知道如何用英文来表达某个中文词语的意思时,才准备把所有分类/标签改成中文的。
现在的分类是按照文章的性质进行分类。目前分类仅有两级,直觉上分三级可能更好一点,不知道以后还有没有改进的空间。
目前有学习/杂谈/经验分享/记录这几大类。”学习“就是分享一些客观正确的事情。”工具用法指南“包括软件的安装使用方法,这些是最没有技术含量、原创性,最死板的内容‘;”知识“是我对某一学科的知识的再表达,主要是巩固我自己的学习,内容有一定的原创性,但根本目的还是复述别人的知识,这个名字取得不好,改成”知识分享“或许更合理一点;这篇文章所属的”学习笔记“可以说是劣化版的”知识分享“,原创性稍高一点,但完成度低,内容连贯性差,不适合作为第一手学习资料,适合作为参考,或者用于我口头讲授的素材。
”杂谈“就是中小学生作文。有的文章是有一些深意的,有的文章是随便写的,”趣文“里的就真的是写来玩的。
”经验分享“和”杂谈“一样,是原创性极强的作品,主要是我个人的见解。但提出系统性的个人见解非常困难,还需要保证不与客观事实或参考资料有出入,目前文章较少。”经验分享“这个名字也不是很恰当。说不定以后”经验分享“专门来放一点原创性强,但是不够有深度和完成度,随便写的一些经验分享文章。专门开一个”我的理论“来放最具原创性和深度的文章。
”记录“里包含了专门对我完成的某件事做描述的文章。这里有些东西是为了好玩而写,有些东西是为了丰富个人简历,专门写给别人看的。
分类只能给所有文章从性质这一个维度上进行一个大概的分类,但我感觉用标签检索文章更加合适。标签比分类更加灵活,可以像分类一样描述文章性质(日记),也可以描述文章涉及的内容(数学),还可以标识一类专题(未来可能出现的”博士毕业论文“)。目前标签我是想到什么放什么。
用标签的时候会有一个问题:理论上标签越多越好,但是如果某一天突然想出一个新标签,但以前有些文章可以套入这个标签,却还没有加,我该怎么给以前的文章加标签呢?或者说我想出了一个新标签,却忘了以前想出了类似的标签,取了个不同的名字,这样标签该如何对齐呢?感觉标签使用起来非常麻烦。一个简单的方法是怠惰处理,以前的内容不管了,只管现在和未来的标签是正确的。
写这篇学习笔记的感想
确切来说,要分成对”学习笔记“的感想和对写这篇文章的感想。
我之前一直不肯写学习笔记。一个人真要学会一个东西,不一定要像”学霸“一样记下花花绿绿的笔记,只需要在关键处进行顿悟式的理解,再在脑中建立知识框架即可。在学一个东西的时候(尤其是学习需逻辑思考而非记忆事实的知识),很可能什么都不用记,或者只是对关键知识进行了演算或者分析,留下一些草稿。记录笔记,其实应该是一个向他人表达知识的过程,应该把这个过程用于巩固知识的理解。在这一过程中,把问题讲清楚一般是十分困难的,因为我们的大脑此时都用于如何让脑中的知识变通顺,而无暇顾及他人能否理解我们在讲什么。只有完全学懂了,才可能写出漂亮的笔记或教程;若是对知识的理解更高一层,才可以写教材。我之前一直认为我写的学习笔记没用,因为这些学习笔记属于我个人学习的副产品——正如我们呼出的二氧化碳一样。要把它们转换成能给人看的东西,需要花很多心血。我自己学东西的时候,经常去网上查资料,总能查到这样的一些学习笔记:这些学习笔记缺乏逻辑性,完全不能用来进行自学,看它们就是在浪费时间。我不希望自己的发出来的学习笔记干扰他人的学习。但最近我开始愿意发出自己写的学习笔记了。
这里再次强调一遍学习笔记所属的性质。我之前”知识“(未来将改成”知识分享“)中的文章,是以现有教材为素材,记录我个人分析与总结的文章;而学习笔记,则应该算是自己写出来的学习素材,我加上了一些描述以使得它们勉强可读。这两类文章本质上来说都是我自学的时候用的。
现在开始讲我愿意发学习笔记的原因。首先是因为最近我有分享知识的需要,制造了一些用于讲授的学习素材。这些素材只要加工一下就能发出来让别人看了。有了积累,不发表出来,实在太亏了。我是不愿亏的人,很想有了东西就发表出来。
发学习笔记的最大问题是需要加入一些描述性的文字。写这篇学习笔记之前,我的想法是随便写点文字描述一下就得了。但是,写着写着,我发现不多写点字是不可能把抽象的知识描述清楚的。最后,我只好在文章质量上进行妥协。文字优美与否、通顺与否我已经关心不了了,我只能尽可能让文章可读,并且赶快把文章写完。赶快做出了一个能用的东西,比憋半天什么都做不出来要好。
我之前不想发学习笔记的另一个原因是,我把学习笔记和教材搞混了。教材需要对知识进行面面俱到而精准无误的描述。这样的工作量的巨大的。现在我想通了:学习笔记就是参考资料,我也强烈建议读者不要把学习笔记当成自学的资料来用。学了一会儿,或者知识掌握得已经差不多后,再来以批判的眼光看学习笔记,哪里写得好,哪里有疏漏。这样看待学习笔记才是对的。
再吐槽一下写这篇文章的感想。
我讲这几页ppt的时候感觉十分轻松。我感觉随便写点内容就能把ppt串起来了。但实际写文章的时候却不是这样的,我感觉ppt缺斤少两,逻辑混乱,得加大量的文字才能把话说清楚。最后,我花了比预计多得多的时间才把这篇博文完成。
可见,基于语音的授课的教学效果还是很好的。加上答疑机制的存在,理想情况下教师能够把要讲的知识完全传授给学生。只要学生稍微会学习,老师有强大的表达能力,就能把知识通过上课这种方法传授出去。可惜,大部分人不会教学,逼得学生通过阅读的方式自学。阅读式学习对教授者和学生的要求都更高。真的要感谢那些写出优秀教程/教材的人。
再对我自己和读者强调一句:凡是以实践为目标的技术,一定要在实践中学习,不然学不进去。我们从小到大写那么多作业,就是为了利用实践来加强对知识的理解。对于一种编程技术,学习并验证学习情况的最好方法就是把这个技术用出去。
写这篇学习笔记太累了。如果还要保持产出,我只能进一步降低学习笔记的文章质量了。
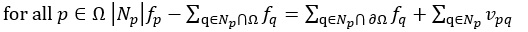





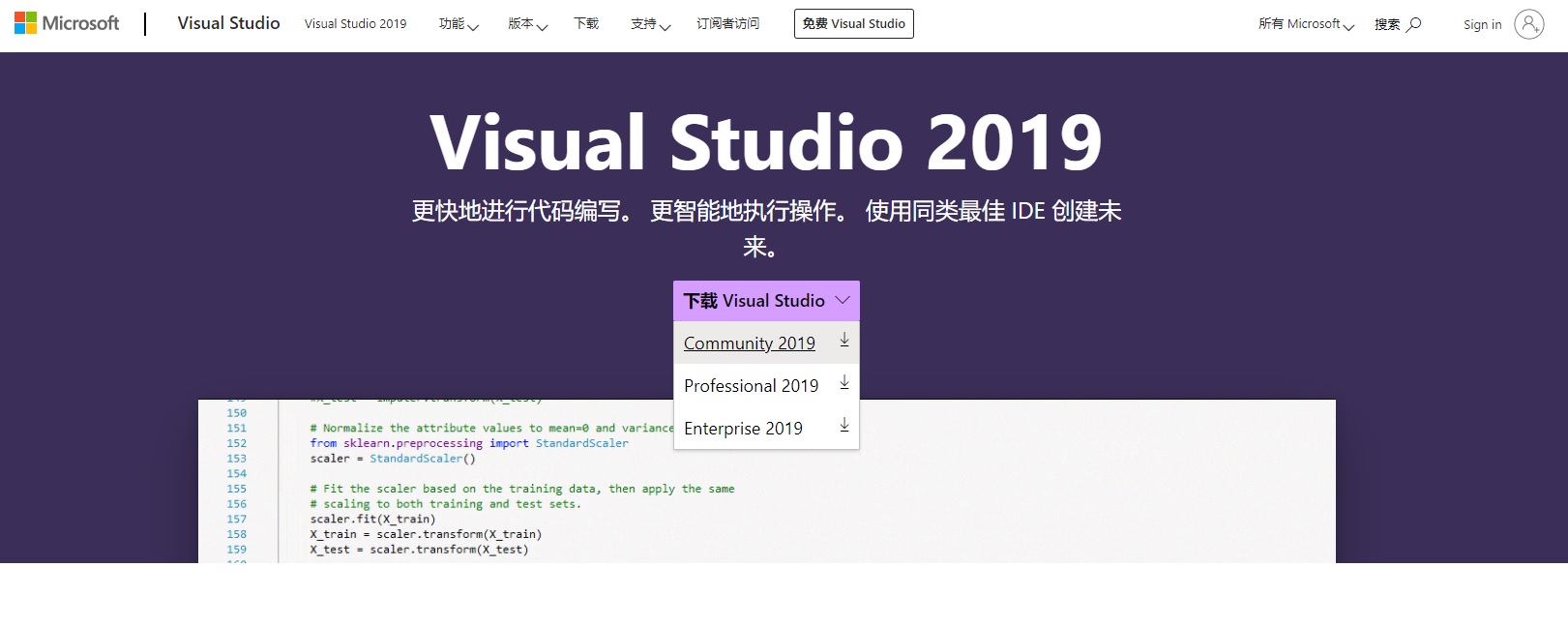
 下载很快就会结束。规模这么庞大的编程软件,几分钟就下载完了?其实我们现在只下载了一个下载器,待会才会正式开始下载VS的本体。
下载很快就会结束。规模这么庞大的编程软件,几分钟就下载完了?其实我们现在只下载了一个下载器,待会才会正式开始下载VS的本体。
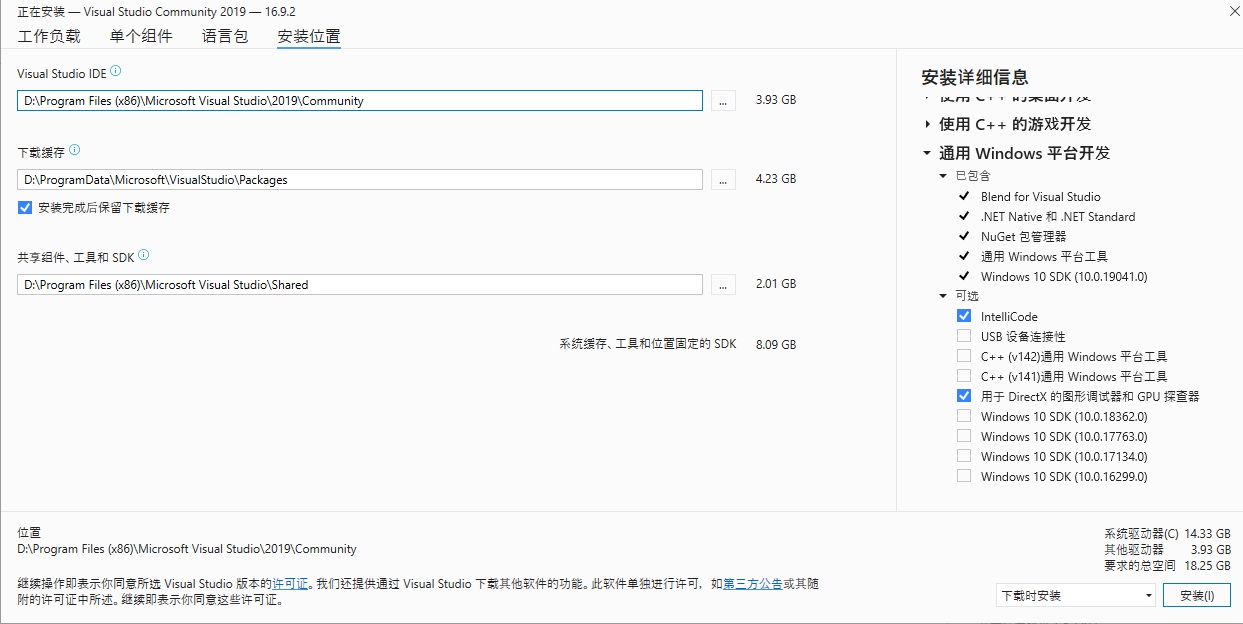
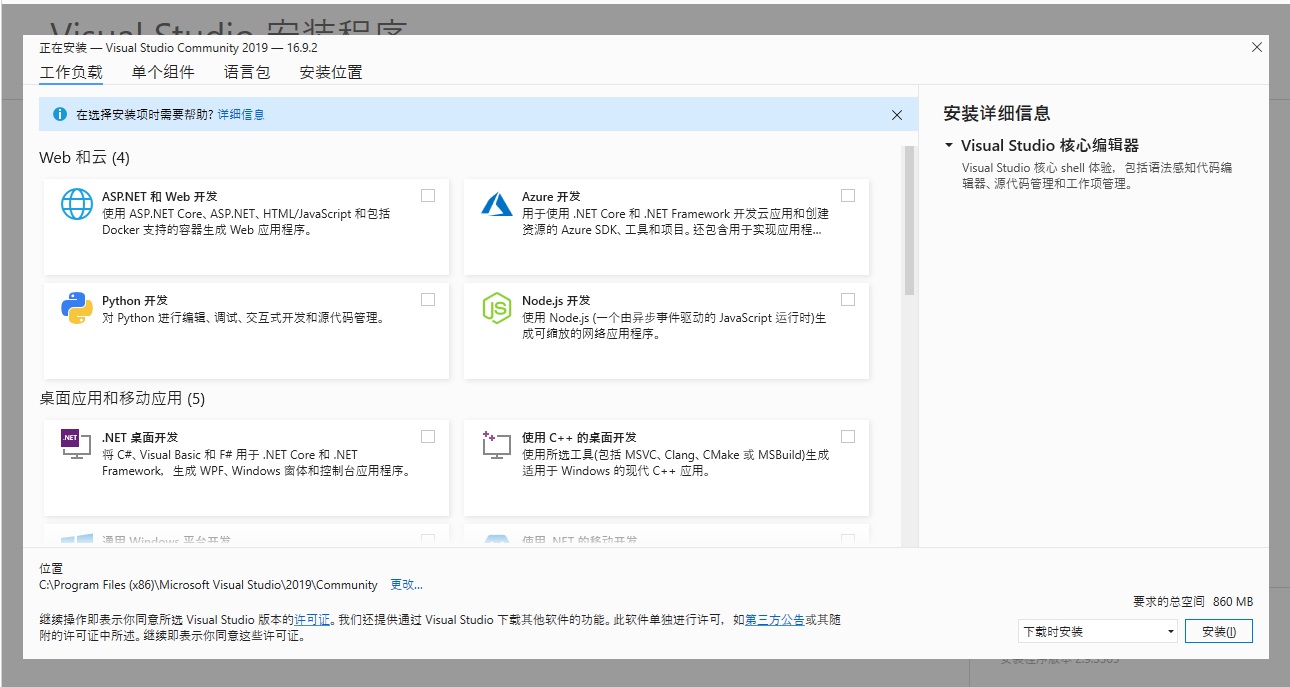 刚看到这个界面,第一次用VS的人肯定会有点懵:哎呀!怎么这么多选项啊!该点哪个呀?
刚看到这个界面,第一次用VS的人肯定会有点懵:哎呀!怎么这么多选项啊!该点哪个呀?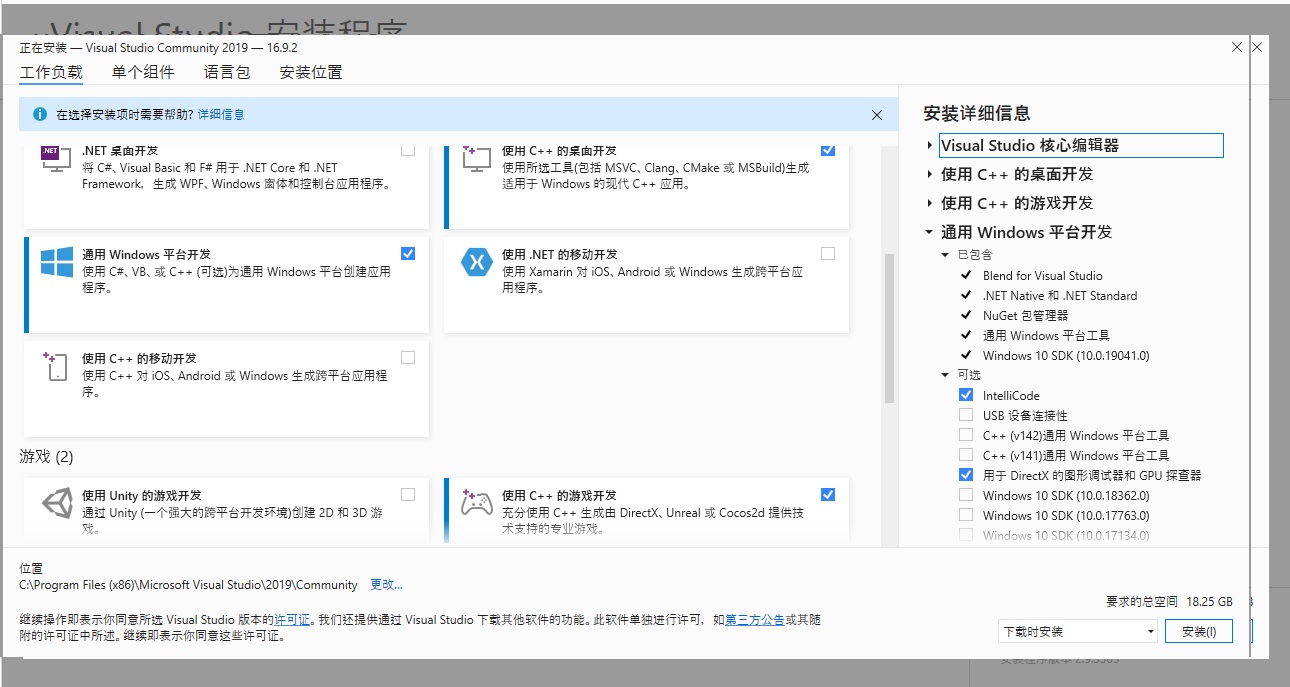 所以,我们应该根据自己的需要选择要开发的语言。只进行C++的开发的话,只点击”使用C++的桌面开发“即可。上图中,我多点了几个选项。
所以,我们应该根据自己的需要选择要开发的语言。只进行C++的开发的话,只点击”使用C++的桌面开发“即可。上图中,我多点了几个选项。